Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 115508 by bemath last updated on 26/Sep/20

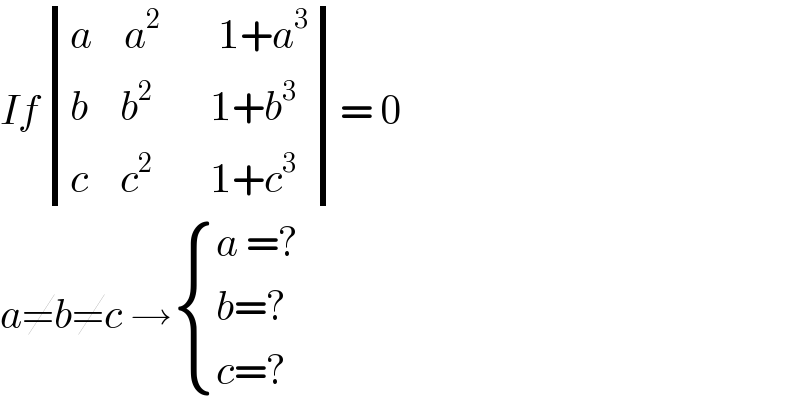
If determinant (((a a^2 1+a^3 )),((b b^2 1+b^3 )),((c c^2 1+c^3 )))= 0 a≠b≠c → { ((a =?)),((b=? )),((c=?)) :}

$${If}\begin{vmatrix}{{a}\:\:\:\:{a}^{\mathrm{2}} \:\:\:\:\:\:\:\mathrm{1}+{a}^{\mathrm{3}} }\\{{b}\:\:\:\:{b}^{\mathrm{2}} \:\:\:\:\:\:\:\mathrm{1}+{b}^{\mathrm{3}} }\\{{c}\:\:\:\:{c}^{\mathrm{2}} \:\:\:\:\:\:\:\mathrm{1}+{c}^{\mathrm{3}} }\end{vmatrix}=\:\mathrm{0} \\ $$$${a}\neq{b}\neq{c}\:\rightarrow\begin{cases}{{a}\:=?}\\{{b}=?\:}\\{{c}=?}\end{cases} \\ $$

Answered by bobhans last updated on 26/Sep/20

⇒ determinant (((a a^2 1)),((b b^2 1)),((c c^2 1)))+ determinant (((a a^2 a^3 )),((b b^2 b^3 )),((c c^2 c^3 )))= 0 ⇒(−1) determinant (((1 a^2 a)),((1 b^2 b)),((1 c^2 c)))+ abc determinant (((1 a a^2 )),((1 b b^2 )),((1 c c^2 )))= 0 ⇒(−1)^2 determinant (((1 a a^2 )),((1 b b^2 )),((1 c c^2 )))+ abc determinant (((1 a a^2 )),((1 b b^2 )),((1 c c^2 )))= 0 ⇒(1+abc) determinant (((1 a a^2 )),((1 b b^2 )),((1 c c^2 )))= 0 ⇒(1+abc) determinant (((1 a a^2 )),((0 b−a b^2 −a^2 )),((0 c−a c^2 −a^2 )))= 0 ⇒(1+abc) determinant (((b−a b^2 −a^2 )),((c−a c^2 −a^2 )))= 0 ⇒(1+abc)[(b−a)(c−a)(c+a)−(c−a)(b−a)(b+a)]=0 ⇒(1+abc)(b−a)(c−a) [ c+a−b−a] = 0 (1+abc)(b−a)(c−a)(c−b) = 0 since a≠b≠c ; so we get abc = −1 let a = k , b = l → c = −(1/(k.l))

$$\Rightarrow\begin{vmatrix}{{a}\:\:\:\:{a}^{\mathrm{2}} \:\:\:\:\mathrm{1}}\\{{b}\:\:\:\:{b}^{\mathrm{2}} \:\:\:\:\mathrm{1}}\\{{c}\:\:\:\:{c}^{\mathrm{2}} \:\:\:\:\mathrm{1}}\end{vmatrix}+\:\begin{vmatrix}{{a}\:\:\:{a}^{\mathrm{2}} \:\:\:\:{a}^{\mathrm{3}} }\\{{b}\:\:\:\:{b}^{\mathrm{2}} \:\:\:{b}^{\mathrm{3}} \:}\\{{c}\:\:\:\:{c}^{\mathrm{2}} \:\:\:{c}^{\mathrm{3}} }\end{vmatrix}=\:\mathrm{0} \\ $$$$\Rightarrow\left(−\mathrm{1}\right)\begin{vmatrix}{\mathrm{1}\:\:\:{a}^{\mathrm{2}} \:\:\:\:{a}}\\{\mathrm{1}\:\:\:{b}^{\mathrm{2}} \:\:\:\:{b}}\\{\mathrm{1}\:\:\:{c}^{\mathrm{2}} \:\:\:{c}}\end{vmatrix}+\:{abc}\begin{vmatrix}{\mathrm{1}\:\:\:{a}\:\:\:{a}^{\mathrm{2}} }\\{\mathrm{1}\:\:\:{b}\:\:\:\:{b}^{\mathrm{2}} }\\{\mathrm{1}\:\:\:{c}\:\:\:{c}^{\mathrm{2}} }\end{vmatrix}=\:\mathrm{0} \\ $$$$\Rightarrow\left(−\mathrm{1}\right)^{\mathrm{2}} \begin{vmatrix}{\mathrm{1}\:\:\:\:{a}\:\:\:\:{a}^{\mathrm{2}} }\\{\mathrm{1}\:\:\:\:{b}\:\:\:\:\:{b}^{\mathrm{2}} }\\{\mathrm{1}\:\:\:\:{c}\:\:\:\:{c}^{\mathrm{2}} }\end{vmatrix}+\:{abc}\:\begin{vmatrix}{\mathrm{1}\:\:\:\:{a}\:\:\:\:{a}^{\mathrm{2}} }\\{\mathrm{1}\:\:\:\:{b}\:\:\:\:\:{b}^{\mathrm{2}} }\\{\mathrm{1}\:\:\:\:{c}\:\:\:\:\:{c}^{\mathrm{2}} }\end{vmatrix}=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+{abc}\right)\:\begin{vmatrix}{\mathrm{1}\:\:\:\:{a}\:\:\:\:{a}^{\mathrm{2}} }\\{\mathrm{1}\:\:\:\:{b}\:\:\:\:{b}^{\mathrm{2}} }\\{\mathrm{1}\:\:\:\:{c}\:\:\:\:{c}^{\mathrm{2}} }\end{vmatrix}=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+{abc}\right)\:\begin{vmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:{a}\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} }\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:{b}−{a}\:\:\:\:{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }\\{\mathrm{0}\:\:\:\:\:\:\:\:\:{c}−{a}\:\:\:\:\:{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }\end{vmatrix}=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+{abc}\right)\:\begin{vmatrix}{{b}−{a}\:\:\:\:\:\:\:\:{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }\\{{c}−{a}\:\:\:\:\:\:\:{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }\end{vmatrix}=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+{abc}\right)\left[\left({b}−{a}\right)\left({c}−{a}\right)\left({c}+{a}\right)−\left({c}−{a}\right)\left({b}−{a}\right)\left({b}+{a}\right)\right]=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+{abc}\right)\left({b}−{a}\right)\left({c}−{a}\right)\:\left[\:{c}+{a}−{b}−{a}\right]\:=\:\mathrm{0} \\ $$$$\left(\mathrm{1}+{abc}\right)\left({b}−{a}\right)\left({c}−{a}\right)\left({c}−{b}\right)\:=\:\mathrm{0}\: \\ $$$${since}\:{a}\neq{b}\neq{c}\:;\:{so}\:{we}\:{get}\:{abc}\:=\:−\mathrm{1}\: \\ $$$${let}\:{a}\:=\:{k}\:,\:{b}\:=\:{l}\:\rightarrow\:{c}\:=\:−\frac{\mathrm{1}}{{k}.{l}} \\ $$$$ \\ $$

Commented by bemath last updated on 26/Sep/20

gave kudos

$${gave}\:{kudos} \\ $$

Answered by TANMAY PANACEA last updated on 26/Sep/20

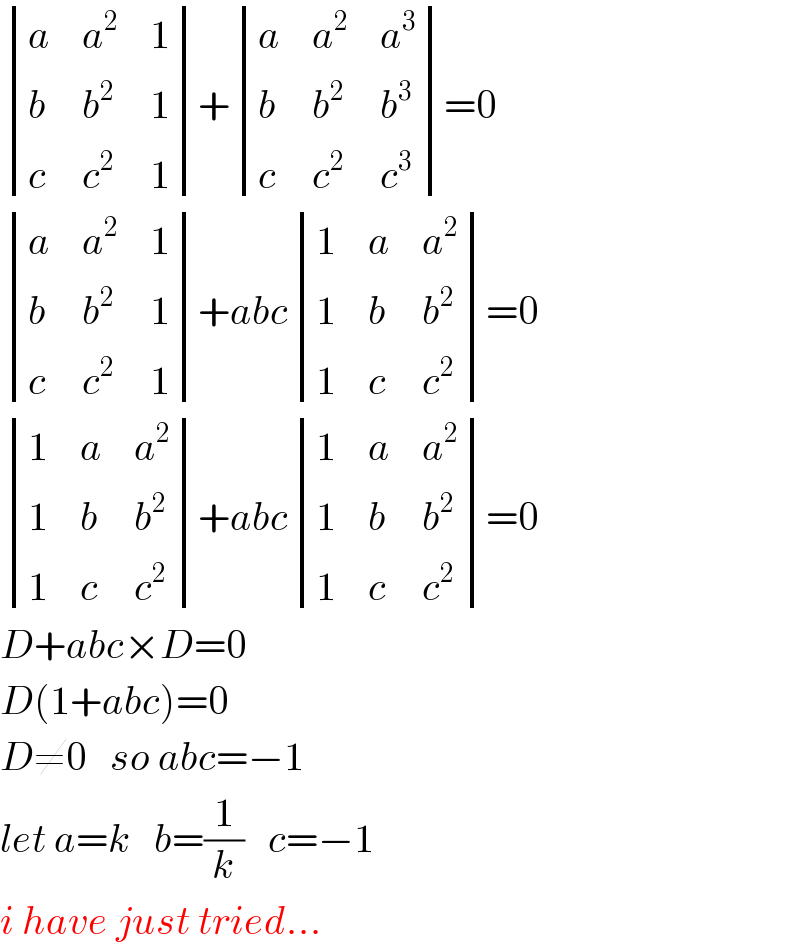
determinant ((a,a^2 ,1),(b,b^2 ,1),(c,c^2 ,1))+ determinant ((a,a^2 ,a^3 ),(b,b^2 ,b^3 ),(c,c^2 ,c^3 ))=0 determinant ((a,a^2 ,1),(b,b^2 ,1),(c,c^2 ,1))+abc determinant ((1,a,a^2 ),(1,b,b^2 ),(1,c,c^2 ))=0 determinant ((1,a,a^2 ),(1,b,b^2 ),(1,c,c^2 ))+abc determinant ((1,a,a^2 ),(1,b,b^2 ),(1,c,c^2 ))=0 D+abc×D=0 D(1+abc)=0 D≠0 so abc=−1 let a=k b=(1/k) c=−1 i have just tried...

$$\begin{vmatrix}{{a}}&{{a}^{\mathrm{2}} }&{\mathrm{1}}\\{{b}}&{{b}^{\mathrm{2}} }&{\mathrm{1}}\\{{c}}&{{c}^{\mathrm{2}} }&{\mathrm{1}}\end{vmatrix}+\begin{vmatrix}{{a}}&{{a}^{\mathrm{2}} }&{{a}^{\mathrm{3}} }\\{{b}}&{{b}^{\mathrm{2}} }&{{b}^{\mathrm{3}} }\\{{c}}&{{c}^{\mathrm{2}} }&{{c}^{\mathrm{3}} }\end{vmatrix}=\mathrm{0} \\ $$$$\begin{vmatrix}{{a}}&{{a}^{\mathrm{2}} }&{\mathrm{1}}\\{{b}}&{{b}^{\mathrm{2}} }&{\mathrm{1}}\\{{c}}&{{c}^{\mathrm{2}} }&{\mathrm{1}}\end{vmatrix}+{abc}\begin{vmatrix}{\mathrm{1}}&{{a}}&{{a}^{\mathrm{2}} }\\{\mathrm{1}}&{{b}}&{{b}^{\mathrm{2}} }\\{\mathrm{1}}&{{c}}&{{c}^{\mathrm{2}} }\end{vmatrix}=\mathrm{0} \\ $$$$\begin{vmatrix}{\mathrm{1}}&{{a}}&{{a}^{\mathrm{2}} }\\{\mathrm{1}}&{{b}}&{{b}^{\mathrm{2}} }\\{\mathrm{1}}&{{c}}&{{c}^{\mathrm{2}} }\end{vmatrix}+{abc}\begin{vmatrix}{\mathrm{1}}&{{a}}&{{a}^{\mathrm{2}} }\\{\mathrm{1}}&{{b}}&{{b}^{\mathrm{2}} }\\{\mathrm{1}}&{{c}}&{{c}^{\mathrm{2}} }\end{vmatrix}=\mathrm{0} \\ $$$${D}+{abc}×{D}=\mathrm{0} \\ $$$${D}\left(\mathrm{1}+{abc}\right)=\mathrm{0} \\ $$$${D}\neq\mathrm{0}\:\:\:{so}\:{abc}=−\mathrm{1} \\ $$$${let}\:{a}={k}\:\:\:{b}=\frac{\mathrm{1}}{{k}}\:\:\:{c}=−\mathrm{1} \\ $$$${i}\:{have}\:{just}\:{tried}... \\ $$

Commented by bemath last updated on 26/Sep/20

gave kudos sir.

$${gave}\:{kudos}\:{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com