
Question and Answers Forum
Question Number 115541 by bobhans last updated on 26/Sep/20
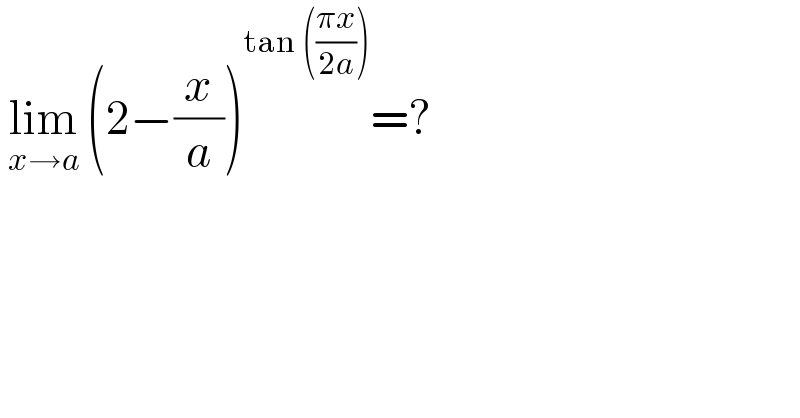
Answered by bemath last updated on 26/Sep/20
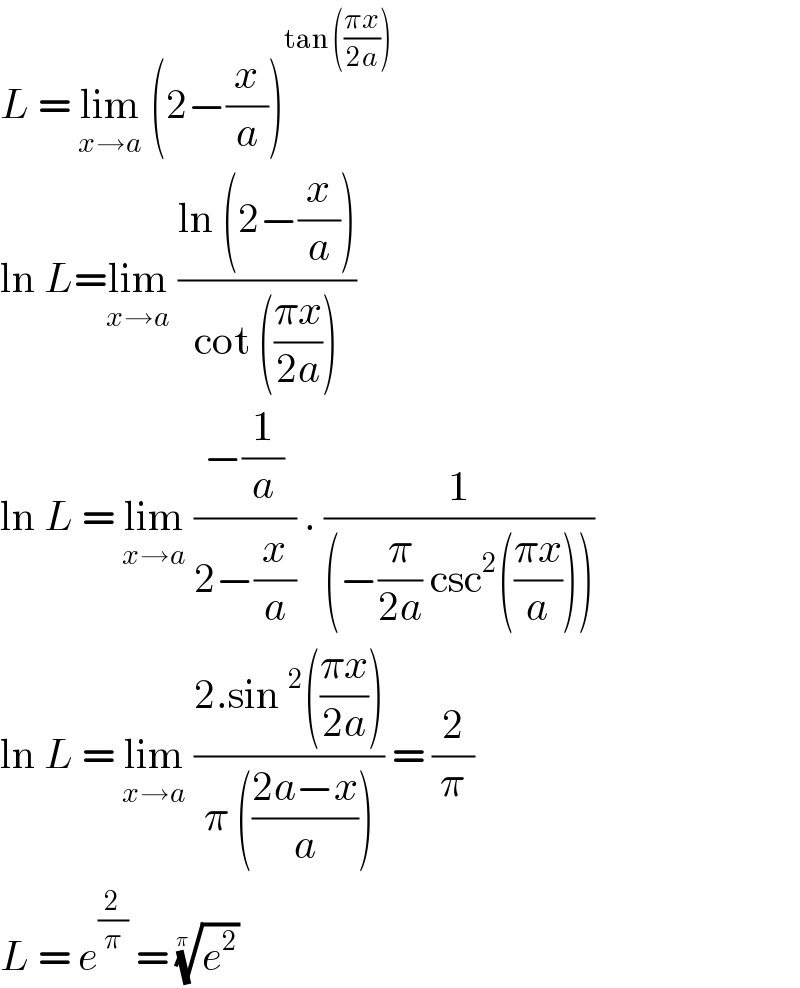
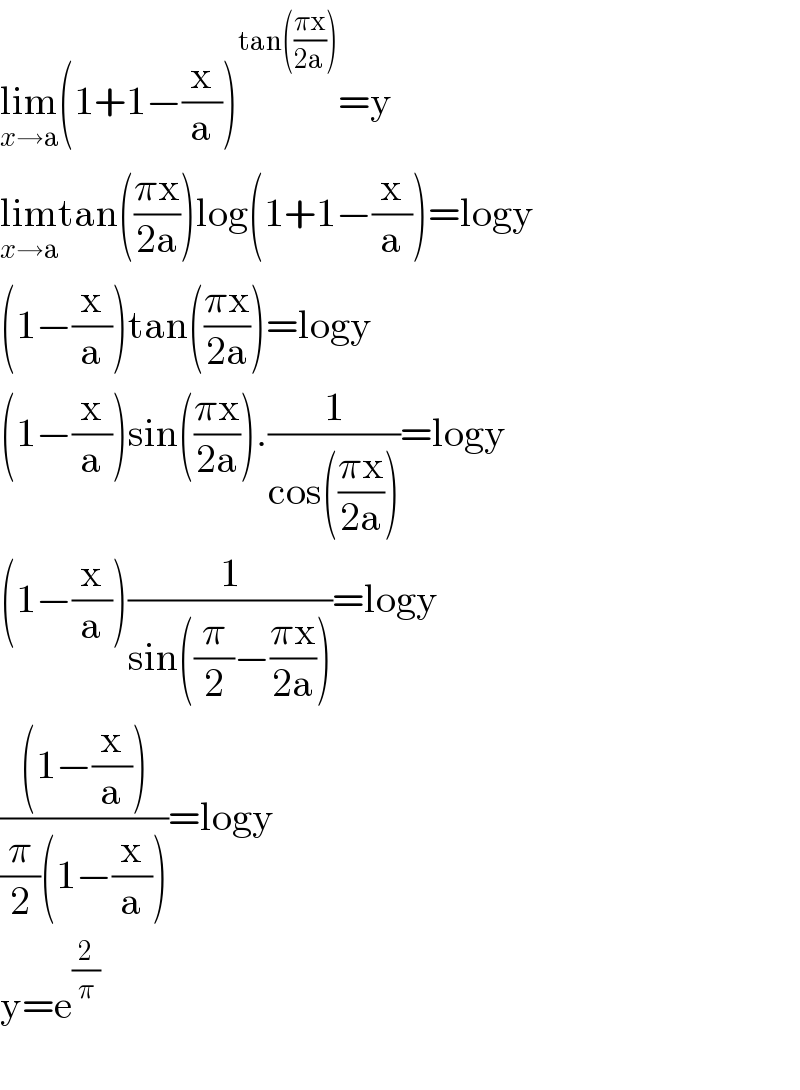
Answered by Dwaipayan Shikari last updated on 26/Sep/20
Answered by mnjuly1970 last updated on 26/Sep/20
![solution: 1−(x/a) =t {_(t→0) ^(x→a) lim_(t→0) (1+t)^(tan[(π/2)(1−t)]) =lim_(t→0 ) (1+t)^(cot((π/2)t)) =_(t→0) ^( sin((π/2)t)∽(π/2)t) lim_(t→0) [((1+t)^(2/π) )^(1/t) ]^(cos((π/2)t)) =_(t→0) ^(cos((π/2)t)→1) =e^(2/π) ✓ m.n.july.1970](Q115553.png)
| ||
Question and Answers Forum | ||
Question Number 115541 by bobhans last updated on 26/Sep/20 | ||
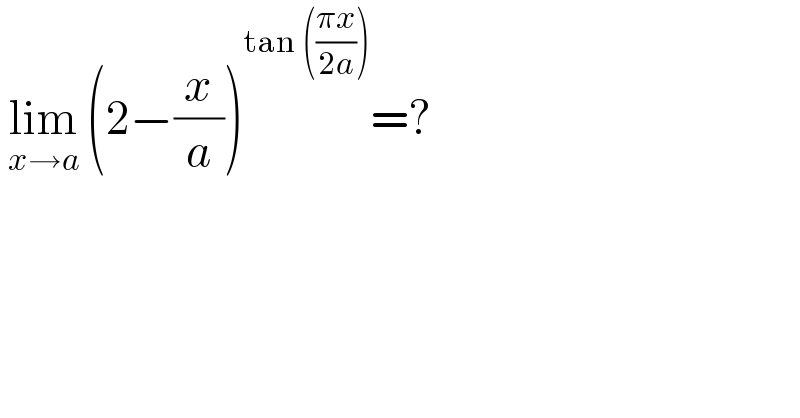 | ||
Answered by bemath last updated on 26/Sep/20 | ||
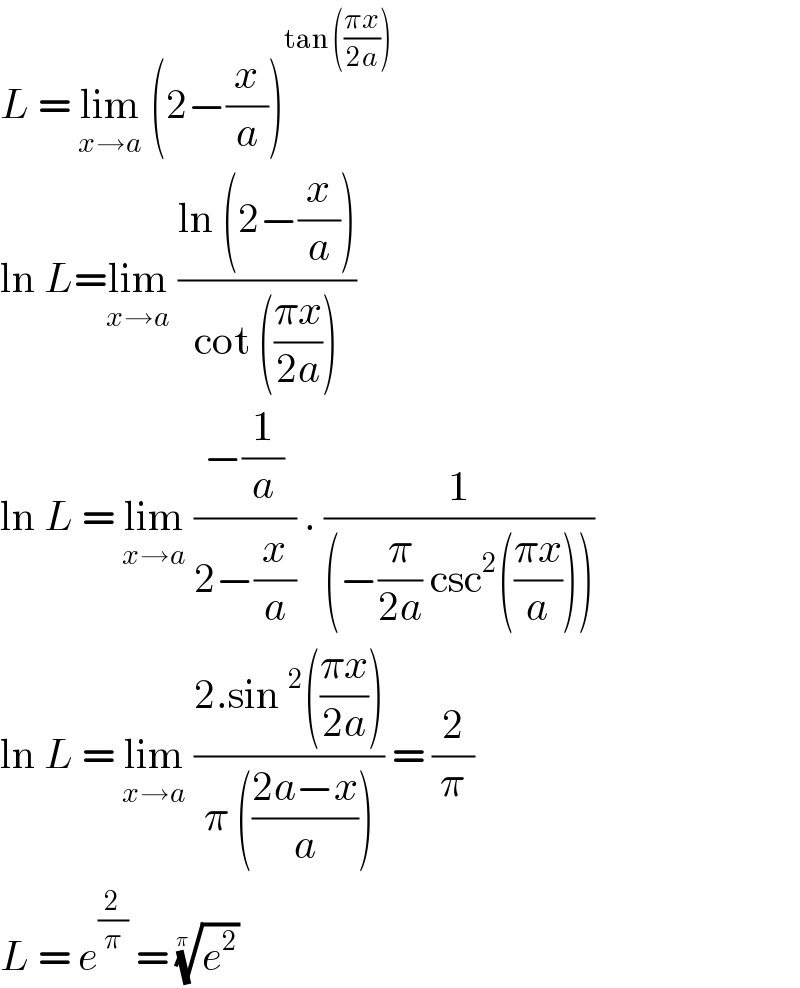 | ||
| ||
Answered by Dwaipayan Shikari last updated on 26/Sep/20 | ||
 | ||
| ||
Answered by mnjuly1970 last updated on 26/Sep/20 | ||
![solution: 1−(x/a) =t {_(t→0) ^(x→a) lim_(t→0) (1+t)^(tan[(π/2)(1−t)]) =lim_(t→0 ) (1+t)^(cot((π/2)t)) =_(t→0) ^( sin((π/2)t)∽(π/2)t) lim_(t→0) [((1+t)^(2/π) )^(1/t) ]^(cos((π/2)t)) =_(t→0) ^(cos((π/2)t)→1) =e^(2/π) ✓ m.n.july.1970](Q115553.png) | ||
| ||