Given that x,y∈R ∀ x^2 −y^2 =32, (x+y)^4 +(x−y)^4 =4352, Find the value of x^2 +y^2 .


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 115555 by ZiYangLee last updated on 26/Sep/20

$Given that x, y \in R \forall x^{2} - y^{2} = 32,$ ${(x + y)}^{4} + {(x - y)}^{4} = 4352,$ $Find the value of x^{2} + y^{2} .$
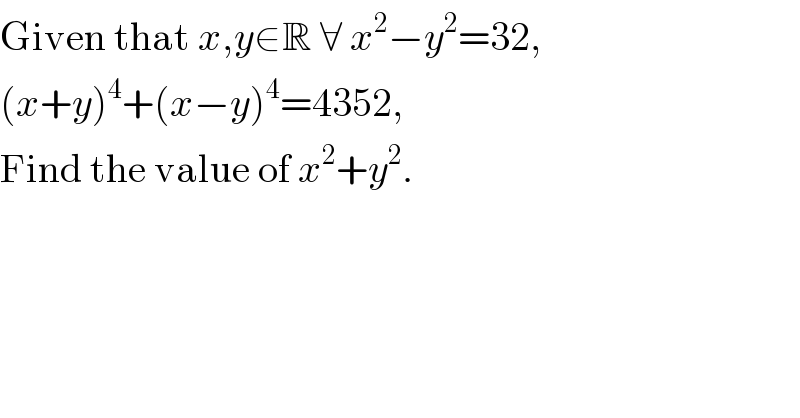
Commented by Rasheed.Sindhi last updated on 27/Sep/20

$A n O ther W ay$ $(B y c h a n g i n g i n t o$ $r e c i p r o c a l f o r m)$ ${(x + y)}^{4} + {(x - y)}^{4} = 4352$ $\frac{{(x + y)}^{4}}{{(x + y)}^{2} {(x - y)}^{2}} + \frac{{(x - y)}^{4}}{{(x + y)}^{2} {(x - y)}^{2}}$ $= \frac{4352}{{(x + y)}^{2} {(x - y)}^{2}}$ $\frac{{(x + y)}^{2}}{{(x - y)}^{2}} + \frac{{(x - y)}^{2}}{{(x + y)}^{2}} = \frac{4352}{{(x^{2} - y^{2})}^{2}}$ $\frac{{(x + y)}^{2}}{{(x - y)}^{2}} + \frac{{(x - y)}^{2}}{{(x + y)}^{2}} = \frac{4352}{{(32)}^{2}} = \frac{17}{4}$ $\frac{{(x + y)}^{2}}{{(x - y)}^{2}} = z$ $z + \frac{1}{z} = \frac{17}{4}$ $4 z^{2} - 17 z + 4 = 0$ $(z - 4) (4 z - 1) = 0$ $z = 4 \lor z = \frac{1}{4}$ $\frac{{(x + y)}^{2}}{{(x - y)}^{2}} = 4, \frac{1}{4}$ $\frac{{(x + y)}^{2}}{{(32 / (x + y))}^{2}} = 4, \frac{1}{4}$ ${(x + y)}^{4} = 4 {(32)}^{2}$ ${(x + y)}^{2} = \pm 64$ ${(x - y)}^{2} = {(32 / (x + y))}^{2} = 32^{2} / (\pm 64) = \pm 16$ $2 (x^{2} + y^{2}) = {(x + y)}^{2} + {(x - y)}^{2}$ $x^{2} + y^{2} = \frac{1}{2} (\pm 64 \pm 16) = \pm 40$
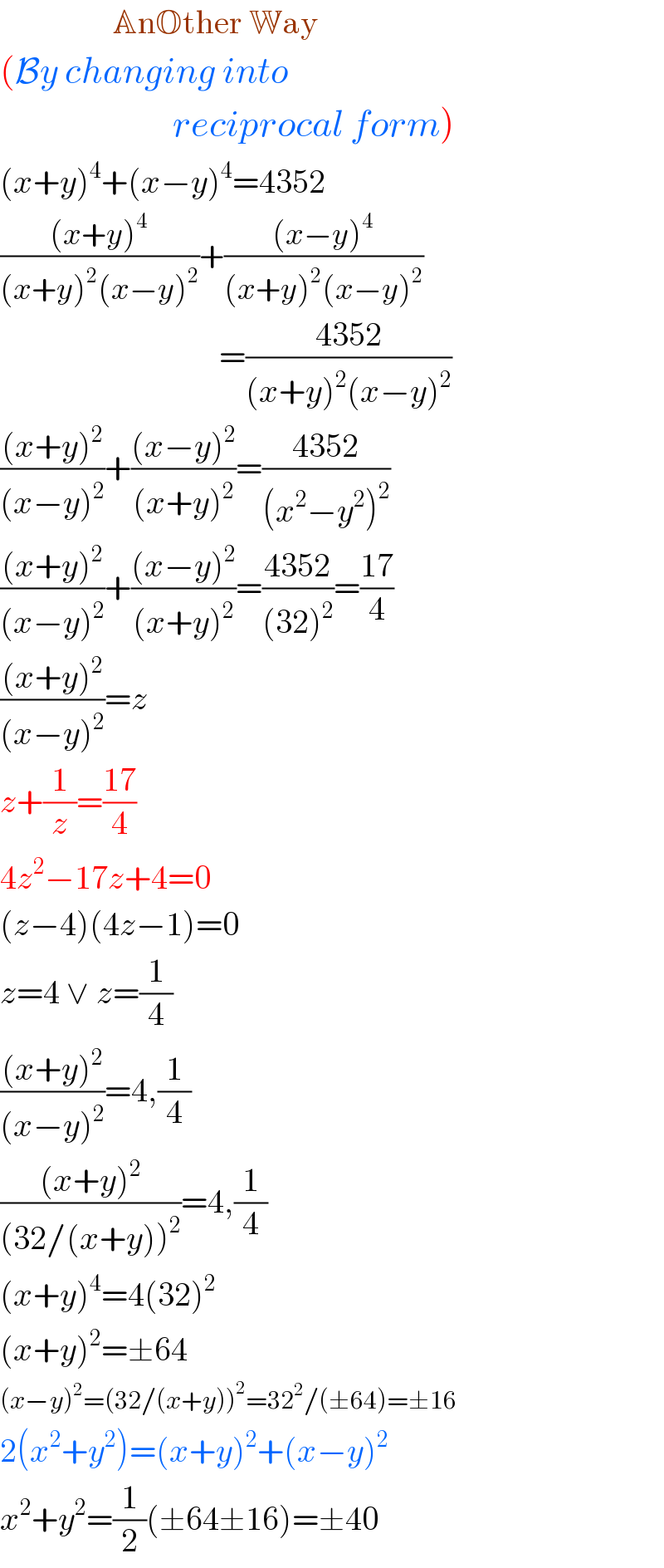
	Answered by mr W last updated on 26/Sep/20

	$u = x + y$ $v = x - y$ $x^{2} - y^{2} = (x + y) (x - y) = 32$ $\Rightarrow u v = 32$ $u^{4} + v^{4} = 4352$ $u^{4} + v^{4} + 2 u^{2} v^{2} = 4352 + 2 {(u v)}^{2}$ ${(u^{2} + v^{2})}^{2} = 4352 + 2 \times 32^{2} = 6400 = 80^{2}$ $\Rightarrow u^{2} + v^{2} = 80$ $u^{2} + v^{2} + 2 u v = 80 + 2 (u v)$ ${(u + v)}^{2} = 80 + 2 \times 32 = 144 = 12^{2}$ $\Rightarrow u + v = \pm 12$ $u^{2} + v^{2} - 2 u v = 80 - 2 (u v)$ ${(u - v)}^{2} = 80 - 2 \times 32 = 16 = 4^{2}$ $\Rightarrow u - v = \pm 4$ $x = \frac{u + v}{2} = \pm 6$ $y = \frac{u - v}{2} = \pm 2$ $\Rightarrow x^{2} + y^{2} = 36 + 4 = 40$
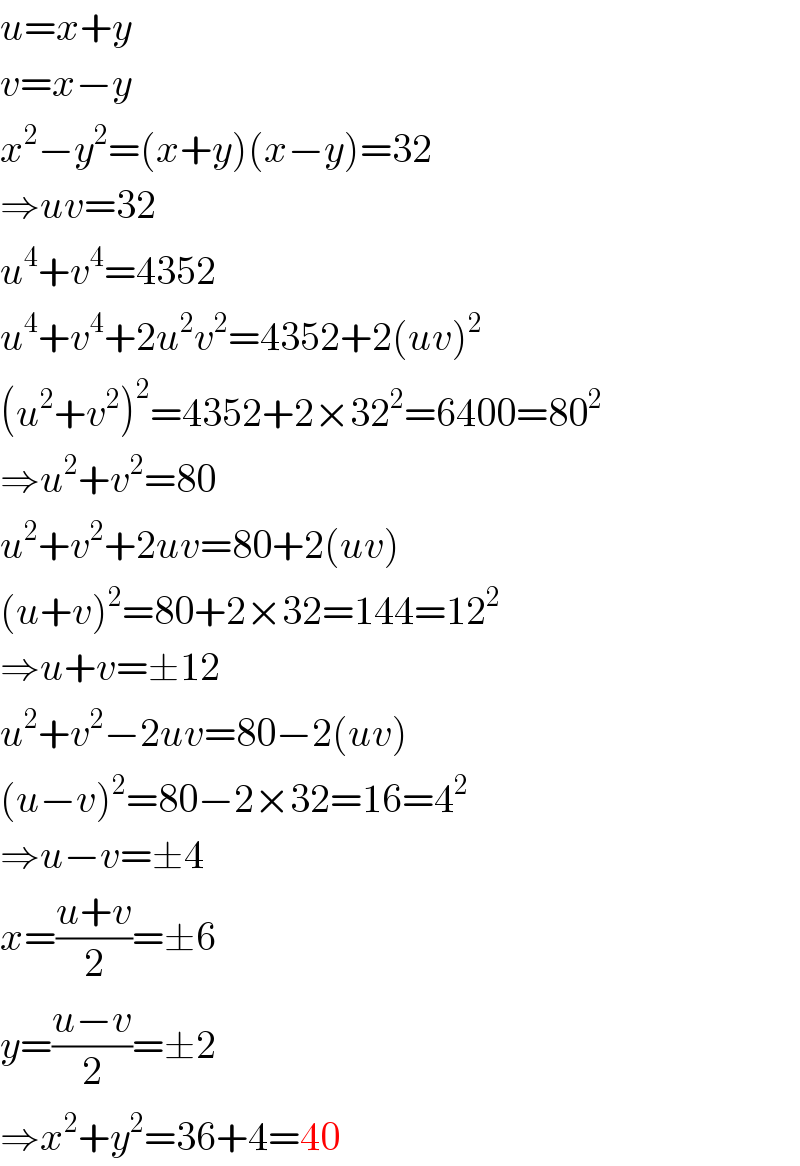
	Commented by ZiYangLee last updated on 26/Sep/20

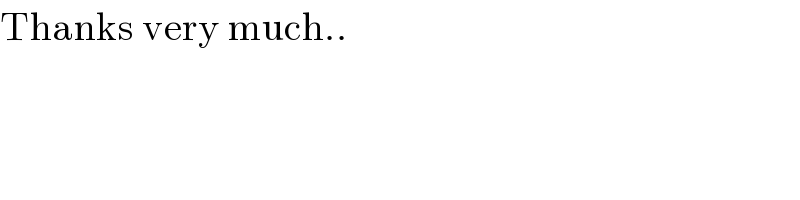
	$Thanks very much . .$
	Answered by ruwedkabeh last updated on 26/Sep/20

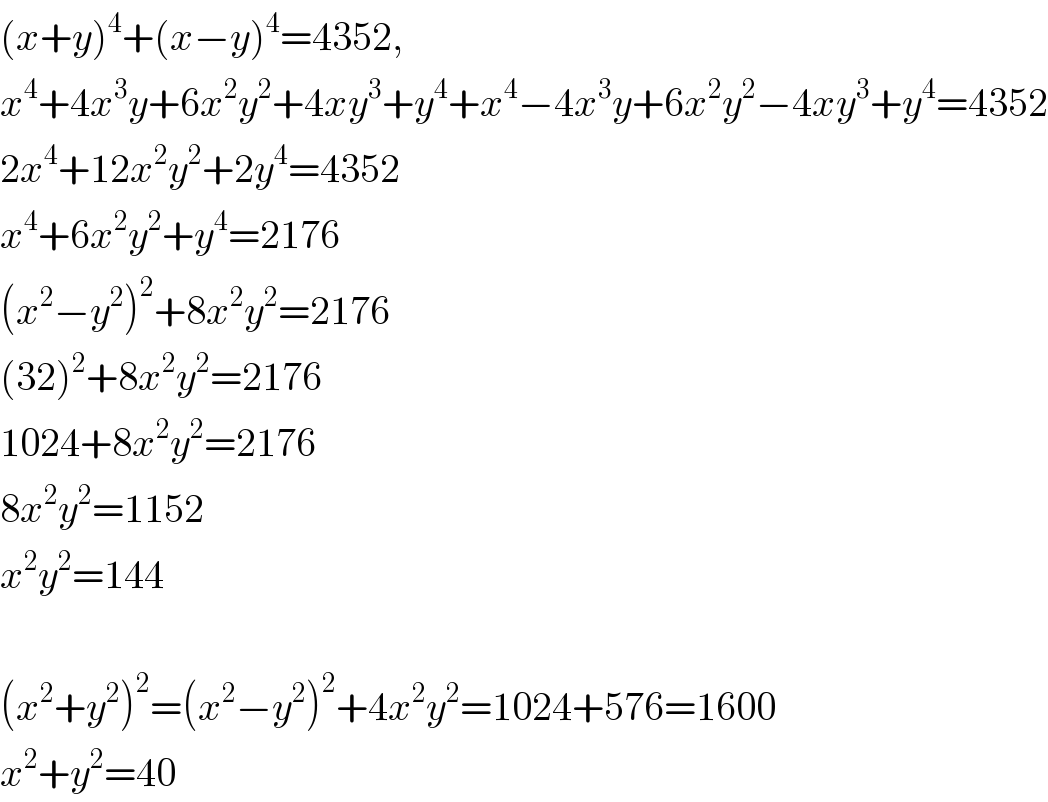
	${(x + y)}^{4} + {(x - y)}^{4} = 4352,$ $x^{4} + 4 x^{3} y + 6 x^{2} y^{2} + 4 {x y}^{3} + y^{4} + x^{4} - 4 x^{3} y + 6 x^{2} y^{2} - 4 {x y}^{3} + y^{4} = 4352$ $2 x^{4} + 12 x^{2} y^{2} + 2 y^{4} = 4352$ $x^{4} + 6 x^{2} y^{2} + y^{4} = 2176$ ${(x^{2} - y^{2})}^{2} + 8 x^{2} y^{2} = 2176$ ${(32)}^{2} + 8 x^{2} y^{2} = 2176$ $1024 + 8 x^{2} y^{2} = 2176$ $8 x^{2} y^{2} = 1152$ $x^{2} y^{2} = 144$ ${(x^{2} + y^{2})}^{2} = {(x^{2} - y^{2})}^{2} + 4 x^{2} y^{2} = 1024 + 576 = 1600$ $x^{2} + y^{2} = 40$
	Commented by ZiYangLee last updated on 26/Sep/20

	$Thank you!$
	Answered by Olaf last updated on 26/Sep/20

	${(x + y)}^{4} + {(x - y)}^{4} =$ ${[{(x + y)}^{2} + {(x - y)}^{2}]}^{2} - 2 {(x + y)}^{2} {(x - y)}^{2} =$ ${(2 x^{2} + 2 y^{2})}^{2} - 2 {(x^{2} - y^{2})}^{2} =$ $4 {(x^{2} + y^{2})}^{2} - 2 \times 32^{2} = 4352$ ${(x^{2} + y^{2})}^{2} = \frac{4352 + 2048}{4} = \frac{6400}{4} = 1600$ $x^{2} + y^{2} = 40$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum