Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 115558 by mnjuly1970 last updated on 26/Sep/20

$. . . a d v a n c e d c a l c u l u s . . .$ $e v a l u a t e ::$ $\int_{0}^{\infty} l n (1 + {a x}^{2}) l n (1 + \frac{b}{x^{2}}) d x$ $m . n . j u l y$
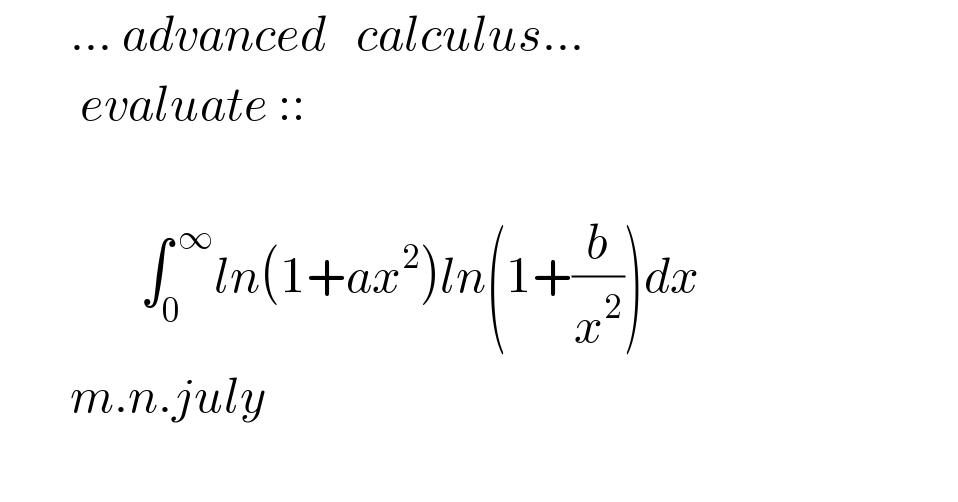
Commented by sachin1221 last updated on 26/Sep/20

$s h o w t h a t {l i m}_{n \to \infty} \frac{1}{n} [\frac{{c o s}^{2 p} π}{2 n} + \frac{{c o s}^{2 p} 2 π}{2 n} + \frac{{c o s}^{2 p} 3 π}{2 n} + . . . . . \frac{{c o s}^{2 p} π}{2}] = \underset{r = 1}{\prod^{p}} \frac{p + r}{4 r}$
Commented by TANMAY PANACEA last updated on 26/Sep/20

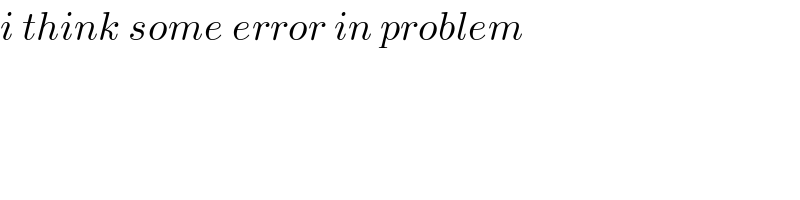
$i t h i n k s o m e e r r o r i n p r o b l e m$
	Answered by Olaf last updated on 26/Sep/20

	$I = \int_{0}^{\infty} \ln (1 + {a x}^{2}) \ln (1 + \frac{b}{x^{2}}) d x$ $a > 0, b > 0$ $I = \frac{π}{\sqrt{a}} (- 2 \sqrt{a b} + (\sqrt{a b} + 1) [\ln (1 - a b) + 2 \arctan \sqrt{ab}])$ $(Wolfram)$ $I will try to find the demonstration$ $but it may take time!$
	Commented by mnjuly1970 last updated on 26/Sep/20

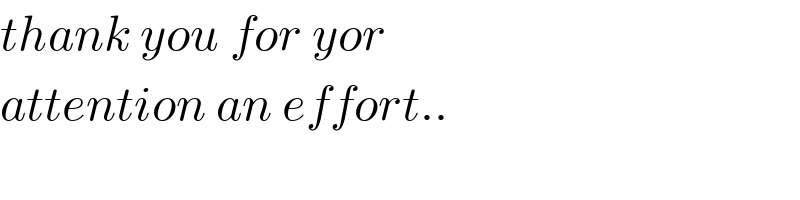
	$t h a n k y o u f o r y o r$ $a t t e n t i o n a n e f f o r t . .$
	Answered by maths mind last updated on 27/Sep/20
	$∫ln(1+ax^2 )dx=xln(1+ax^2 )−∫((2ax^2 )/(1+ax^2 ))dx =xln(1+ax^2 )−∫((2ax^2 +2−2)/(1+ax^2 ))dx =xln(1+ax^2 )−2x+(2/( (√a)))∫(((√a)dx)/(1+((√a)x)^2 )) =xln(1+ax^2 )−2x+(2/( (√a)))arctan(x(√a)) ∫_0 ^∞ ln(1+ax^2 )ln(1+(b/x^2 ))dx=G(a,b)∫ =[(xln(1+ax^2 )−2x+(2/( (√a)))arctan(x(√a))]ln(1+(b/x^2 ))]_0 ^∞ −∫_0 ^∞ (xln(1+ax^2 )−2x+(2/( (√a)))arctan(x(√a)))((−2b)/(x(x^2 +b)))dx =2b{∫_0 ^∞ ((ln(1+ax^2 ))/((x^2 +b)))dx−∫_0 ^∞ (2/(x^2 +b))+(2/( (√a)))∫_0 ^∞ ((arcran(x(√a)))/(x(x^2 +b)))dx ∫_0 ^∞ (2/(x^2 +b))dx=(2/( (√b)))∫(1/( (√b))).(dx/(1+((x/( (√b))))^2 ))=(2/( (√b))).(π/2)=(π/( (√b))) ∫_0 ^∞ ((ln(1+ax^2 ))/((x^2 +b)))=f(a)⇒f′(a)=∫_0 ^∞ (x^2 /((1+ax^2 )(x^2 +b))) a,b>0 =∫_0 ^∞ ((b(1+ax^2 )−(b+x^2 ))/((ba−1)(1+ax^2 )(x^2 +b)))dx=(b/(ba−1))∫_0 ^∞ (dx/(b+x^2 ))−(1/(ba−1))∫_0 ^∞ (dx/(1+ax^2 )) =((√b)/( (ba−1)))(π/2)−(1/( (√a)(ba−1)))(π/2) f(a)=(π/(2(√b)))ln(ba−1)+(π/( (√b)))th^− ((√(ab))) ∫_0 ^∞ ((arctan(x(√a)))/(x(b+x^2 )))dx=s(a,b) let x=y(√(b )) s=∫_0 ^∞ ((arctan(y(√(ab))))/(b(1+y^2 )y)) ∫_0 ^∞ ((arcran(st))/(t(1+t^2 )))dt=f(s),f′(s)=∫_0 ^∞ (dt/((1+s^2 t^2 )(1+t^2 ))) .=(1/(1−s^2 ))∫_0 ^∞ ((1/(1+t^2 ))−(s^2 /(1+s^2 t^2 )))dt =(π/(2(1−s^2 )))−(s/(1−s^2 )).(π/2) f(s)=∫_0 ^s ((π/(2(1−s^2 ))−(π/2).(s/(1−s^2 )))ds=(π/2)th^− (s)+(π/2)ln((√(1−s^2 ))) ⇒∫_0 ^∞ ((arctan(x(√a)))/(x(x^2 +b)))=(1/b)((π/2)th^− ((√(ab)))+(π/2)ln((√(∣1−ab∣)))) ∫_0 ^∞ ln(1+ax^2 )ln(1+(b/x^2 ))=2b((π/(2(√b)))ln(∣ba−1∣)+(π/( (√b)))th^− ((√(ab)))) −2b.(π/( (√b)))+2b.(2/( (√a)))((1/b)((π/2)th^− ((√(ab)))+(π/4)ln(∣ba−1∣)) =π((√b)+(1/( (√a))))ln∣ba−1∣+π(2(√b)+(2/( (√a))))th^− ((√(ab)))−2π(√b) =((π(−2(√(ab))+((√(ab))+1)ln∣ab−1∣+(2(√(ab))+2)th^− ((√(ab)))))/( (√a)))$
	$\int l n (1 + {a x}^{2}) d x = x l n (1 + {a x}^{2}) - \int \frac{2 {a x}^{2}}{1 + {a x}^{2}} d x$ $= x l n (1 + {a x}^{2}) - \int \frac{2 {a x}^{2} + 2 - 2}{1 + {a x}^{2}} d x$ $= x l n (1 + {a x}^{2}) - 2 x + \frac{2}{\sqrt{a}} \int \frac{\sqrt{a} d x}{1 + {(\sqrt{a} x)}^{2}}$ $= x l n (1 + {a x}^{2}) - 2 x + \frac{2}{\sqrt{a}} a r c t a n (x \sqrt{a})$ $\int_{0}^{\infty} l n (1 + {a x}^{2}) l n (1 + \frac{b}{x^{2}}) d x = G (a, b) \int$ $= {[(x l n (1 + {a x}^{2}) - 2 x + \frac{2}{\sqrt{a}} a r c t a n (x \sqrt{a})] l n (1 + \frac{b}{x^{2}})]}_{0}^{\infty}$ $- \int_{0}^{\infty} (x l n (1 + {a x}^{2}) - 2 x + \frac{2}{\sqrt{a}} a r c t a n (x \sqrt{a})) \frac{- 2 b}{x (x^{2} + b)} d x$ $= 2 b {\int_{0}^{\infty} \frac{l n (1 + {a x}^{2})}{(x^{2} + b)} d x - \int_{0}^{\infty} \frac{2}{x^{2} + b} + \frac{2}{\sqrt{a}} \int_{0}^{\infty} \frac{a r c r a n (x \sqrt{a})}{x (x^{2} + b)} d x$ $\int_{0}^{\infty} \frac{2}{x^{2} + b} d x = \frac{2}{\sqrt{b}} \int \frac{1}{\sqrt{b}} . \frac{d x}{1 + {(\frac{x}{\sqrt{b}})}^{2}} = \frac{2}{\sqrt{b}} . \frac{π}{2} = \frac{π}{\sqrt{b}}$ $\int_{0}^{\infty} \frac{l n (1 + {a x}^{2})}{(x^{2} + b)} = f (a) \Rightarrow f^{'} (a) = \int_{0}^{\infty} \frac{x^{2}}{(1 + {a x}^{2}) (x^{2} + b)} a, b > 0$ $= \int_{0}^{\infty} \frac{b (1 + {a x}^{2}) - (b + x^{2})}{(b a - 1) (1 + {a x}^{2}) (x^{2} + b)} d x = \frac{b}{b a - 1} \int_{0}^{\infty} \frac{d x}{b + x^{2}} - \frac{1}{b a - 1} \int_{0}^{\infty} \frac{d x}{1 + {a x}^{2}}$ $= \frac{\sqrt{b}}{(b a - 1)} \frac{π}{2} - \frac{1}{\sqrt{a} (b a - 1)} \frac{π}{2}$ $f (a) = \frac{π}{2 \sqrt{b}} l n (b a - 1) + \frac{π}{\sqrt{b}} {t h}^{-} (\sqrt{a b})$ $\int_{0}^{\infty} \frac{a r c t a n (x \sqrt{a})}{x (b + x^{2})} d x = s (a, b) l e t x = y \sqrt{b}$ $s = \int_{0}^{\infty} \frac{a r c t a n (y \sqrt{a b})}{b (1 + y^{2}) y}$ $\int_{0}^{\infty} \frac{a r c r a n (s t)}{t (1 + t^{2})} d t = f (s), f^{'} (s) = \int_{0}^{\infty} \frac{d t}{(1 + s^{2} t^{2}) (1 + t^{2})}$ $. = \frac{1}{1 - s^{2}} \int_{0}^{\infty} (\frac{1}{1 + t^{2}} - \frac{s^{2}}{1 + s^{2} t^{2}}) d t$ $= \frac{π}{2 (1 - s^{2})} - \frac{s}{1 - s^{2}} . \frac{π}{2}$ $f (s) = \int_{0}^{s} (\frac{π}{2 (1 - s^{2}} - \frac{π}{2} . \frac{s}{1 - s^{2}}) d s = \frac{π}{2} {t h}^{-} (s) + \frac{π}{2} l n (\sqrt{1 - s^{2})}$ $\Rightarrow \int_{0}^{\infty} \frac{a r c t a n (x \sqrt{a})}{x (x^{2} + b)} = \frac{1}{b} (\frac{π}{2} {t h}^{-} (\sqrt{a b}) + \frac{π}{2} l n (\sqrt{∣ 1 - a b ∣}))$ $\int_{0}^{\infty} l n (1 + {a x}^{2}) l n (1 + \frac{b}{x^{2}}) = 2 b (\frac{π}{2 \sqrt{b}} l n (∣ b a - 1 ∣) + \frac{π}{\sqrt{b}} {t h}^{-} (\sqrt{a b}))$ $- 2 b . \frac{π}{\sqrt{b}} + 2 b . \frac{2}{\sqrt{a}} (\frac{1}{b} (\frac{π}{2} {t h}^{-} (\sqrt{a b}) + \frac{π}{4} l n (∣ b a - 1 ∣))$ $= π (\sqrt{b} + \frac{1}{\sqrt{a}}) l n ∣ b a - 1 ∣ + π (2 \sqrt{b} + \frac{2}{\sqrt{a}}) {t h}^{-} (\sqrt{a b}) - 2 π \sqrt{b}$ $= \frac{π (- 2 \sqrt{a b} + (\sqrt{a b} + 1) l n ∣ a b - 1 ∣ + (2 \sqrt{a b} + 2) {t h}^{-} (\sqrt{a b}))}{\sqrt{a}}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum