Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 115594 by MJS_new last updated on 26/Sep/20

$$\mathrm{old}\mathrm{question},\mathrm{I}{\mathrm{couldn}}^{\prime }\mathrm{t}\mathrm{find}\mathrm{it}:$$$$\int \sqrt{x-\sqrt{x}}dx=?$$

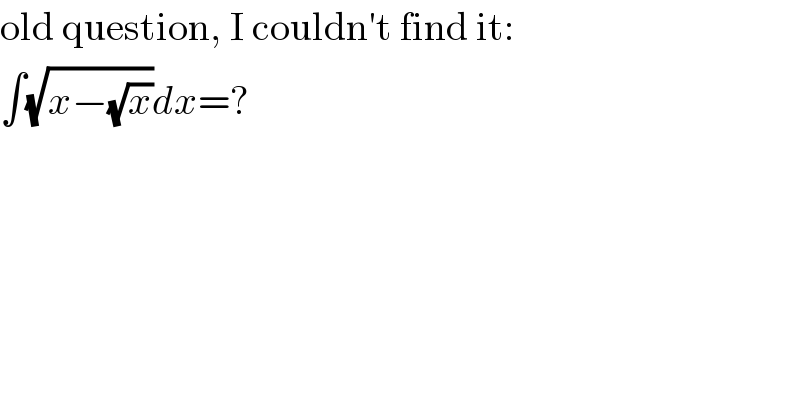
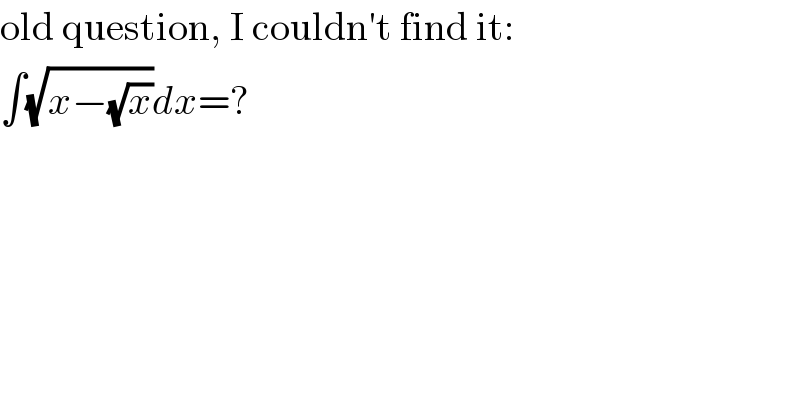Answered by MJS_new last updated on 26/Sep/20

$$\int \sqrt{x-\sqrt{x}}dx=$$$$[t=\sqrt{x}\to dx=2\sqrt{x}dt]$$$$=2\int t^{3/2}\sqrt{t-1}dt=$$$$[u=\sqrt{t-1}\to dt=2\sqrt{t-1}du]$$$$=4\int u^2{(u^2+1)}^{3/2}du=$$$$[v=u+\sqrt{u^2+1}\to du=\frac{\sqrt{u^2+1}}{u+\sqrt{u^2+1}}dv]$$$$=\frac{1}{16}\int \frac{v^{12}+2v^{10}-v^8-4v^6-v^4+2v^2+1}{v^7}dv=$$$$=\frac{v^6}{96}+\frac{v^4}{32}-\frac{v^2}{32}+\frac{1}{32v^2}-\frac{1}{32v^4}-\frac{1}{96v^6}-\frac{1}{4}\ln v=$$$$[v=u+\sqrt{u^2+1}\wedge u=\sqrt{t-1}\wedge t=\sqrt{x}]$$$$=\frac{1}{12}(8x-2\sqrt{x}-3)\sqrt{x-\sqrt{x}}-\frac{1}{4}\ln (\sqrt{\sqrt{x}-1}+\sqrt[4]{x})+C$$

Commented by Eric002 last updated on 27/Sep/20

$$niceworkithinkitsq115498$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com