.... advanced calculus... ... evaluate ... Ψ= ∫_(−∞) ^( +∞) ((x/(2+2^(−x) +2^x )))^2 dx =??? m.n.july 70


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 115761 by mnjuly1970 last updated on 28/Sep/20

$. . . . a d v a n c e d c a l c u l u s . . .$ $. . . e v a l u a t e . . .$ $Ψ = \int_{- \infty}^{+ \infty} {(\frac{x}{2 + 2^{- x} + 2^{x}})}^{2} d x = ? ? ?$ $m . n . j u l y 70$
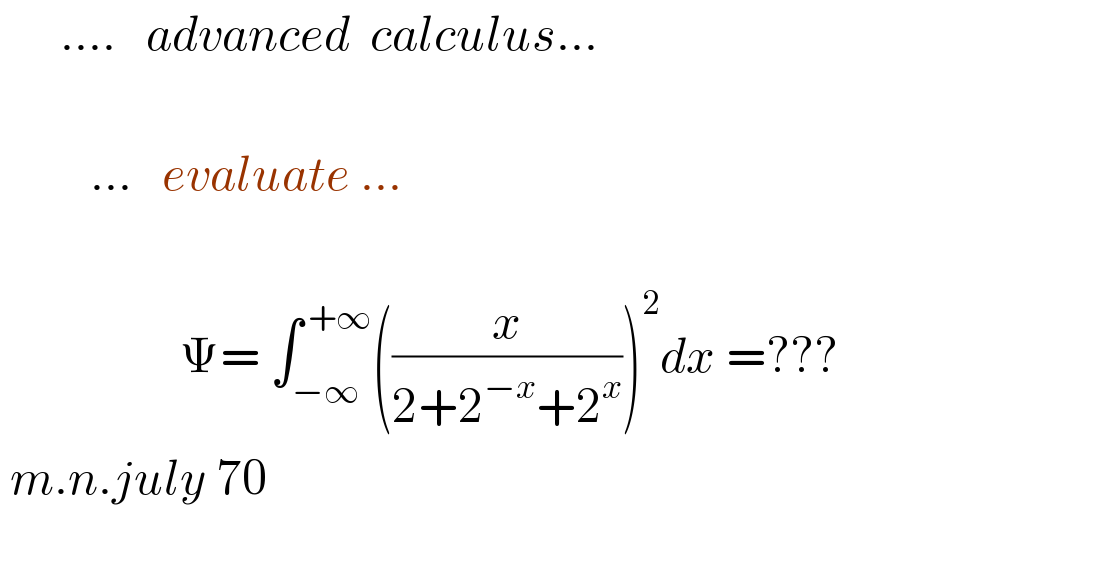
Commented by Olaf last updated on 28/Sep/20

$Ψ = 2 \int_{0}^{\infty} {(\frac{x}{2 + 2^{- x} + 2^{x}})}^{2} d x$ $u = 2^{x} = e^{x \ln 2}$ $d u = \ln 2 . e^{x \ln 2} d x \Rightarrow d x = \frac{d u}{u \ln 2}$ $Ψ = 2 \int_{1}^{\infty} {(\frac{\frac{\ln u}{\ln 2}}{2 + \frac{1}{u} + u})}^{2} \frac{d u}{u \ln 2}$ $Ψ = \frac{2}{\ln^{3} 2} \int_{1}^{\infty} u {(\frac{\ln u}{u^{2} + 2 u + 1})}^{2} d u$ $Ψ = \frac{2}{\ln^{3} 2} \int_{1}^{\infty} u \frac{\ln^{2} u}{{(u + 1)}^{4}} d u$ $\frac{u}{{(u + 1)}^{4}} = \frac{1}{{(u + 1)}^{3}} - \frac{1}{{(u + 1)}^{4}}$ $Ψ = \frac{2}{\ln^{3} 2} {[(- \frac{1}{2 {(u + 1)}^{2}} + \frac{1}{3 {(u + 1)}^{3}}) \ln^{2} u]}_{1}^{\infty}$ $- \frac{2}{\ln^{3} 2} \int_{1}^{\infty} (- \frac{1}{2 {(u + 1)}^{2}} + \frac{1}{3 {(u + 1)}^{3}}) 2 \frac{\ln u}{u}$ $Ψ = \frac{2}{\ln^{3} 2} \int_{1}^{\infty} \frac{\ln u}{u {(u + 1)}^{2}} d u - \frac{4}{{3 \ln}^{3} 2} \int_{1}^{\infty} \frac{\ln u}{u {(u + 1)}^{3}} d u$ $I = \int_{1}^{\infty} \frac{\ln u}{u {(u + 1)}^{2}} d u$ $J = \int_{1}^{\infty} \frac{\ln u}{u {(u + 1)}^{3}} d u$ $\frac{1}{u {(u + 1)}^{2}} = \frac{1}{u} - \frac{1}{1 + u} - \frac{1}{{(1 + u)}^{2}}$ $\frac{1}{u {(u + 1)}^{3}} = \frac{1}{u} - \frac{1}{1 + u} - \frac{1}{{(1 + u)}^{2}} - \frac{1}{{(1 + u)}^{3}}$ $Ψ = \frac{2}{\ln^{3} 2} I - \frac{4}{{3 \ln}^{3} 2} J$ $Ψ = \frac{2}{{3 \ln}^{3} 2} [\int_{1}^{\infty} \frac{\ln u}{u} d u - \int_{1}^{\infty} \frac{\ln u}{1 + u} d u - \int_{1}^{\infty} \frac{\ln u}{{(1 + u)}^{2}} d u] - \frac{4}{{3 \ln}^{3} 2} \int_{1}^{\infty} \frac{\ln u}{{(1 + u)}^{3}} d u$ $A_{0} = \int_{1}^{\infty} \frac{\ln u}{u} d u = \infty . . . ?$ $. . . {it}^{'} s probably false . I tried .$
	Answered by MJS_new last updated on 28/Sep/20

	$Ψ = 2 \underset{0}{\int^{\infty}} \frac{2^{2 x} x^{2}}{{(2^{x} + 1)}^{4}} d x$ $solving the integral \int \frac{2^{2 x} x^{2}}{{(2^{x} + 1)}^{4}} d x is easy :$ $(1) substitution t = 2^{x} + 1 and (2) solving$ $by parts; leading to$ $(1) \frac{1}{\ln^{3} 2} \int \frac{t - 1}{t^{4}} \ln^{2} (t - 1) d t$ $(2) \Rightarrow$ $\frac{1}{\ln^{3} 2} (\frac{1}{3 t} - \frac{1}{3} {Li}_{2} (t - 1) + \frac{t - 1}{3 t^{2}} (1 + \frac{(t - 1) (t + 2)}{2 t} \ln (t - 1)) \ln (t - 1) - \frac{1}{3} \ln t \ln (t - 1))$ $but I cannot find an exact value for Ψ$
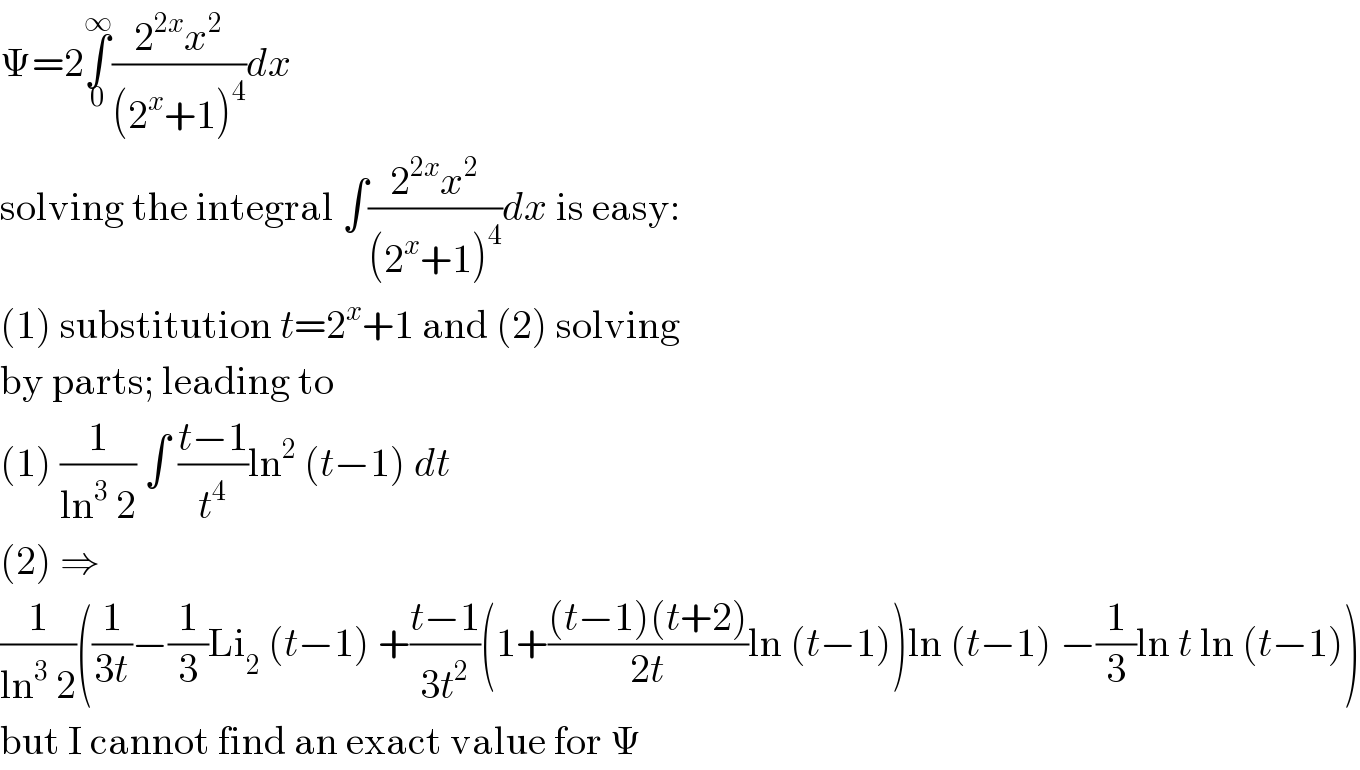
	Commented by mnjuly1970 last updated on 29/Sep/20

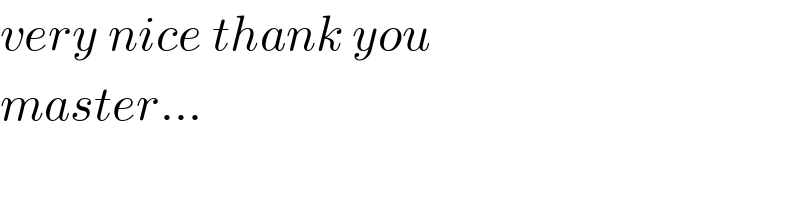
	$v e r y n i c e t h a n k y o u$ $m a s t e r . . .$
	Answered by maths mind last updated on 29/Sep/20
	$Ψ=2∫_0 ^∞ ((x^2 2^(2x) )/((1+2^(x+1) +2^(2x) )^2 ))dx =2∫_0 ^∞ ((2^(2x) x^2 )/((1+2^x )^4 )) let t=2^x ⇒x=((ln(t))/(ln(2))),dx=(dt/(tln(2))) =(2/(ln^3 (2)))∫_1 ^∞ ((tln^2 (t))/((1+t)^4 ))dt,t=(1/s) =(2/(ln^3 (2)))∫_0 ^1 ((sln^2 (s))/((1+s)^4 ))ds =(2/(ln^3 (2)))∫_0 ^1 (((ln^2 (s))/((1+s)^3 ))−((ln^2 (s))/((1+s)^4 )))ds=(2/(ln^3 (2)))[I−J] I=∫_0 ^1 ((ln^2 (s))/((1+s)^3 ))ds=lim_(x→0) [((−1)/(2(1+s)^2 ))ln^2 (s)]_x ^1 +∫_x ^1 ((ln(s))/(s(1+s)^2 ))ds =lim_(x→0) ((ln^2 (x))/(2(1+x)^2 ))+∫_x ^1 ((((1+s)^2 −s(1+s)−s))/(s(1+s)^2 )))ln(s)ds =lim_(x→0) ((ln^2 (x))/(2(1+x)^2 ))+∫_x ^1 ((ln(s))/s)ds−∫_0 ^1 ((ln(s))/(1+s))−∫_0 ^1 ((ln(s))/((s+1)^2 )) =lim_(x→0) ((1/(2(1+x)^2 ))−(1/2))ln^2 (x)−∫_0 ^1 Σ_(k≥0) (−1)^k s^k ln(s)ds −[[−((ln(s))/(1+s))]_x ^1 +∫_x ^1 (1/(s(s+1)))ds] =Σ_(k≥0) (−1)^k (1/((k+1)^2 ))−lim_(x→0) {((ln(x))/(1+x))+∫_x ^1 (1/s)ds−∫_x ^1 (1/(s+1))dx} I=(π^2 /(12))−lim_(x→0) {((ln(x))/(1+x))−ln(x)−ln(2)+ln(x+1)}=(π^2 /(12))+ln(2) J=∫_0 ^1 ((ln^2 (s))/((1+s)^4 ))ds =lim_(x→0) [−((ln^2 (s))/(3(1+s)^3 ))]_x ^1 +(2/3)∫_x ^1 ((ln(s))/(s(1+s)^3 ))ds] (1/(s(1+s)^3 ))=(((1+s)^3 −s(1+s)^2 −s(1+s)−s)/(s(1+s)^3 )) =lim_(x→0) ((ln^2 (x))/(3(1+x)^3 ))+(2/3)∫_x ^1 (((ln(s))/s)−((ln(s))/(1+s))−((ln(s))/((1+s)^2 ))−((ln(s))/((1+s)^3 ))) =lim_(x→0) (((ln^2 (x))/(3(1+x)^3 ))−((ln^2 (x))/3))_(=0) −(2/3)∫_0 ^1 ((ln(s))/(1+s))ds−(2/3)∫_0 ^1 ((ln(s))/((1+s)^2 ))−(2/3)∫_0 ^1 =−(2/3)Σ(((−1)^k )/((k+1)^2 ))−(2/3).−ln(2)−(2/3)lim_(x→0) {[((−ln(s))/(2(1+s)^2 ))]_x ^1 +∫_x ^1 (1/(2s(1+s)^2 ))} =(π^2 /(18))+((2ln(2))/3)−(2/3)lim_(x→0) [((ln(x))/(2(1+x)^2 ))+∫_x ^1 (((1+s)^2 −s(1+s)−s)/(2s(s+1)^2 ))ds =(π^2 /(18))+((2ln(2))/3)−(2/3)[((ln(x))/(2(1+x)^2 ))+∫_x ^1 (1/(2s))ds−(1/2)∫_0 ^1 (1/(1+s))−(1/2)∫_0 ^1 (1/((1+s)^2 ))] =(π^2 /(18))+((2ln(2))/3)−(2/3)lim_(x→0) {[((ln(x))/(2(1+x)^2 ))−((ln(x))/2)]_ −((ln(2))/2)+(1/2)((1/2)−1)]} =(π^2 /(18))+((2ln(2))/3)+((ln(2))/3)+(1/(16))=(π^2 /(18))+ln(2)+(1/6) Ψ=(2/(ln^3 (2)))[I−J]=(2/(ln^3 (2)))[(π^2 /(12))+ln(2)−((π^2 /(18))+ln(2)+(1/6))] =(2/(ln^3 (2)))[((π^2 −6)/(36))]=((π^2 −6)/(18ln^3 (2)))$
	$Ψ = 2 \int_{0}^{\infty} \frac{x^{2} 2^{2 x}}{{(1 + 2^{x + 1} + 2^{2 x})}^{2}} d x$ $= 2 \int_{0}^{\infty} \frac{2^{2 x} x^{2}}{{(1 + 2^{x})}^{4}}$ $l e t t = 2^{x} \Rightarrow x = \frac{l n (t)}{l n (2)}, d x = \frac{d t}{t l n (2)}$ $= \frac{2}{{l n}^{3} (2)} \int_{1}^{\infty} \frac{{t l n}^{2} (t)}{{(1 + t)}^{4}} d t, t = \frac{1}{s}$ $= \frac{2}{{l n}^{3} (2)} \int_{0}^{1} \frac{{s l n}^{2} (s)}{{(1 + s)}^{4}} d s$ $= \frac{2}{{l n}^{3} (2)} \int_{0}^{1} (\frac{{l n}^{2} (s)}{{(1 + s)}^{3}} - \frac{{l n}^{2} (s)}{{(1 + s)}^{4}}) d s = \frac{2}{{l n}^{3} (2)} [I - J]$ $I = \int_{0}^{1} \frac{{l n}^{2} (s)}{{(1 + s)}^{3}} d s = \lim_{x \to 0} {[\frac{- 1}{2 {(1 + s)}^{2}} {l n}^{2} (s)]}_{x}^{1} + \int_{x}^{1} \frac{l n (s)}{s {(1 + s)}^{2}} d s$ $= \lim_{x \to 0} \frac{{l n}^{2} (x)}{2 {(1 + x)}^{2}} + \int_{x}^{1} (\frac{{(1 + s)}^{2} - s (1 + s) - s)}{s {(1 + s)}^{2}}) l n (s) d s$ $= \lim_{x \to 0} \frac{{l n}^{2} (x)}{2 {(1 + x)}^{2}} + \int_{x}^{1} \frac{l n (s)}{s} d s - \int_{0}^{1} \frac{l n (s)}{1 + s} - \int_{0}^{1} \frac{l n (s)}{{(s + 1)}^{2}}$ $= \lim_{x \to 0} (\frac{1}{2 {(1 + x)}^{2}} - \frac{1}{2}) {l n}^{2} (x) - \int_{0}^{1} \sum_{k ⩾ 0} {(- 1)}^{k} s^{k} l n (s) d s$ $- [{[- \frac{l n (s)}{1 + s}]}_{x}^{1} + \int_{x}^{1} \frac{1}{s (s + 1)} d s]$ $= \sum_{k ⩾ 0} {(- 1)}^{k} \frac{1}{{(k + 1)}^{2}} - \lim_{x \to 0} {\frac{l n (x)}{1 + x} + \int_{x}^{1} \frac{1}{s} d s - \int_{x}^{1} \frac{1}{s + 1} d x}$ $I = \frac{π^{2}}{12} - \lim_{x \to 0} {\frac{l n (x)}{1 + x} - l n (x) - l n (2) + l n (x + 1)} = \frac{π^{2}}{12} + l n (2)$ $J = \int_{0}^{1} \frac{{l n}^{2} (s)}{{(1 + s)}^{4}} d s$ $= \lim_{x \to 0} {[- \frac{{l n}^{2} (s)}{3 {(1 + s)}^{3}}]}_{x}^{1} + \frac{2}{3} \int_{x}^{1} \frac{l n (s)}{s {(1 + s)}^{3}} d s]$ $\frac{1}{s {(1 + s)}^{3}} = \frac{{(1 + s)}^{3} - s {(1 + s)}^{2} - s (1 + s) - s}{s {(1 + s)}^{3}}$ $= \lim_{x \to 0} \frac{{l n}^{2} (x)}{3 {(1 + x)}^{3}} + \frac{2}{3} \int_{x}^{1} (\frac{l n (s)}{s} - \frac{l n (s)}{1 + s} - \frac{l n (s)}{{(1 + s)}^{2}} - \frac{l n (s)}{{(1 + s)}^{3}})$ $= \lim_{x \to 0} {(\frac{{l n}^{2} (x)}{3 {(1 + x)}^{3}} - \frac{{l n}^{2} (x)}{3})}_{= 0} - \frac{2}{3} \int_{0}^{1} \frac{l n (s)}{1 + s} d s - \frac{2}{3} \int_{0}^{1} \frac{l n (s)}{{(1 + s)}^{2}} - \frac{2}{3} \int_{0}^{1}$ $= - \frac{2}{3} Σ \frac{{(- 1)}^{k}}{{(k + 1)}^{2}} - \frac{2}{3} . - l n (2) - \frac{2}{3} \lim_{x \to 0} {{[\frac{- l n (s)}{2 {(1 + s)}^{2}}]}_{x}^{1} + \int_{x}^{1} \frac{1}{2 s {(1 + s)}^{2}}}$ $= \frac{π^{2}}{18} + \frac{2 l n (2)}{3} - \frac{2}{3} \lim_{x \to 0} [\frac{l n (x)}{2 {(1 + x)}^{2}} + \int_{x}^{1} \frac{{(1 + s)}^{2} - s (1 + s) - s}{2 s {(s + 1)}^{2}} d s$ $= \frac{π^{2}}{18} + \frac{2 l n (2)}{3} - \frac{2}{3} [\frac{l n (x)}{2 {(1 + x)}^{2}} + \int_{x}^{1} \frac{1}{2 s} d s - \frac{1}{2} \int_{0}^{1} \frac{1}{1 + s} - \frac{1}{2} \int_{0}^{1} \frac{1}{{(1 + s)}^{2}}]$ $= \frac{π^{2}}{18} + \frac{2 l n (2)}{3} - \frac{2}{3} \lim_{x \to 0} {{[\frac{l n (x)}{2 {(1 + x)}^{2}} - \frac{l n (x)}{2}]}_{} - \frac{l n (2)}{2} + \frac{1}{2} (\frac{1}{2} - 1)]}$ $= \frac{π^{2}}{18} + \frac{2 l n (2)}{3} + \frac{l n (2)}{3} + \frac{1}{16} = \frac{π^{2}}{18} + l n (2) + \frac{1}{6}$ $Ψ = \frac{2}{{l n}^{3} (2)} [I - J] = \frac{2}{{l n}^{3} (2)} [\frac{π^{2}}{12} + l n (2) - (\frac{π^{2}}{18} + l n (2) + \frac{1}{6})]$ $= \frac{2}{{l n}^{3} (2)} [\frac{π^{2} - 6}{36}] = \frac{π^{2} - 6}{18 {l n}^{3} (2)}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum