Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

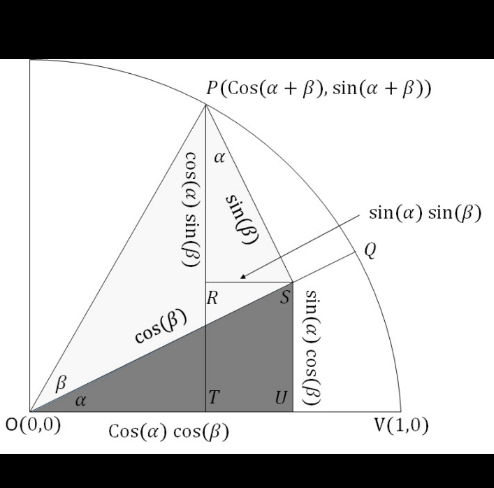
Question Number 115765 by aye48 last updated on 28/Sep/20

$$$$$$\mathrm{Show}\mathrm{that}\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta .$$

Commented by bemath last updated on 28/Sep/20

Commented by aye48 last updated on 28/Sep/20

$$\mathrm{Tk}\mathrm{yu}\mathrm{sir},\mathrm{explain}\mathrm{step}\mathrm{by}\mathrm{step}\mathrm{pl}.$$

Commented by Ar Brandon last updated on 28/Sep/20

$$\sin (\alpha +\beta )=\frac{\mathrm{PT}}{\mathrm{OP}}=\frac{\mathrm{RT}+\mathrm{PR}}{\mathrm{OP}}=\frac{\mathrm{SU}+\mathrm{PR}}{\mathrm{OP}}$$$$=\frac{\mathrm{SU}}{\mathrm{OP}}+\frac{\mathrm{PR}}{\mathrm{OP}}=\frac{\mathrm{SU}}{\mathrm{OS}}\times \frac{\mathrm{OS}}{\mathrm{OP}}+\frac{\mathrm{PR}}{\mathrm{PS}}\times \frac{\mathrm{PS}}{\mathrm{OP}}$$$$=\mathbf{sin}\mathit{\alpha }\mathbf{cos}\mathit{\beta }+\mathbf{cos}\mathit{\alpha }\mathbf{sin}\mathit{\beta }$$

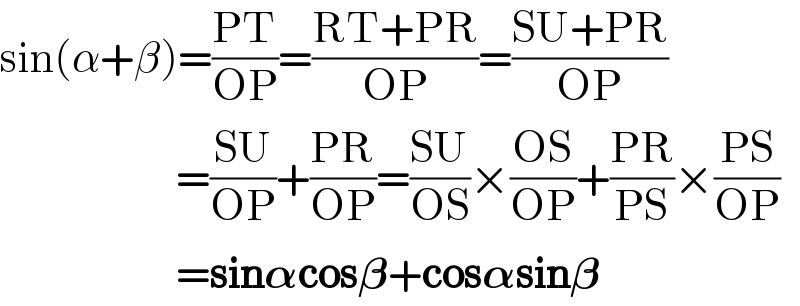
Answered by MJS_new last updated on 28/Sep/20

$$\mathrm{remember}$$$$\sin x=\frac{{\mathrm{e}}^{\mathrm{i}x}-{\mathrm{e}}^{-\mathrm{i}x}}{2\mathrm{i}}=-\frac{\mathrm{i}}{2}({\mathrm{e}}^{\mathrm{i}x}-\frac{1}{{\mathrm{e}}^{\mathrm{i}x}})$$$$\cos x=\frac{{\mathrm{e}}^{\mathrm{u}x}+{\mathrm{e}}^{-\mathrm{i}x}}{2}$$$$\Rightarrow$$$$\sin (\alpha +\beta )=-\frac{\mathrm{i}}{2}({\mathrm{e}}^{\mathrm{i}\alpha }{\mathrm{e}}^{\mathrm{i}\beta }-\frac{1}{{\mathrm{e}}^{\mathrm{i}\alpha }{\mathrm{e}}^{\mathrm{i}\beta }})=$$$$[\mathrm{let}{\mathrm{e}}^{\mathrm{i}\alpha }=p\wedge {\mathrm{e}}^{\mathrm{i}\beta }=q]$$$$=-\frac{\mathrm{i}}{2}(pq-\frac{1}{pq})=$$$$[\mathrm{now}\mathrm{the}\mathrm{trick}:]$$$$=-\frac{\mathrm{i}}{4}(2pq-\frac{2}{pq})=$$$$=-\frac{\mathrm{i}}{4}(2pq-\frac{2}{pq}+(\frac{p}{q}+\frac{q}{p})-(\frac{p}{q}+\frac{q}{p}))=$$$$=-\frac{\mathrm{i}}{4}((pq+\frac{p}{q}-\frac{q}{p}-\frac{1}{pq})+(pq-\frac{p}{q}+\frac{q}{p}-\frac{1}{pq}))=$$$$=-\frac{\mathrm{i}}{4}((p-\frac{1}{p})(q+\frac{1}{q})+(p+\frac{1}{p})(q-\frac{1}{q}))=$$$$=-\frac{\mathrm{i}(p-\frac{1}{p})}{2}\times \frac{q+\frac{1}{q}}{2}-\frac{p+\frac{1}{p}}{2}\times \frac{\mathrm{i}(q-\frac{1}{q})}{2}=$$$$=\frac{{\mathrm{e}}^{\mathrm{i}\alpha }-{\mathrm{e}}^{-\mathrm{i}\alpha }}{2\mathrm{i}}\times \frac{{\mathrm{e}}^{\mathrm{i}\beta }+{\mathrm{e}}^{-\mathrm{i}\beta }}{2}+\frac{{\mathrm{e}}^{\mathrm{i}\alpha }+{\mathrm{e}}^{-\mathrm{i}\alpha }}{2}\times \frac{{\mathrm{e}}^{\mathrm{i}\beta }-{\mathrm{e}}^{-\mathrm{i}\beta }}{2\mathrm{i}}=$$$$=\sin \alpha \cos \beta +\cos \alpha \sin \beta$$

Commented by Dwaipayan Shikari last updated on 28/Sep/20

$$\mathrm{Great}\mathrm{thinking}\mathrm{sir}!$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com