
Question and Answers Forum
Question Number 115777 by bemath last updated on 28/Sep/20
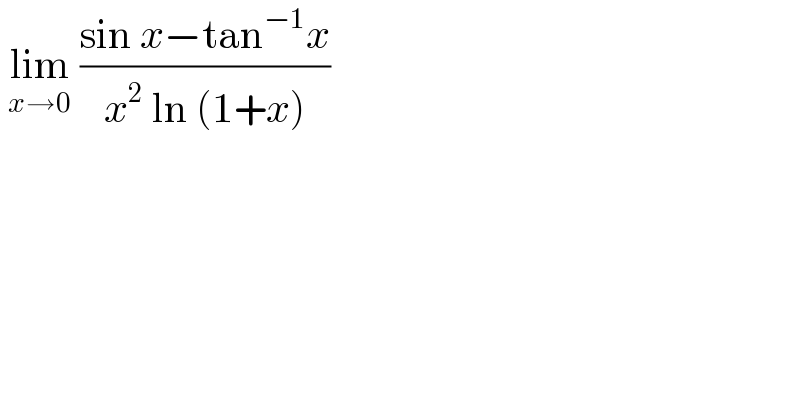
Answered by bobhans last updated on 28/Sep/20
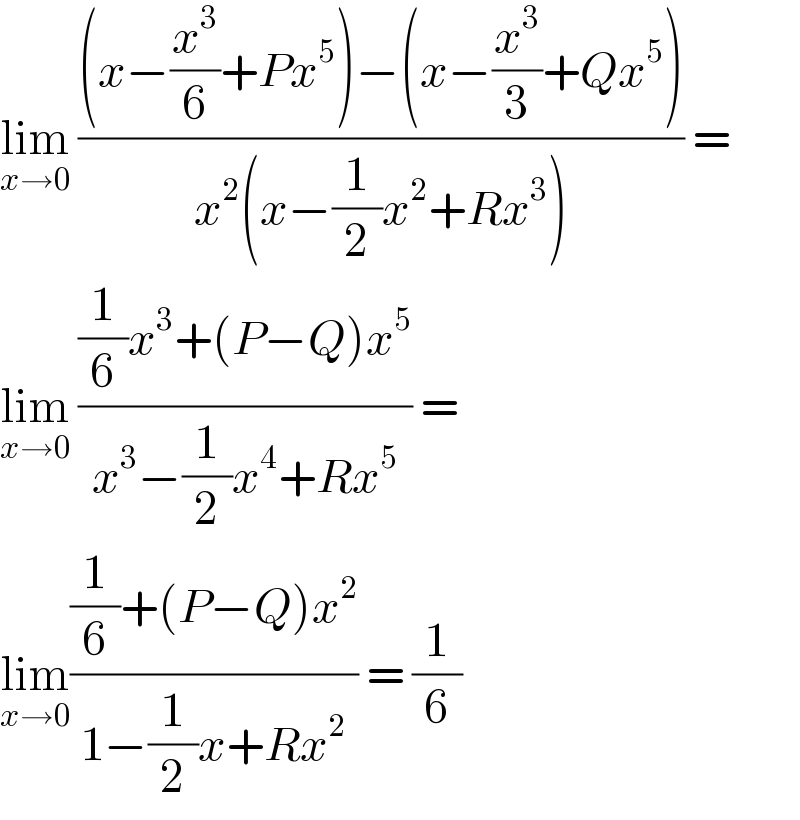
Answered by Olaf last updated on 28/Sep/20
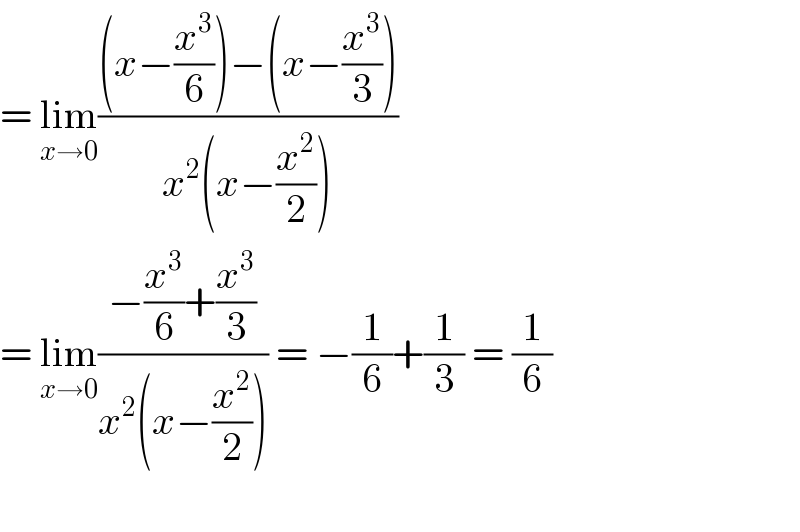
Answered by Dwaipayan Shikari last updated on 28/Sep/20
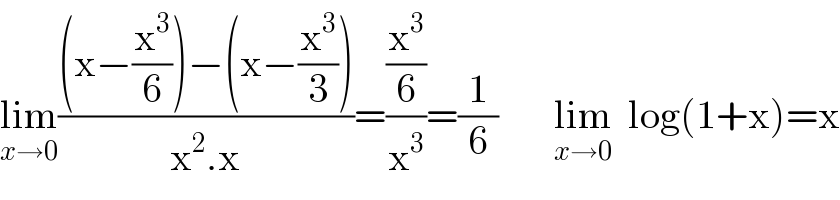
| ||
Question and Answers Forum | ||
Question Number 115777 by bemath last updated on 28/Sep/20 | ||
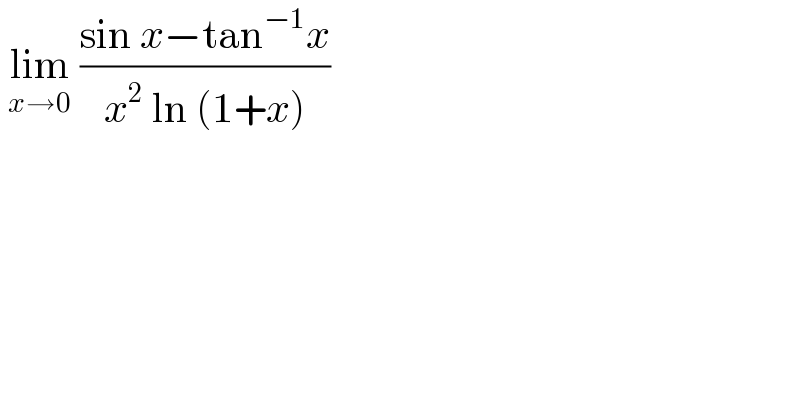 | ||
Answered by bobhans last updated on 28/Sep/20 | ||
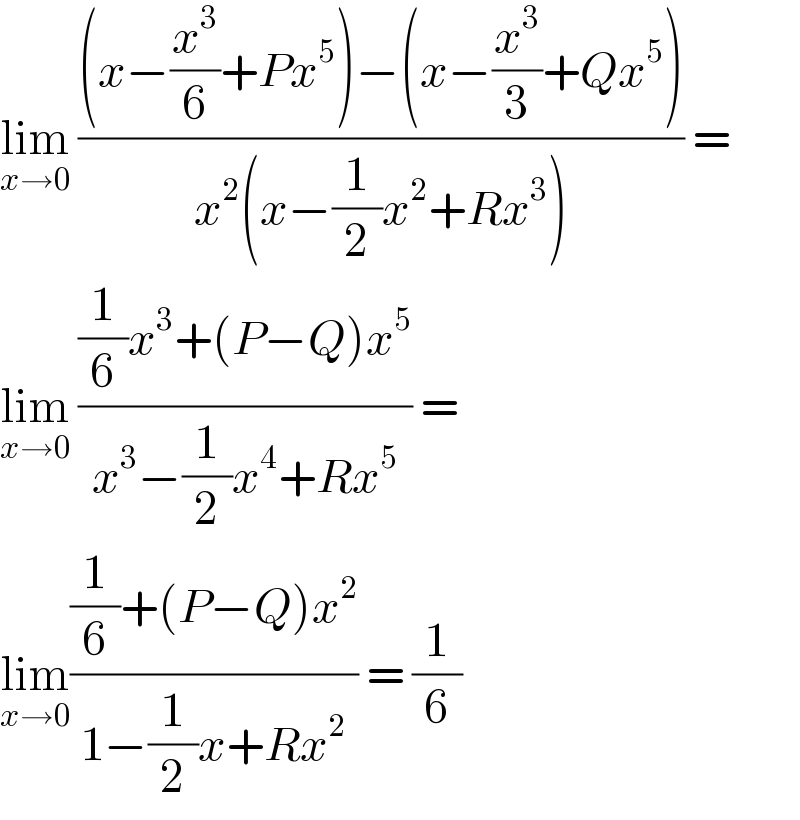 | ||
| ||
Answered by Olaf last updated on 28/Sep/20 | ||
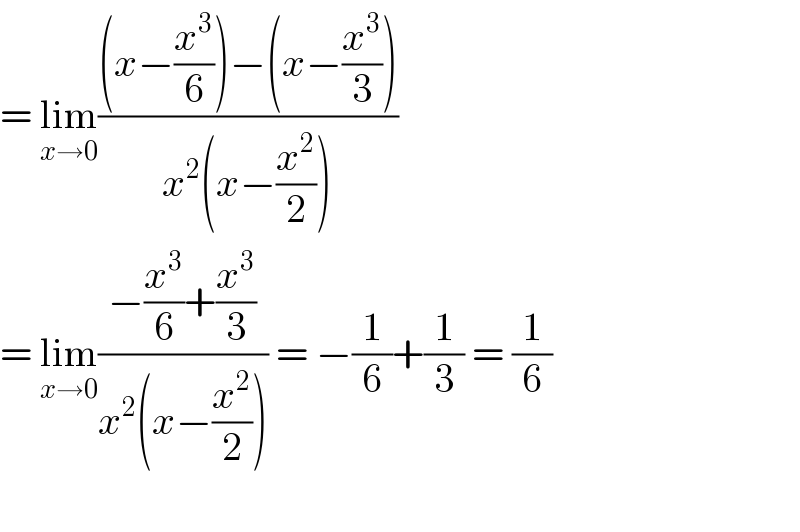 | ||
| ||
Answered by Dwaipayan Shikari last updated on 28/Sep/20 | ||
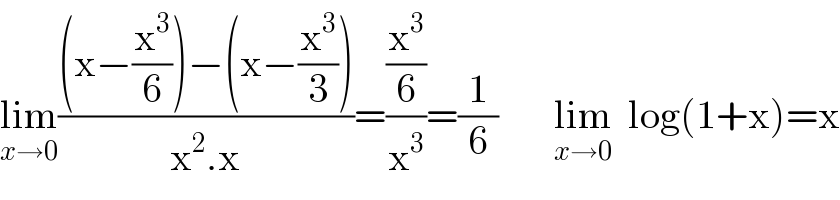 | ||
| ||