
Question and Answers Forum
Question Number 115908 by Eric002 last updated on 29/Sep/20
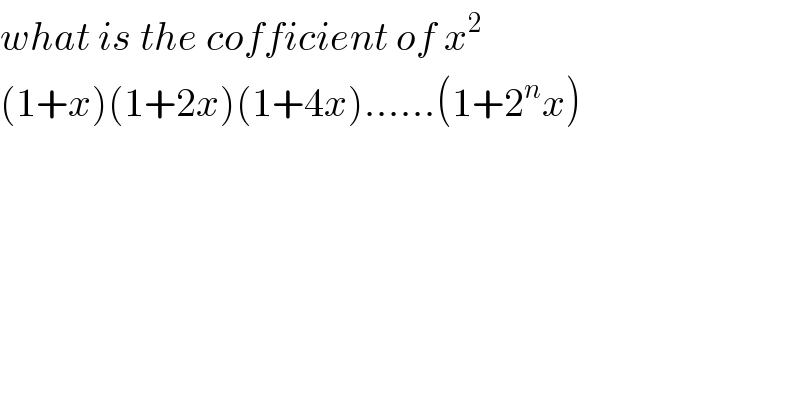
Commented by soumyasaha last updated on 29/Sep/20
![Coefficient = (1/2)[ (Σ_(r=0) ^n 2^r )^2 − Σ_(r=0) ^n (2^r )^2 ] = (1/2)[ (2^(n+1) −1)^2 − (1/3)(4^(n+1) −1)]](Q115937.png)
Commented by prakash jain last updated on 29/Sep/20

Answered by mr W last updated on 29/Sep/20
![(1/2)Σ_(k=0) ^n 2^k Σ_(i=0≠k) ^n 2^i =(1/2)Σ_(k=0) ^n 2^k (Σ_(i=0) ^n 2^i −2^k ) =(1/2)Σ_(k=0) ^n 2^k (((2^(n+1) −1)/(2−1))−2^k ) =(1/2)Σ_(k=0) ^n 2^k (2^(n+1) −1−2^k ) =(1/2)(2^(n+1) −1)Σ_(k=0) ^n 2^k −(1/2)Σ_(k=0) ^n 4^k =(1/2)(2^(n+1) −1)(2^(n+1) −1)−(1/2)×((4^(n+1) −1)/(4−1)) =(1/2)[2^(2(n+1)) −2×2^(n+1) +1]−((2^(2(n+1)) −1)/(2×3)) =((2(2^(2n+1) +1))/3)−2^(n+1) example n=2: =((2(2^5 +1))/3)−2^3 =14](Q115947.png)
| ||
Question and Answers Forum | ||
Question Number 115908 by Eric002 last updated on 29/Sep/20 | ||
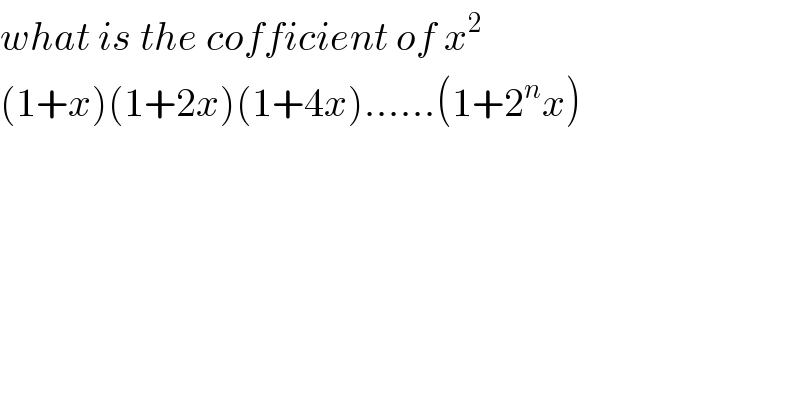 | ||
Commented by soumyasaha last updated on 29/Sep/20 | ||
![Coefficient = (1/2)[ (Σ_(r=0) ^n 2^r )^2 − Σ_(r=0) ^n (2^r )^2 ] = (1/2)[ (2^(n+1) −1)^2 − (1/3)(4^(n+1) −1)]](Q115937.png) | ||
Commented by prakash jain last updated on 29/Sep/20 | ||
 | ||
Answered by mr W last updated on 29/Sep/20 | ||
![(1/2)Σ_(k=0) ^n 2^k Σ_(i=0≠k) ^n 2^i =(1/2)Σ_(k=0) ^n 2^k (Σ_(i=0) ^n 2^i −2^k ) =(1/2)Σ_(k=0) ^n 2^k (((2^(n+1) −1)/(2−1))−2^k ) =(1/2)Σ_(k=0) ^n 2^k (2^(n+1) −1−2^k ) =(1/2)(2^(n+1) −1)Σ_(k=0) ^n 2^k −(1/2)Σ_(k=0) ^n 4^k =(1/2)(2^(n+1) −1)(2^(n+1) −1)−(1/2)×((4^(n+1) −1)/(4−1)) =(1/2)[2^(2(n+1)) −2×2^(n+1) +1]−((2^(2(n+1)) −1)/(2×3)) =((2(2^(2n+1) +1))/3)−2^(n+1) example n=2: =((2(2^5 +1))/3)−2^3 =14](Q115947.png) | ||
| ||