Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 115968 by Engr_Jidda last updated on 29/Sep/20

Answered by 1549442205PVT last updated on 30/Sep/20

Put u(x,y)=x^2 −1;v(x,y)=y^2 +1 The condition Cauchy−Rieman for the analytical is (∂u/∂x)=(∂v/∂y)(1),(∂u/∂y)=−(∂v/∂x)(2) We have (∂u/∂x)=2x,(∂u/∂y)=0,(∂v/∂x)=0,(∂v/∂y)=2y Henece,we need must have 2x=2y(second condition is satisfied ∀x,y)⇔y=x Thus,f(z) is analytical function on the line y=x and we have : f ′(z)=(∂u/∂x)+i(∂v/∂x)=(∂u/∂x)−i(∂u/∂y)=(∂v/∂y)−i(∂u/∂y)=(∂v/∂y)+i(∂v/∂x) =2x=2y

$$\mathrm{Put}\:\mathrm{u}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{1};\mathrm{v}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{y}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{The}\:\mathrm{condition}\:\mathrm{Cauchy}−\mathrm{Rieman}\:\mathrm{for} \\ $$$$\mathrm{the}\:\mathrm{analytical}\:\mathrm{is}\:\frac{\partial\mathrm{u}}{\partial\mathrm{x}}=\frac{\partial\mathrm{v}}{\partial\mathrm{y}}\left(\mathrm{1}\right),\frac{\partial\mathrm{u}}{\partial\mathrm{y}}=−\frac{\partial\mathrm{v}}{\partial\mathrm{x}}\left(\mathrm{2}\right) \\ $$$$\mathrm{We}\:\mathrm{have}\:\frac{\partial\mathrm{u}}{\partial\mathrm{x}}=\mathrm{2x},\frac{\partial\mathrm{u}}{\partial\mathrm{y}}=\mathrm{0},\frac{\partial\mathrm{v}}{\partial\mathrm{x}}=\mathrm{0},\frac{\partial\mathrm{v}}{\partial\mathrm{y}}=\mathrm{2y} \\ $$$$\mathrm{Henece},\mathrm{we}\:\mathrm{need}\:\mathrm{must}\:\mathrm{have} \\ $$$$\mathrm{2x}=\mathrm{2y}\left(\mathrm{second}\:\mathrm{condition}\:\mathrm{is}\:\mathrm{satisfied}\right. \\ $$$$\left.\forall\mathrm{x},\mathrm{y}\right)\Leftrightarrow\mathrm{y}=\mathrm{x} \\ $$$$\mathrm{Thus},\mathrm{f}\left(\mathrm{z}\right)\:\mathrm{is}\:\mathrm{analytical}\:\mathrm{function} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{x}\:\mathrm{and}\:\mathrm{we}\:\mathrm{have}\:: \\ $$$$\mathrm{f}\:'\left(\mathrm{z}\right)=\frac{\partial\mathrm{u}}{\partial\mathrm{x}}+\mathrm{i}\frac{\partial\mathrm{v}}{\partial\mathrm{x}}=\frac{\partial\mathrm{u}}{\partial\mathrm{x}}−\mathrm{i}\frac{\partial\mathrm{u}}{\partial\mathrm{y}}=\frac{\partial\mathrm{v}}{\partial\mathrm{y}}−\mathrm{i}\frac{\partial\mathrm{u}}{\partial\mathrm{y}}=\frac{\partial\mathrm{v}}{\partial\mathrm{y}}+\mathrm{i}\frac{\partial\mathrm{v}}{\partial\mathrm{x}} \\ $$$$=\mathrm{2x}=\mathrm{2y} \\ $$

Commented by Engr_Jidda last updated on 30/Sep/20

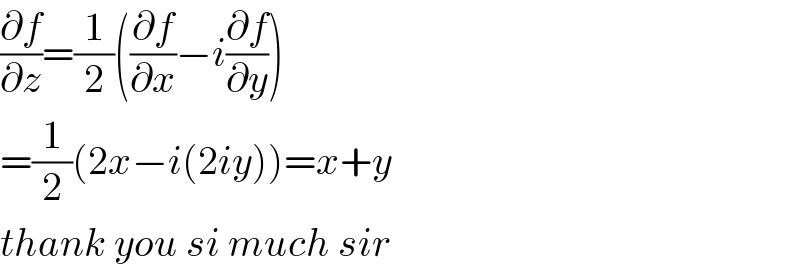
(∂f/∂z)=(1/2)((∂f/∂x)−i(∂f/∂y)) =(1/2)(2x−i(2iy))=x+y thank you si much sir

$$\frac{\partial{f}}{\partial{z}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\partial{f}}{\partial{x}}−{i}\frac{\partial{f}}{\partial{y}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}−{i}\left(\mathrm{2}{iy}\right)\right)={x}+{y} \\ $$$${thank}\:{you}\:{si}\:{much}\:{sir} \\ $$

Commented by Engr_Jidda last updated on 30/Sep/20

thank you very much sir

$${thank}\:{you}\:{very}\:{much}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com