
Question and Answers Forum
Question Number 116096 by mathmax by abdo last updated on 30/Sep/20
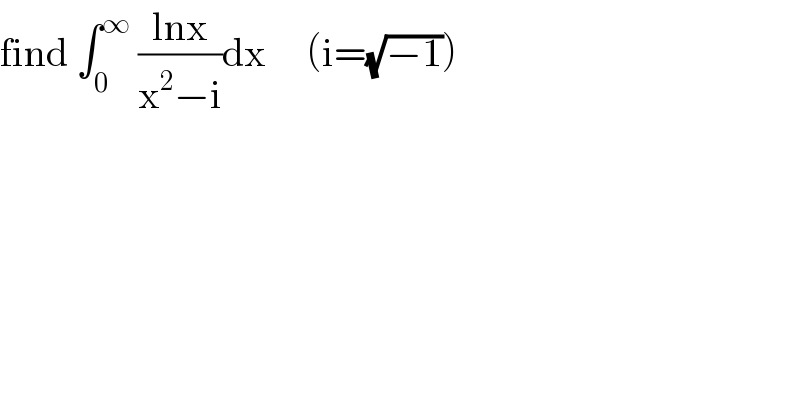
Answered by mindispower last updated on 01/Oct/20
![let f(z)=((ln(z))/(z^2 −i)) ln(z)=ln∣z∣+iarg(z),arg(z)∈]−(π/2),((3π)/2)[ C_R =∪_(a≤R) {ae^(iθ) ∈[0,π]} pol of ((ln(z))/(z^2 −i)) are ((1+i)/( (√2))),−((1+i)/( (√2))) ∫_C_R f(z)dz=2iπRes(f,((1+i)/( (√2)))), whenR≥1 ∫_C_R f(z)dz=∫_(−R) ^0 f(z)dz+∫_0 ^R f(z)dz+∫_(Re^(iθ) ) f(z)dz ∫_(−R) ^0 f(z)dz=∫_0 ^R f(−z)dz=∫_0 ^R ((ln(−z))/(z^2 −i))dz =∫_0 ^R ((ln(z)+iπ)/(z^2 −i))dz ∫_(Re^(iθ) ) f(z)dz=∫_0 ^π f(Re^(iθ) ).iRe^(iθ) dθ =∫_0 ^π ((ln(R)+iθ)/(R^2 e^(2iθ) −i)).iRe^(iθ) dθ ∣((ln(R)+iθ)/(R^2 e^(2iθ) −i)).iRe^(iθ) ∣≤((R(√(ln^2 (R)+π^2 )))/(∣R^2 −1∣))→0 when R→0 ⇒lim_(R→∞) ∫_C_R f(z)dz=2iπRes(f,((1+i)/( (√2)))) =2∫_0 ^∞ ((ln(z))/(z^2 −i))dz+∫_0 ^∞ ((iπdz)/(z^2 −i))=2iπ.((ln(e^(i(π/4)) ))/(2.e^(i(π/4)) )) =2iπ.((iπ)/4).(1/( (√2)(1+i)))=−((π^2 (1−i))/(4(√2))) ∫_0 ^∞ ((iπ)/(z^2 −i))=∫_0 ^∞ (i/(2e^(i(π/4)) ))π.((1/(z−e^(i(π/4)) ))−(1/(z+e^(i(π/4)) )))dz =i(π/(2e^(i(π/4)) ))lim_(R→∞) [ln(((R−e^(i(π/4)) )/(R+e^(i(π/4)) )))−ln(−1)) =((iπ)/(2e^(i(π/4)) )).−iπ=(π^2 /(2e^(i(π/4)) )) ⇔2∫_0 ^∞ ((ln(z))/(z^2 −i))=−(π^2 /4)e^(−i(π/4)) −(π^2 /2)e^(−i(π/4)) ⇒∫_0 ^∞ ((ln(z))/(z^2 −i))dz=((−3π^2 )/8)(((1−i)/( (√2))))](Q116156.png)
Commented by 1549442205PVT last updated on 01/Oct/20

| ||
Question and Answers Forum | ||
Question Number 116096 by mathmax by abdo last updated on 30/Sep/20 | ||
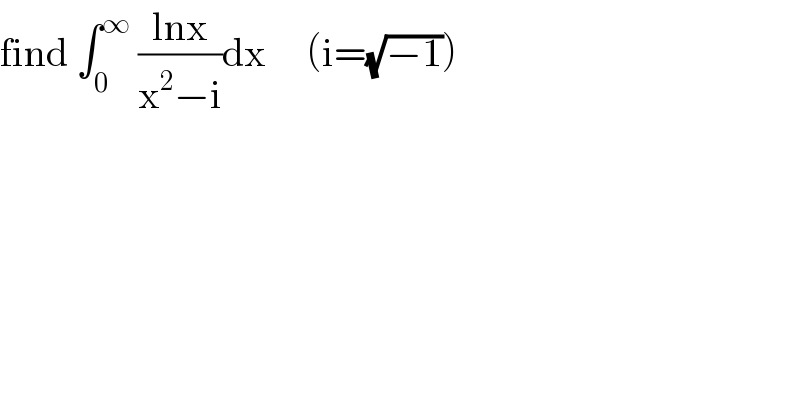 | ||
Answered by mindispower last updated on 01/Oct/20 | ||
![let f(z)=((ln(z))/(z^2 −i)) ln(z)=ln∣z∣+iarg(z),arg(z)∈]−(π/2),((3π)/2)[ C_R =∪_(a≤R) {ae^(iθ) ∈[0,π]} pol of ((ln(z))/(z^2 −i)) are ((1+i)/( (√2))),−((1+i)/( (√2))) ∫_C_R f(z)dz=2iπRes(f,((1+i)/( (√2)))), whenR≥1 ∫_C_R f(z)dz=∫_(−R) ^0 f(z)dz+∫_0 ^R f(z)dz+∫_(Re^(iθ) ) f(z)dz ∫_(−R) ^0 f(z)dz=∫_0 ^R f(−z)dz=∫_0 ^R ((ln(−z))/(z^2 −i))dz =∫_0 ^R ((ln(z)+iπ)/(z^2 −i))dz ∫_(Re^(iθ) ) f(z)dz=∫_0 ^π f(Re^(iθ) ).iRe^(iθ) dθ =∫_0 ^π ((ln(R)+iθ)/(R^2 e^(2iθ) −i)).iRe^(iθ) dθ ∣((ln(R)+iθ)/(R^2 e^(2iθ) −i)).iRe^(iθ) ∣≤((R(√(ln^2 (R)+π^2 )))/(∣R^2 −1∣))→0 when R→0 ⇒lim_(R→∞) ∫_C_R f(z)dz=2iπRes(f,((1+i)/( (√2)))) =2∫_0 ^∞ ((ln(z))/(z^2 −i))dz+∫_0 ^∞ ((iπdz)/(z^2 −i))=2iπ.((ln(e^(i(π/4)) ))/(2.e^(i(π/4)) )) =2iπ.((iπ)/4).(1/( (√2)(1+i)))=−((π^2 (1−i))/(4(√2))) ∫_0 ^∞ ((iπ)/(z^2 −i))=∫_0 ^∞ (i/(2e^(i(π/4)) ))π.((1/(z−e^(i(π/4)) ))−(1/(z+e^(i(π/4)) )))dz =i(π/(2e^(i(π/4)) ))lim_(R→∞) [ln(((R−e^(i(π/4)) )/(R+e^(i(π/4)) )))−ln(−1)) =((iπ)/(2e^(i(π/4)) )).−iπ=(π^2 /(2e^(i(π/4)) )) ⇔2∫_0 ^∞ ((ln(z))/(z^2 −i))=−(π^2 /4)e^(−i(π/4)) −(π^2 /2)e^(−i(π/4)) ⇒∫_0 ^∞ ((ln(z))/(z^2 −i))dz=((−3π^2 )/8)(((1−i)/( (√2))))](Q116156.png) | ||
| ||
Commented by 1549442205PVT last updated on 01/Oct/20 | ||
 | ||