
Question and Answers Forum
Question Number 116112 by Lordose last updated on 01/Oct/20
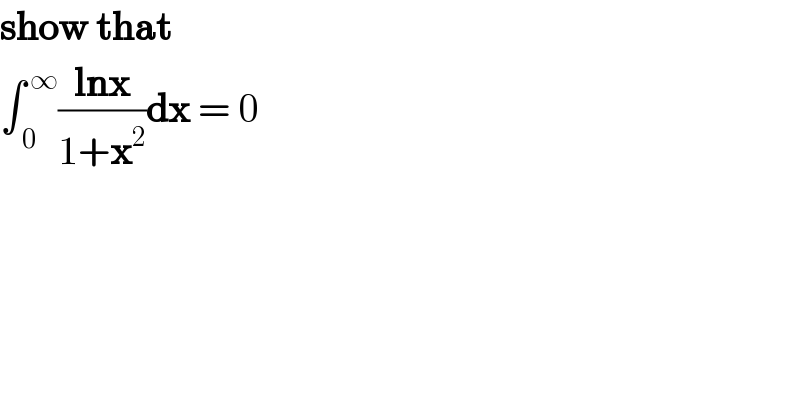
Answered by MJS_new last updated on 01/Oct/20
![∫_0 ^1 ((ln x)/(1+x^2 ))dx= [t=(1/x) → dx=−x^2 dt=−(dt/t^2 )] =∫_∞ ^1 ((ln (1/t))/(1+(1/t^2 )))×−(dt/t^2 )= [ln (1/t) =−ln t ∧ −∫_a ^b f(t)dt=∫_b ^a f(t)dt] =−∫_1 ^∞ ((ln t)/(1+t^2 ))dt ⇒ ∫_0 ^1 ((ln x)/(1+x^2 ))=−∫_1 ^∞ ((ln x)/(1+x^2 ))dx ∫_0 ^1 ((ln x)/(1+x^2 ))+∫_1 ^∞ ((ln x)/(1+x^2 ))dx=0 ⇔ ∫_0 ^∞ ((ln x)/(1+x^2 ))dx=0 [∫_a ^b f(x)dx+∫_b ^c f(x)dx=∫_a ^c f(x)dx]](Q116121.png)
Answered by Bird last updated on 02/Oct/20
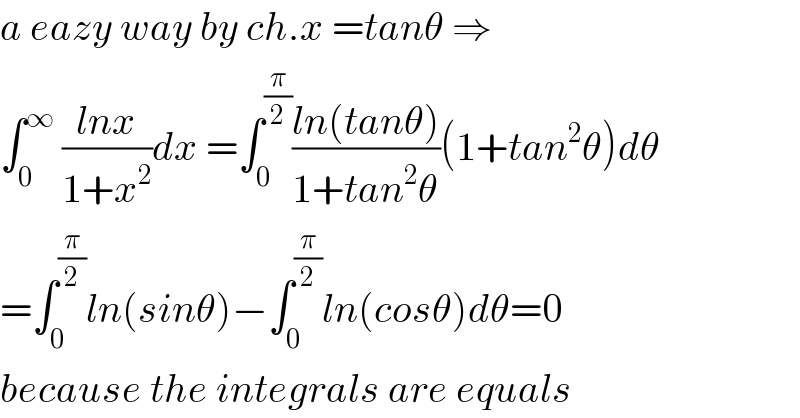
| ||
Question and Answers Forum | ||
Question Number 116112 by Lordose last updated on 01/Oct/20 | ||
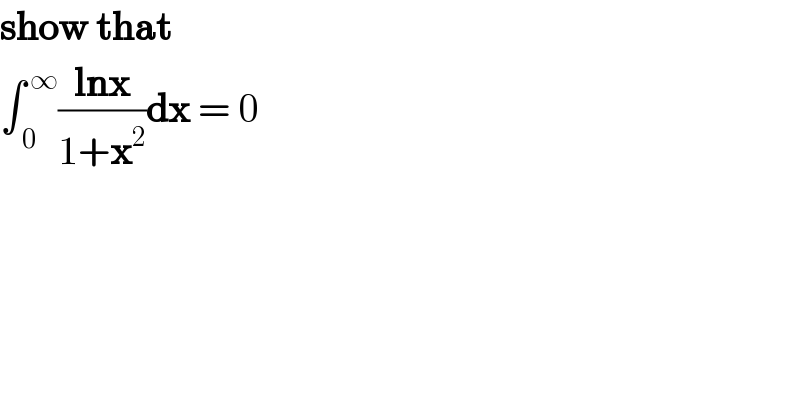 | ||
Answered by MJS_new last updated on 01/Oct/20 | ||
![∫_0 ^1 ((ln x)/(1+x^2 ))dx= [t=(1/x) → dx=−x^2 dt=−(dt/t^2 )] =∫_∞ ^1 ((ln (1/t))/(1+(1/t^2 )))×−(dt/t^2 )= [ln (1/t) =−ln t ∧ −∫_a ^b f(t)dt=∫_b ^a f(t)dt] =−∫_1 ^∞ ((ln t)/(1+t^2 ))dt ⇒ ∫_0 ^1 ((ln x)/(1+x^2 ))=−∫_1 ^∞ ((ln x)/(1+x^2 ))dx ∫_0 ^1 ((ln x)/(1+x^2 ))+∫_1 ^∞ ((ln x)/(1+x^2 ))dx=0 ⇔ ∫_0 ^∞ ((ln x)/(1+x^2 ))dx=0 [∫_a ^b f(x)dx+∫_b ^c f(x)dx=∫_a ^c f(x)dx]](Q116121.png) | ||
| ||
Answered by Bird last updated on 02/Oct/20 | ||
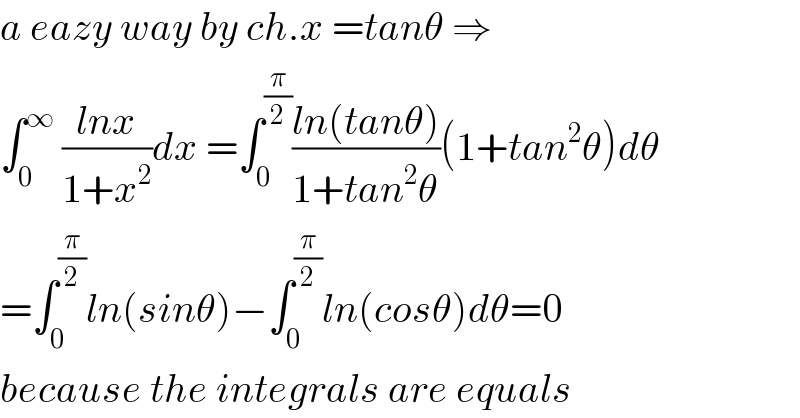 | ||
| ||