Question Number 116284 by mnjuly1970 last updated on 02/Oct/20
$$\:\:\:\:\:\:\:\:\:\:\:\:\:...\:\:{calculus}\:{I}\:... \\ $$$$\:\:\:\:\:{evaluate}\::\: \\ $$$$ \\ $$$$\:\:\:\:\:\mathrm{I}\::=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{3}}} {log}\left(\mathrm{1}+\sqrt{\mathrm{3}}\:{tan}\left({x}\right)\right){dx}=??? \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$
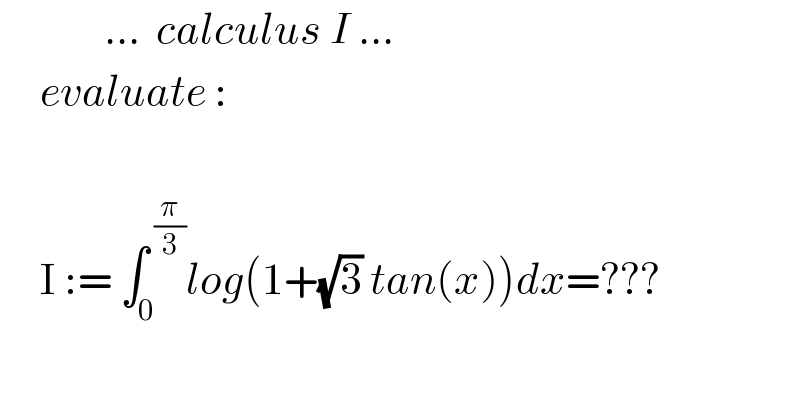
Answered by Dwaipayan Shikari last updated on 02/Oct/20
![I=∫_0 ^(π/3) log(cosx+(√3)sinx)−log(cosx)dx =[∫_0 ^(π/3) log(sin((π/6)+x))−log(cosx)]→(I_0 )+∫_0 ^(π/3) log(2)dx =[∫_0 ^(π/3) log(sinx((π/2)−x))−log(cos((π/3)−x))]→(I_0 )+(π/3)log(2) 2I_0 =∫_0 ^(π/3) log(cosx)−log(cosx)+(1/2)cosx−(1/2)cosx+((√3)/2)sinx−((√3)/2)sinx I_0 =0 So I=I_0 +(π/3)log(2) I=(π/3)log(2)](Q116287.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \mathrm{log}\left(\mathrm{cosx}+\sqrt{\mathrm{3}}\mathrm{sinx}\right)−\mathrm{log}\left(\mathrm{cosx}\right)\mathrm{dx} \\ $$$$\:\:\:=\left[\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \mathrm{log}\left(\mathrm{sin}\left(\frac{\pi}{\mathrm{6}}+\mathrm{x}\right)\right)−\mathrm{log}\left(\mathrm{cosx}\right)\right]\rightarrow\left(\mathrm{I}_{\mathrm{0}} \right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \mathrm{log}\left(\mathrm{2}\right)\mathrm{dx} \\ $$$$=\left[\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \mathrm{log}\left(\mathrm{sinx}\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)\right)−\mathrm{log}\left(\mathrm{cos}\left(\frac{\pi}{\mathrm{3}}−\mathrm{x}\right)\right)\right]\rightarrow\left(\mathrm{I}_{\mathrm{0}} \right)+\frac{\pi}{\mathrm{3}}\mathrm{log}\left(\mathrm{2}\right) \\ $$$$\mathrm{2I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \mathrm{log}\left(\mathrm{cosx}\right)−\mathrm{log}\left(\mathrm{cosx}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cosx}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cosx}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sinx}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sinx} \\ $$$$\mathrm{I}_{\mathrm{0}} =\mathrm{0} \\ $$$$\mathrm{So} \\ $$$$\mathrm{I}=\mathrm{I}_{\mathrm{0}} +\frac{\pi}{\mathrm{3}}\mathrm{log}\left(\mathrm{2}\right) \\ $$$$\mathrm{I}=\frac{\pi}{\mathrm{3}}\mathrm{log}\left(\mathrm{2}\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 02/Oct/20
$${nice}\:{very}\:{nice}\:{as} \\ $$$${always}...{thank}\:{you}... \\ $$
Commented by Dwaipayan Shikari last updated on 02/Oct/20
��
Answered by mnjuly1970 last updated on 02/Oct/20
$$\:\:\:\:\mathrm{I}\overset{\int_{\mathrm{0}} ^{\:{a}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\:{a}} {f}\left({a}−{x}\right){dx}} {=}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{3}}} {log}\left(\mathrm{1}+\sqrt{\mathrm{3}\:}\:\left(\frac{\sqrt{\mathrm{3}}−{tan}\left({x}\right)}{\:\mathrm{1}+\sqrt{\mathrm{3}}{tan}\left({x}\right)}\right)\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{3}}} {log}\left(\frac{\mathrm{4}}{\mathrm{1}+\sqrt{\mathrm{3}}{tan}\left({x}\right)}\right){dx}=\frac{\pi}{\mathrm{3}}{log}\left(\mathrm{4}\right)−\mathrm{I} \\ $$$$ \\ $$$$\therefore\:\:\mathrm{I}\:=\frac{\pi}{\mathrm{3}}\:{log}\left(\mathrm{2}\right)\:\:...\checkmark \\ $$$$\:\:\:\:\:\:{m}.{n}.\mathrm{1970} \\ $$
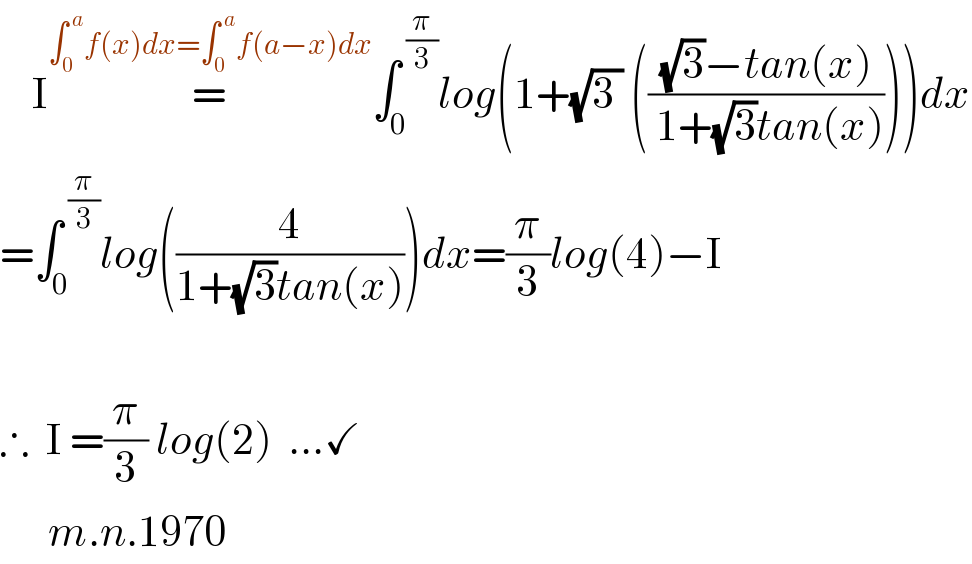
Answered by Bird last updated on 03/Oct/20
![let g(a) =∫_0 ^(π/3) ln(1+atanx)dx ⇒ g^′ (a) =∫_0 ^(π/3) ((tanx)/(1+atanx))dx =(1/a)∫_0 ^(π/3) ((1+atanx−1)/(1+atanx)) dx =(π/(3a)) −(1/a)∫_0 ^(π/3) (dx/(1+atanx)) but ∫_0 ^(π/3) (dx/(1+atanx)) =_(tanx=t) ∫_0 ^(√3) (dt/((1+t^2 )(1+at))) let decompose F(t) =(1/((at+1)(t^2 +1))) F(t) =(α/(at+1)) +((mt+n)/(t^2 +1)) α =(1/((1/a^2 )+1)) =(a^2 /(1+a^2 )) lim_(t→+∞) tF(t) =0 =(α/a) +m ⇒ m=−(α/a) =−(a/(1+a^2 )) F(0)=1 =α +n ⇒n=1−α =1−(a^2 /(1+a^2 )) =(1/(1+a^2 )) ⇒F(t)=(a^2 /((1+a^2 )(at+1)))+((−(a/(1+a^2 ))t+(1/(1+a^2 )))/(t^2 +1)) ⇒∫_0 ^(π/3) (dx/(1+atanx)) =(a^2 /(1+a^2 ))∫_0 ^(√3) (dt/(at +1))−(a/(1+a^2 ))∫_0 ^(√3) (t/(t^2 +1))dt +(1/(1+a^2 )) ∫_0 ^(√3) (dt/(1+t^2 )) =(a/(1+a^2 ))[ln(at+1)]_0 ^(√3) −(a/(2(1+a^2 )))[ln(1+t^2 )]_0 ^(√3) +(1/(1+a^2 ))×(π/3) =(a/(1+a^2 ))ln(a(√3)+1)−(a/((1+a^2 )))ln2 +(π/(3(1+a^2 )))](Q116314.png)
$${let}\:{g}\left({a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} {ln}\left(\mathrm{1}+{atanx}\right){dx}\:\Rightarrow \\ $$$${g}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:\:\frac{{tanx}}{\mathrm{1}+{atanx}}{dx} \\ $$$$=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{1}+{atanx}−\mathrm{1}}{\mathrm{1}+{atanx}}\:{dx} \\ $$$$=\frac{\pi}{\mathrm{3}{a}}\:−\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \frac{{dx}}{\mathrm{1}+{atanx}}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{{dx}}{\mathrm{1}+{atanx}}\:=_{{tanx}={t}} \:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{at}\right)} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)\:=\frac{\mathrm{1}}{\left({at}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$${F}\left({t}\right)\:=\frac{\alpha}{{at}+\mathrm{1}}\:+\frac{{mt}+{n}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\alpha\:=\frac{\mathrm{1}}{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\mathrm{1}}\:=\frac{{a}^{\mathrm{2}} }{\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$${lim}_{{t}\rightarrow+\infty} {tF}\left({t}\right)\:=\mathrm{0}\:=\frac{\alpha}{{a}}\:+{m}\:\Rightarrow \\ $$$${m}=−\frac{\alpha}{{a}}\:=−\frac{{a}}{\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{1}\:=\alpha\:+{n}\:\Rightarrow{n}=\mathrm{1}−\alpha \\ $$$$=\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{1}+{a}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{F}\left({t}\right)=\frac{{a}^{\mathrm{2}} }{\left(\mathrm{1}+{a}^{\mathrm{2}} \right)\left({at}+\mathrm{1}\right)}+\frac{−\frac{{a}}{\mathrm{1}+{a}^{\mathrm{2}} }{t}+\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} }}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{{dx}}{\mathrm{1}+{atanx}} \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{1}+{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:\frac{{dt}}{{at}\:+\mathrm{1}}−\frac{{a}}{\mathrm{1}+{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$+\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\frac{{a}}{\mathrm{1}+{a}^{\mathrm{2}} }\left[{ln}\left({at}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} −\frac{{a}}{\mathrm{2}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)}\left[{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} }×\frac{\pi}{\mathrm{3}} \\ $$$$=\frac{{a}}{\mathrm{1}+{a}^{\mathrm{2}} }{ln}\left({a}\sqrt{\mathrm{3}}+\mathrm{1}\right)−\frac{{a}}{\left(\mathrm{1}+{a}^{\mathrm{2}} \right)}{ln}\mathrm{2} \\ $$$$+\frac{\pi}{\mathrm{3}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)} \\ $$
Commented by Bird last updated on 03/Oct/20
$$\Rightarrow{g}^{'} \left({a}\right)\:=\frac{\pi}{\mathrm{3}{a}}−\frac{\mathrm{1}}{{a}}\left\{\frac{{a}}{\mathrm{1}+{a}^{\mathrm{2}} }{ln}\left({a}\sqrt{\mathrm{3}}+\mathrm{1}\right)\right. \\ $$$$\left.−\frac{{aln}\mathrm{2}}{\mathrm{1}+{a}^{\mathrm{2}} }+\frac{\pi}{\mathrm{3}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)}\right\} \\ $$$$=\frac{\pi}{\mathrm{3}{a}}−\frac{{ln}\left({a}\sqrt{\mathrm{3}}+\mathrm{1}\right)}{\mathrm{1}+{a}^{\mathrm{2}} }\:+\frac{{ln}\mathrm{2}}{\mathrm{1}+{a}^{\mathrm{2}} }−\frac{\pi}{\mathrm{3}{a}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow{g}\left({a}\right)\:=\frac{\pi}{\mathrm{3}}{lna}−\int\frac{{ln}\left({a}\sqrt{\mathrm{3}}+\mathrm{1}\right)}{\mathrm{1}+{a}^{\mathrm{2}} }{da} \\ $$$$+{ln}\mathrm{2}\:{arctana}−\frac{\pi}{\mathrm{3}}\int\:\:\frac{{da}}{{a}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)} \\ $$$$...{be}\:{continued}... \\ $$