
Question and Answers Forum
Question Number 116311 by bemath last updated on 03/Oct/20
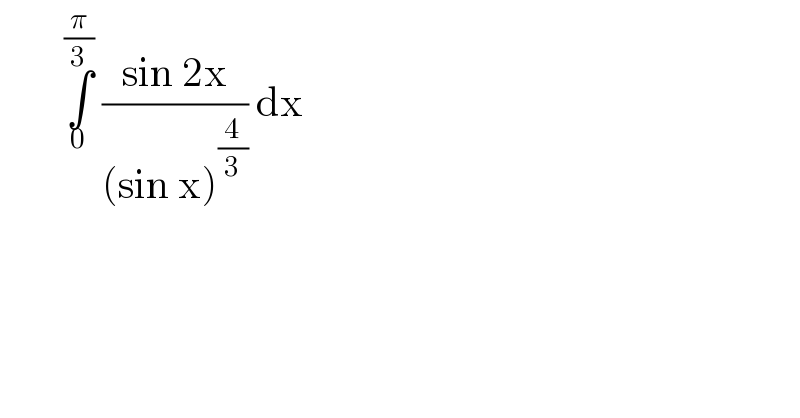
Answered by bobhans last updated on 03/Oct/20
![let sin x = u with { ((u=((√3)/2))),((u=0)) :} I = ∫_0 ^((√3)/2) ((2u du)/u^(4/3) ) = 2∫_0 ^((√3)/2) u^(−(1/3)) du I= 2[ (3/2)u^(2/3) ]_0 ^((√3)/2) = 3(((√3)/2))^(2/3) =3((3/4))^(1/(3 )) = 3 ((6/8))^(1/(3 )) = ((3 (6)^(1/(3 )) )/2) .](Q116312.png)
Answered by Bird last updated on 03/Oct/20
![I =∫_0 ^(π/3) ((2sinx cosx)/((sinx)^(4/3) ))dx =_(sinx=t) 2∫_0 ^((√3)/2) ((t(√(1−t^2 )))/t^(4/3) )(dt/( (√(1−t^2 )))) =2 ∫_0 ^((√3)/2) t^(1−(4/3)) dt =2 ∫_0 ^((√3)/2) t^(−(1/3)) dt =2[(1/(1−(1/3)))t^(1−(1/3)) ]_0 ^((√3)/2) =2[(3/2)t^(2/3) ]_0 ^((√3)/2) =3((((√3)/2))^(2/3) ) =3(^3 (√(3/4)))](Q116313.png)
Answered by Dwaipayan Shikari last updated on 03/Oct/20
![∫_0 ^(π/3) ((sin2x)/((sinx)^(4/3) ))dx ∫_0 ^(π/3) ((2cosx)/(sin^(1/3) x))dx =2∫_0 ^((√3)/2) (dt/t^(1/3) )=3[t^(2/3) ]^((√3)/2) =3(((√3)/2))^(2/3) =3^(4/3) ((1/2))^(2/3)](Q116337.png)
| ||
Question and Answers Forum | ||
Question Number 116311 by bemath last updated on 03/Oct/20 | ||
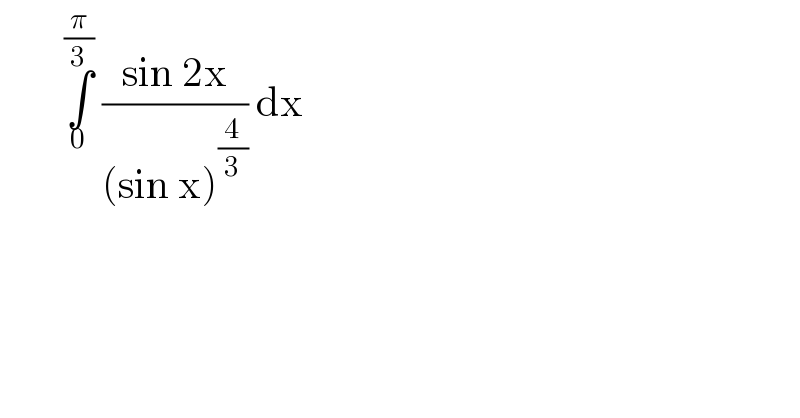 | ||
Answered by bobhans last updated on 03/Oct/20 | ||
![let sin x = u with { ((u=((√3)/2))),((u=0)) :} I = ∫_0 ^((√3)/2) ((2u du)/u^(4/3) ) = 2∫_0 ^((√3)/2) u^(−(1/3)) du I= 2[ (3/2)u^(2/3) ]_0 ^((√3)/2) = 3(((√3)/2))^(2/3) =3((3/4))^(1/(3 )) = 3 ((6/8))^(1/(3 )) = ((3 (6)^(1/(3 )) )/2) .](Q116312.png) | ||
| ||
Answered by Bird last updated on 03/Oct/20 | ||
![I =∫_0 ^(π/3) ((2sinx cosx)/((sinx)^(4/3) ))dx =_(sinx=t) 2∫_0 ^((√3)/2) ((t(√(1−t^2 )))/t^(4/3) )(dt/( (√(1−t^2 )))) =2 ∫_0 ^((√3)/2) t^(1−(4/3)) dt =2 ∫_0 ^((√3)/2) t^(−(1/3)) dt =2[(1/(1−(1/3)))t^(1−(1/3)) ]_0 ^((√3)/2) =2[(3/2)t^(2/3) ]_0 ^((√3)/2) =3((((√3)/2))^(2/3) ) =3(^3 (√(3/4)))](Q116313.png) | ||
| ||
Answered by Dwaipayan Shikari last updated on 03/Oct/20 | ||
![∫_0 ^(π/3) ((sin2x)/((sinx)^(4/3) ))dx ∫_0 ^(π/3) ((2cosx)/(sin^(1/3) x))dx =2∫_0 ^((√3)/2) (dt/t^(1/3) )=3[t^(2/3) ]^((√3)/2) =3(((√3)/2))^(2/3) =3^(4/3) ((1/2))^(2/3)](Q116337.png) | ||
| ||