
Question and Answers Forum
Question Number 116318 by Bird last updated on 03/Oct/20
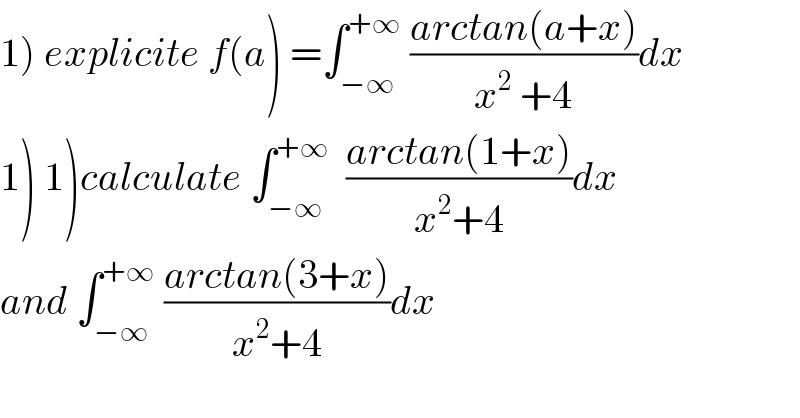
Answered by Olaf last updated on 03/Oct/20
![1) F(x) = ∫_a ^b f(x,t)dt ⇒ F′(x) = ∫_a ^b (∂f/∂x)(x,t)dt Here we have : f′(a) = ∫_(−∞) ^(+∞) (1/(x^2 +4))×(1/((a+x)^2 +1))dx f′(a) = ∫_(−∞) ^(+∞) [((Ax+B)/(x^2 +4))+((C(x+a)+D)/((x+a)^2 +1))]dx A = −((2a)/((a^2 +1)(a^2 +9))) B = ((a^2 −3)/((a^2 +1)(a^2 +9))) C = ((2a)/((a^2 +1)(a^2 +9))) = −A D = ((a^2 +3)/((a^2 +1)(a^2 +9))) f′(a) = (A/2)[ln∣((x^2 +4)/((x+a)^2 +1))∣]_(−∞) ^(+∞) +(B/2)[arctan((x/2))]_(−∞) ^(+∞) +D[arctan(x+a)]_(−∞) ^(+∞) f′(a) = (π/2)B+πD f′(a) = ((3π)/2).(1/(a^2 +9)) ⇒ f(a) = (π/2)arctan(a/3)+K lim_(a→+∞) f(a) = (π^2 /4)+K and lim_(a→+∞) f(a) = ∫_(−∞) ^(+∞) (π/2).(1/(x^2 +4))dx lim_(a→+∞) f(a) = (π/4)[arctan(x/2)]_(−∞) ^(+∞) = (π^2 /4) ⇒ (π^2 /4)+K = (π^2 /4), K = 0 Finally f(a) = (π/2)arctan(a/3) 1)1) ∫_(−∞) ^(+∞) ((arctan(1+x))/(x^2 +4))dx = f(1) = (π/2)arctan(1/3) (arctan(1/3) = 0,322...) ∫_(−∞) ^(+∞) ((arctan(3+x))/(x^2 +4))dx = f(3) = (π/2)arctan(1) ∫_(−∞) ^(+∞) ((arctan(3+x))/(x^2 +4))dx = f(3) = (π^2 /8) Please verify my calculous...](Q116340.png)
Commented by mathmax by abdo last updated on 03/Oct/20

| ||
Question and Answers Forum | ||
Question Number 116318 by Bird last updated on 03/Oct/20 | ||
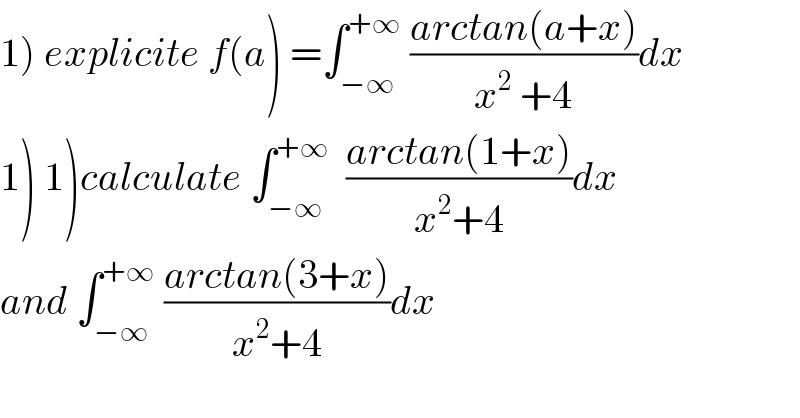 | ||
Answered by Olaf last updated on 03/Oct/20 | ||
![1) F(x) = ∫_a ^b f(x,t)dt ⇒ F′(x) = ∫_a ^b (∂f/∂x)(x,t)dt Here we have : f′(a) = ∫_(−∞) ^(+∞) (1/(x^2 +4))×(1/((a+x)^2 +1))dx f′(a) = ∫_(−∞) ^(+∞) [((Ax+B)/(x^2 +4))+((C(x+a)+D)/((x+a)^2 +1))]dx A = −((2a)/((a^2 +1)(a^2 +9))) B = ((a^2 −3)/((a^2 +1)(a^2 +9))) C = ((2a)/((a^2 +1)(a^2 +9))) = −A D = ((a^2 +3)/((a^2 +1)(a^2 +9))) f′(a) = (A/2)[ln∣((x^2 +4)/((x+a)^2 +1))∣]_(−∞) ^(+∞) +(B/2)[arctan((x/2))]_(−∞) ^(+∞) +D[arctan(x+a)]_(−∞) ^(+∞) f′(a) = (π/2)B+πD f′(a) = ((3π)/2).(1/(a^2 +9)) ⇒ f(a) = (π/2)arctan(a/3)+K lim_(a→+∞) f(a) = (π^2 /4)+K and lim_(a→+∞) f(a) = ∫_(−∞) ^(+∞) (π/2).(1/(x^2 +4))dx lim_(a→+∞) f(a) = (π/4)[arctan(x/2)]_(−∞) ^(+∞) = (π^2 /4) ⇒ (π^2 /4)+K = (π^2 /4), K = 0 Finally f(a) = (π/2)arctan(a/3) 1)1) ∫_(−∞) ^(+∞) ((arctan(1+x))/(x^2 +4))dx = f(1) = (π/2)arctan(1/3) (arctan(1/3) = 0,322...) ∫_(−∞) ^(+∞) ((arctan(3+x))/(x^2 +4))dx = f(3) = (π/2)arctan(1) ∫_(−∞) ^(+∞) ((arctan(3+x))/(x^2 +4))dx = f(3) = (π^2 /8) Please verify my calculous...](Q116340.png) | ||
| ||
Commented by mathmax by abdo last updated on 03/Oct/20 | ||
 | ||