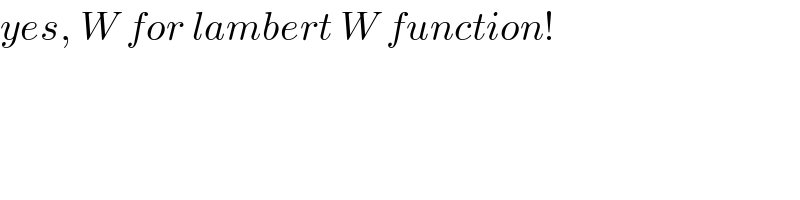Previous in Differential Equation Next in Differential Equation
Question Number 116329 by bemath last updated on 03/Oct/20
$$\mathrm{solve}\:\mathrm{the}\:\mathrm{diff}\:\mathrm{equation}\:\: \\ $$$$\left(\mathrm{1}\right)\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{x}+\mathrm{3y}−\mathrm{5}}{\mathrm{x}−\mathrm{y}−\mathrm{1}} \\ $$$$\left(\mathrm{2}\right)\:\left(\mathrm{3y}−\mathrm{7x}−\mathrm{3}\right)\mathrm{dx}+\left(\mathrm{7y}−\mathrm{3x}−\mathrm{7}\right)\mathrm{dy}=\mathrm{0} \\ $$
Answered by mr W last updated on 03/Oct/20
![(1) (dy/dx)=((x+3y−5)/(x−y−1)) let x=u+a y=v+b ⇒x+3y−5=u+3v+a+3b−5 ⇒x−y−1=u−v+a−b−1 a+3b−5=0 ...(i) a−b−1=0 ...(ii) ⇒a=2 ⇒b=1 ⇒x=u+2 ⇒y=v+1 (dy/dx)=(dv/du)=((u+3v)/(u−v)) v=tu (dv/du)=t+u(dt/du)=((1+3t)/(1−t)) u(dt/du)=((1+3t)/(1−t))−t=(((1+t)^2 )/(1−t)) ⇒(((1−t)dt)/((1+t)^2 ))=(du/u) ⇒[(2/((1+t)^2 ))−(1/(1+t))]dt=(du/u) ⇒−(2/(1+t))−ln (1+t)=ln u+C ⇒ln u(1+t)=−((2/(1+t))+C) ⇒u(1+t)=Ce^(−(2/(1+t))) ⇒(x−2)(1+((y−1)/(x−2)))=Ce^(−(2/(1+((y−1)/(x−2))))) ⇒x+y−3=Ce^(−((2(x−2))/(x+y−3))) ⇒C(x−2)=((−2(x−2))/(x+y−3))e^(−((2(x−2))/(x+y−3))) ⇒((−2(x−2))/(x+y−3))=W(C(x−2)) ⇒y=3−((2(x−2))/(W(C(x−2))))−x](Q116335.png)
$$\left(\mathrm{1}\right)\:\:\frac{{dy}}{{dx}}=\frac{{x}+\mathrm{3}{y}−\mathrm{5}}{{x}−{y}−\mathrm{1}} \\ $$$${let} \\ $$$${x}={u}+{a} \\ $$$${y}={v}+{b} \\ $$$$\Rightarrow{x}+\mathrm{3}{y}−\mathrm{5}={u}+\mathrm{3}{v}+{a}+\mathrm{3}{b}−\mathrm{5} \\ $$$$\Rightarrow{x}−{y}−\mathrm{1}={u}−{v}+{a}−{b}−\mathrm{1} \\ $$$${a}+\mathrm{3}{b}−\mathrm{5}=\mathrm{0}\:\:\:...\left({i}\right) \\ $$$${a}−{b}−\mathrm{1}=\mathrm{0}\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow{a}=\mathrm{2} \\ $$$$\Rightarrow{b}=\mathrm{1} \\ $$$$\Rightarrow{x}={u}+\mathrm{2} \\ $$$$\Rightarrow{y}={v}+\mathrm{1} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dv}}{{du}}=\frac{{u}+\mathrm{3}{v}}{{u}−{v}} \\ $$$${v}={tu} \\ $$$$\frac{{dv}}{{du}}={t}+{u}\frac{{dt}}{{du}}=\frac{\mathrm{1}+\mathrm{3}{t}}{\mathrm{1}−{t}} \\ $$$${u}\frac{{dt}}{{du}}=\frac{\mathrm{1}+\mathrm{3}{t}}{\mathrm{1}−{t}}−{t}=\frac{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{\mathrm{1}−{t}} \\ $$$$\Rightarrow\frac{\left(\mathrm{1}−{t}\right){dt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }=\frac{{du}}{{u}} \\ $$$$\Rightarrow\left[\frac{\mathrm{2}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right]{dt}=\frac{{du}}{{u}} \\ $$$$\Rightarrow−\frac{\mathrm{2}}{\mathrm{1}+{t}}−\mathrm{ln}\:\left(\mathrm{1}+{t}\right)=\mathrm{ln}\:{u}+{C} \\ $$$$\Rightarrow\mathrm{ln}\:{u}\left(\mathrm{1}+{t}\right)=−\left(\frac{\mathrm{2}}{\mathrm{1}+{t}}+{C}\right) \\ $$$$\Rightarrow{u}\left(\mathrm{1}+{t}\right)={Ce}^{−\frac{\mathrm{2}}{\mathrm{1}+{t}}} \\ $$$$\Rightarrow\left({x}−\mathrm{2}\right)\left(\mathrm{1}+\frac{{y}−\mathrm{1}}{{x}−\mathrm{2}}\right)={Ce}^{−\frac{\mathrm{2}}{\mathrm{1}+\frac{{y}−\mathrm{1}}{{x}−\mathrm{2}}}} \\ $$$$\Rightarrow{x}+{y}−\mathrm{3}={Ce}^{−\frac{\mathrm{2}\left({x}−\mathrm{2}\right)}{{x}+{y}−\mathrm{3}}} \\ $$$$\Rightarrow{C}\left({x}−\mathrm{2}\right)=\frac{−\mathrm{2}\left({x}−\mathrm{2}\right)}{{x}+{y}−\mathrm{3}}{e}^{−\frac{\mathrm{2}\left({x}−\mathrm{2}\right)}{{x}+{y}−\mathrm{3}}} \\ $$$$\Rightarrow\frac{−\mathrm{2}\left({x}−\mathrm{2}\right)}{{x}+{y}−\mathrm{3}}=\mathbb{W}\left({C}\left({x}−\mathrm{2}\right)\right) \\ $$$$\Rightarrow{y}=\mathrm{3}−\frac{\mathrm{2}\left({x}−\mathrm{2}\right)}{\mathbb{W}\left({C}\left({x}−\mathrm{2}\right)\right)}−{x} \\ $$
Commented by bemath last updated on 03/Oct/20
$$\mathrm{W}\:\mathrm{is}\:\mathrm{Lambert}\:\mathrm{W}\:\mathrm{Function}?\:\mathrm{thankyou} \\ $$$$\mathrm{sir} \\ $$
Commented by mr W last updated on 03/Oct/20
$${yes},\:{W}\:{for}\:{lambert}\:{W}\:{function}! \\ $$