Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 116385 by bemath last updated on 03/Oct/20

∫ ((xe^x )/( (√(1+e^x )))) dx

$$\:\int\:\frac{\mathrm{xe}^{\mathrm{x}} }{\:\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }}\:\mathrm{dx}\: \\ $$

Answered by MJS_new last updated on 03/Oct/20

∫((e^x x)/( (√(e^x +1))))dx= [t=(√(e^x +1)) → dx=((2(√(e^x +1)))/e^x )] =2∫ln (t^2 −1) dt=2∫ln (t−1) dt+2∫ln (t+1) dt= =2((t−1)ln (t−1) −t)+2((t+1)ln (t+1) −t)= =2tln (t^2 −1) +2ln ((t+1)/(t−1)) −4t= =2(x−2)(√(e^x +1))+2ln (e^x +2+2(√(e^x +1))) −2x+C

$$\int\frac{\mathrm{e}^{{x}} {x}}{\:\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{\mathrm{2}\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}}{\mathrm{e}^{{x}} }\right] \\ $$$$=\mathrm{2}\int\mathrm{ln}\:\left({t}^{\mathrm{2}} −\mathrm{1}\right)\:\mathrm{dt}=\mathrm{2}\int\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:{dt}+\mathrm{2}\int\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:{dt}= \\ $$$$=\mathrm{2}\left(\left({t}−\mathrm{1}\right)\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:−{t}\right)+\mathrm{2}\left(\left({t}+\mathrm{1}\right)\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:−{t}\right)= \\ $$$$=\mathrm{2}{t}\mathrm{ln}\:\left({t}^{\mathrm{2}} −\mathrm{1}\right)\:+\mathrm{2ln}\:\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}\:−\mathrm{4}{t}= \\ $$$$=\mathrm{2}\left({x}−\mathrm{2}\right)\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}+\mathrm{2ln}\:\left(\mathrm{e}^{{x}} +\mathrm{2}+\mathrm{2}\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}\right)\:−\mathrm{2}{x}+{C} \\ $$

Answered by Dwaipayan Shikari last updated on 03/Oct/20

∫((xe^x )/( (√(1+e^x ))))dx 1+e^x =t^2 ⇒e^x =2t(dt/dx) ∫((x2tdt)/t)=2∫xdt=2∫log(t^2 −1)dt 2tlog(t^2 −1)−∫((4t^2 )/(t^2 −1))dt 2tlog(t^2 −1)−4t+2log(((t+1)/(t−1)))+C 2x(√(e^x +1)) −4(√(e^x +1))+2log((((√(e^x +1))+1)/( (√(e^x +1))−1)))+C 2((√(e^x +1))(x−2)+log((((√(e^x +1))+1)/( (√(e^x +1))−1)))+C_1 )

$$\int\frac{\mathrm{xe}^{\mathrm{x}} }{\:\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }}\mathrm{dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}+\mathrm{e}^{\mathrm{x}} =\mathrm{t}^{\mathrm{2}} \Rightarrow\mathrm{e}^{\mathrm{x}} =\mathrm{2t}\frac{\mathrm{dt}}{\mathrm{dx}} \\ $$$$\int\frac{\mathrm{x2tdt}}{\mathrm{t}}=\mathrm{2}\int\mathrm{xdt}=\mathrm{2}\int\mathrm{log}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{dt} \\ $$$$\mathrm{2tlog}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)−\int\frac{\mathrm{4t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt} \\ $$$$\mathrm{2tlog}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{4t}+\mathrm{2log}\left(\frac{\mathrm{t}+\mathrm{1}}{\mathrm{t}−\mathrm{1}}\right)+\mathrm{C} \\ $$$$\mathrm{2x}\sqrt{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}\:−\mathrm{4}\sqrt{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}+\mathrm{2log}\left(\frac{\sqrt{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}+\mathrm{1}}{\:\sqrt{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}−\mathrm{1}}\right)+\mathrm{C} \\ $$$$\mathrm{2}\left(\sqrt{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}\left(\mathrm{x}−\mathrm{2}\right)+\mathrm{log}\left(\frac{\sqrt{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}+\mathrm{1}}{\:\sqrt{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}−\mathrm{1}}\right)+\mathrm{C}_{\mathrm{1}} \right) \\ $$

Commented by MJS_new last updated on 03/Oct/20

−∫((4t^2 )/(t^2 −1))dt=−4t+2ln ((t+1)/(t−1)) beside this minor error your result is the same as mine because (((√(e^x +1))+1)/( (√(e^x +1))−1))=((e^x +2+2(√(e^x +1)))/e^x ) ⇒ 2ln (((√(e^x +1))+1)/( (√(e^x +1))−1)) =−2x+2ln (e^x +2+2(√(e^x +1)))

$$−\int\frac{\mathrm{4}{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{1}}{dt}=−\mathrm{4}{t}+\mathrm{2ln}\:\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}} \\ $$$$\mathrm{beside}\:\mathrm{this}\:\mathrm{minor}\:\mathrm{error}\:\mathrm{your}\:\mathrm{result}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{same}\:\mathrm{as}\:\mathrm{mine}\:\mathrm{because} \\ $$$$\frac{\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}+\mathrm{1}}{\:\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}−\mathrm{1}}=\frac{\mathrm{e}^{{x}} +\mathrm{2}+\mathrm{2}\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}}{\mathrm{e}^{{x}} } \\ $$$$\Rightarrow \\ $$$$\mathrm{2ln}\:\frac{\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}+\mathrm{1}}{\:\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}−\mathrm{1}}\:=−\mathrm{2}{x}+\mathrm{2ln}\:\left(\mathrm{e}^{{x}} +\mathrm{2}+\mathrm{2}\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}\right) \\ $$

Commented by Dwaipayan Shikari last updated on 03/Oct/20

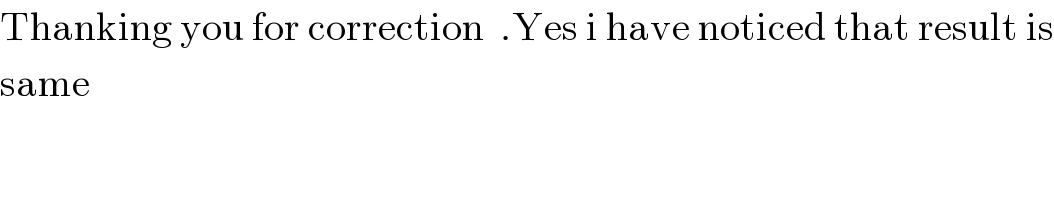
Thanking you for correction .Yes i have noticed that result is same

$$\mathrm{Thanking}\:\mathrm{you}\:\mathrm{for}\:\mathrm{correction}\:\:.\mathrm{Yes}\:\mathrm{i}\:\mathrm{have}\:\mathrm{noticed}\:\mathrm{that}\:\mathrm{result}\:\mathrm{is} \\ $$$$\mathrm{same} \\ $$

Answered by mathmax by abdo last updated on 03/Oct/20

I =∫ ((x e^x )/(√(1+e^x )))dx we do thechangement (√(1+e^x ))=t ⇒1+e^x =t^2 ⇒ e^x =t^2 −1 ⇒x =ln(t^2 −1) ⇒ I =∫ ((ln(t^2 −1)(t^2 −1))/t)×((2tdt)/(t^2 −1)) =2 ∫ln(t^2 −1)dt =_(by parts) 2{ t ln(t^2 −1)−∫ t.((2t)/(t^2 −1))dt} =2t ln(t^2 −1)−4 ∫ ((t^2 −1+1)/(t^2 −1))dt =2tln(t^2 −1)−4t −4 ∫ (dt/(t^2 −1)) =2tln(t^2 −1)−4t−2 ∫((1/(t−1))−(1/(t+1)))dt =2t ln(t^2 −1)−4t −2ln∣((t−1)/(t+1))∣ +c ⇒I =2x(√(1+e^x ))−4(√(1+e^x )) −2ln∣(((√(1+e^x ))−1)/((√(1+e^x ))+1))∣ +c

$$\mathrm{I}\:=\int\:\:\frac{\mathrm{x}\:\mathrm{e}^{\mathrm{x}} }{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{thechangement}\:\:\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }=\mathrm{t}\:\Rightarrow\mathrm{1}+\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow\mathrm{x}\:=\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\frac{\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{t}}×\frac{\mathrm{2tdt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\:=\mathrm{2}\:\int\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\boldsymbol{\mathrm{dt}} \\ $$$$=_{\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{parts}}} \:\:\:\:\:\mathrm{2}\left\{\:\boldsymbol{\mathrm{t}}\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{t}}^{\mathrm{2}} −\mathrm{1}\right)−\int\:\:\mathrm{t}.\frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}\right\} \\ $$$$=\mathrm{2t}\:\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{4}\:\int\:\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt} \\ $$$$=\mathrm{2tln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{4t}\:−\mathrm{4}\:\int\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\mathrm{2tln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{4t}−\mathrm{2}\:\int\left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)\mathrm{dt} \\ $$$$=\mathrm{2t}\:\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{4t}\:−\mathrm{2ln}\mid\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\mid\:+\mathrm{c} \\ $$$$\Rightarrow\mathrm{I}\:=\mathrm{2x}\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }−\mathrm{4}\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\:−\mathrm{2ln}\mid\frac{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }−\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }+\mathrm{1}}\mid\:+\mathrm{c} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com