Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 116391 by bobhans last updated on 03/Oct/20

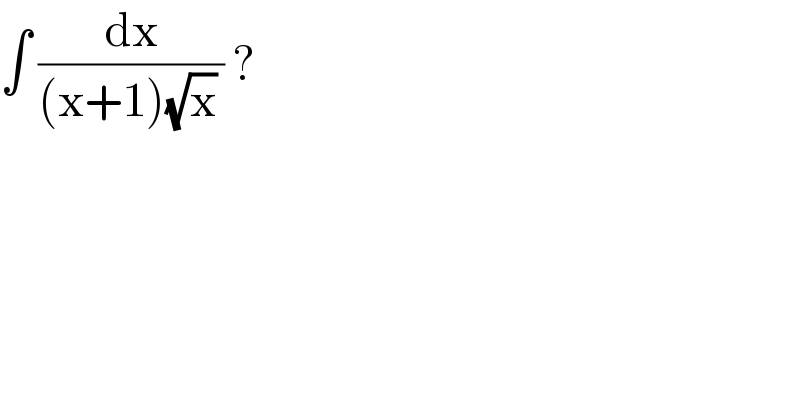
∫ (dx/((x+1)(√x) )) ?

$$\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}}\:}\:? \\ $$

Commented by TANMAY PANACEA last updated on 03/Oct/20

how to post question... here i am sharing intregation...Tanmay ∫((sinθ)/(cos3θ))+((sin3θ)/(cos9θ))+((sin9θ)/(cos27θ)) dθ

$${how}\:{to}\:{post}\:{question}... \\ $$$${here}\:{i}\:{am}\:{sharing}\:{intregation}...{Tanmay} \\ $$$$\int\frac{{sin}\theta}{{cos}\mathrm{3}\theta}+\frac{{sin}\mathrm{3}\theta}{{cos}\mathrm{9}\theta}+\frac{{sin}\mathrm{9}\theta}{{cos}\mathrm{27}\theta}\:{d}\theta \\ $$

Commented by Dwaipayan Shikari last updated on 03/Oct/20

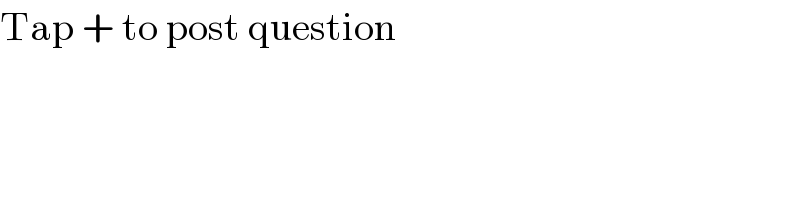
Tap + to post question

$$\mathrm{Tap}\:+\:\mathrm{to}\:\mathrm{post}\:\mathrm{question} \\ $$

Commented by TANMAY PANACEA last updated on 03/Oct/20

ok thank you sir

$${ok}\:{thank}\:{you}\:{sir} \\ $$

Commented by Dwaipayan Shikari last updated on 03/Oct/20

∫((sinθ)/(4cos^3 θ−3cosθ))+∫((sin3θ)/(4cos^3 3θ−3cos3θ))+∫((sin9θ)/(4cos^3 9θ−3cos9θ)) =∫((−dt)/(4t^3 −3t))−(1/3)∫(du/(4u^3 −3u))−(1/9)∫(dp/(4p^3 −3p)) ⇒∫((−dt)/(t(4t^2 −3)))=(1/3)∫(1/t)−((4t)/(4t^2 −3))=(1/3)log(t)−(1/6)log(4t^2 −3) And similarly −(1/3)∫(du/(4u^3 −3u))=(1/9)log(u)−(1/(18))log(4u^2 −3) −(1/3)∫(dp/(4p^3 −3p))=(1/(27))log(p)−(1/(54))log(4p^2 −3) Integral is (1/3)(log(cosθ.cos^(1/3) θ.cos^(1/9) 9θ))−(1/6)(log((4cos^2 θ−3)(4cos^2 3θ−3)^(1/3) (4cos^2 9θ−3)^(1/9) )+C

$$\int\frac{\mathrm{sin}\theta}{\mathrm{4cos}^{\mathrm{3}} \theta−\mathrm{3cos}\theta}+\int\frac{\mathrm{sin3}\theta}{\mathrm{4cos}^{\mathrm{3}} \mathrm{3}\theta−\mathrm{3cos3}\theta}+\int\frac{\mathrm{sin9}\theta}{\mathrm{4cos}^{\mathrm{3}} \mathrm{9}\theta−\mathrm{3cos9}\theta} \\ $$$$=\int\frac{−\mathrm{dt}}{\mathrm{4t}^{\mathrm{3}} −\mathrm{3t}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{du}}{\mathrm{4u}^{\mathrm{3}} −\mathrm{3u}}−\frac{\mathrm{1}}{\mathrm{9}}\int\frac{\mathrm{dp}}{\mathrm{4p}^{\mathrm{3}} −\mathrm{3p}} \\ $$$$\Rightarrow\int\frac{−\mathrm{dt}}{\mathrm{t}\left(\mathrm{4t}^{\mathrm{2}} −\mathrm{3}\right)}=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{4t}}{\mathrm{4t}^{\mathrm{2}} −\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}\left(\mathrm{t}\right)−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{log}\left(\mathrm{4t}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$$\mathrm{And}\:\mathrm{similarly} \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{du}}{\mathrm{4u}^{\mathrm{3}} −\mathrm{3u}}=\frac{\mathrm{1}}{\mathrm{9}}\mathrm{log}\left(\mathrm{u}\right)−\frac{\mathrm{1}}{\mathrm{18}}\mathrm{log}\left(\mathrm{4u}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{dp}}{\mathrm{4p}^{\mathrm{3}} −\mathrm{3p}}=\frac{\mathrm{1}}{\mathrm{27}}\mathrm{log}\left(\mathrm{p}\right)−\frac{\mathrm{1}}{\mathrm{54}}\mathrm{log}\left(\mathrm{4p}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$$\mathrm{Integral}\:\mathrm{is} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{log}\left(\mathrm{cos}\theta.\mathrm{cos}^{\frac{\mathrm{1}}{\mathrm{3}}} \theta.\mathrm{cos}^{\frac{\mathrm{1}}{\mathrm{9}}} \mathrm{9}\theta\right)\right)−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{log}\left(\left(\mathrm{4cos}^{\mathrm{2}} \theta−\mathrm{3}\right)\left(\mathrm{4cos}^{\mathrm{2}} \mathrm{3}\theta−\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{4cos}^{\mathrm{2}} \mathrm{9}\theta−\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{9}}} \right)+\mathrm{C}\right. \\ $$

Commented by Dwaipayan Shikari last updated on 03/Oct/20

Kindly don′t tell me sir. I am a student.Thanking you

$$\mathrm{Kindly}\:\mathrm{don}'\mathrm{t}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{am}\:\mathrm{a}\:\mathrm{student}.\mathrm{Thanking}\:\mathrm{you} \\ $$

Commented by mnjuly1970 last updated on 03/Oct/20

good for you nice solution peace be upon you...

$$\:\:{good}\:{for}\:\:{you}\:\:{nice}\:{solution} \\ $$$${peace}\:\:{be}\:{upon}\:{you}... \\ $$

Commented by TANMAY PANACEA last updated on 03/Oct/20

tan3θ−tanθ =((sin3θcosθ−sinθcos3θ)/(cos3θcosθ))=((2sinθcosθ)/(cos3θcosθ)) ((sinθ)/(cos3θ))=(1/2)[tan3θ−tanθ] ((sin3θ)/(cos9θ))=(1/2)[tan9θ−tan3θ] ((sin9θ)/(cos27θ))=(1/2)[tan27θ−tan9θ] add them=(1/2)[tan27θ−tanθ] so I=∫(1/2)(tan27θ−tanθ)dθ =(1/2)[((lnsec27θ)/(27))−lnsecθ]+c

$${tan}\mathrm{3}\theta−{tan}\theta \\ $$$$=\frac{{sin}\mathrm{3}\theta{cos}\theta−{sin}\theta{cos}\mathrm{3}\theta}{{cos}\mathrm{3}\theta{cos}\theta}=\frac{\mathrm{2}{sin}\theta{cos}\theta}{{cos}\mathrm{3}\theta{cos}\theta} \\ $$$$\frac{{sin}\theta}{{cos}\mathrm{3}\theta}=\frac{\mathrm{1}}{\mathrm{2}}\left[{tan}\mathrm{3}\theta−{tan}\theta\right] \\ $$$$\frac{{sin}\mathrm{3}\theta}{{cos}\mathrm{9}\theta}=\frac{\mathrm{1}}{\mathrm{2}}\left[{tan}\mathrm{9}\theta−{tan}\mathrm{3}\theta\right] \\ $$$$\frac{{sin}\mathrm{9}\theta}{{cos}\mathrm{27}\theta}=\frac{\mathrm{1}}{\mathrm{2}}\left[{tan}\mathrm{27}\theta−{tan}\mathrm{9}\theta\right] \\ $$$${add}\:{them}=\frac{\mathrm{1}}{\mathrm{2}}\left[{tan}\mathrm{27}\theta−{tan}\theta\right] \\ $$$${so}\:{I}=\int\frac{\mathrm{1}}{\mathrm{2}}\left({tan}\mathrm{27}\theta−{tan}\theta\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{lnsec}\mathrm{27}\theta}{\mathrm{27}}−{lnsec}\theta\right]+{c} \\ $$$$ \\ $$

Answered by bemath last updated on 03/Oct/20

∫ (dx/((x+1)(√x) )) ? Letting x = h^2 →dx=2h dh ∫ ((2h dh)/((h^2 +1).h)) = ∫ ((2 dh)/(h^2 +1)) = 2 tan^(−1) (h) + c = 2tan^(−1) ((√x) ) + c

$$\:\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}}\:}\:? \\ $$$$\:\mathrm{Letting}\:\mathrm{x}\:=\:\mathrm{h}^{\mathrm{2}} \:\rightarrow\mathrm{dx}=\mathrm{2h}\:\mathrm{dh} \\ $$$$\int\:\frac{\mathrm{2h}\:\mathrm{dh}}{\left(\mathrm{h}^{\mathrm{2}} +\mathrm{1}\right).\mathrm{h}}\:=\:\int\:\frac{\mathrm{2}\:\mathrm{dh}}{\mathrm{h}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{h}\right)\:+\:\mathrm{c} \\ $$$$\:=\:\mathrm{2tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\:\right)\:+\:\mathrm{c}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com