
Question and Answers Forum
Question Number 116417 by bemath last updated on 03/Oct/20
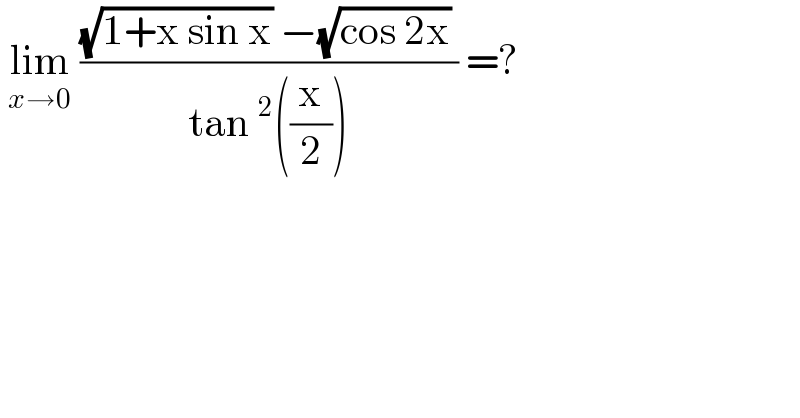
Answered by Bird last updated on 03/Oct/20

Answered by bobhans last updated on 04/Oct/20
![lim_(x→0) (((1+xsin x)−(1−2sin^2 x))/(tan^2 ((1/2)x))) ×lim_(x→0) (1/( (√(1+xsin x))+(√(cos 2x)))) = lim_(x→0) ((xsin x+2sin^2 x)/(tan^2 ((1/2)x))) × (1/2) = (1/2)×lim_(x→0) (([((x sin x)/x^2 ) +((2 sin^2 x)/x^2 )])/( [((tan^2 ((1/2)x))/x^2 )])) = (1/2)×(3/(((1/4))))= 6.](Q116424.png)
| ||
Question and Answers Forum | ||
Question Number 116417 by bemath last updated on 03/Oct/20 | ||
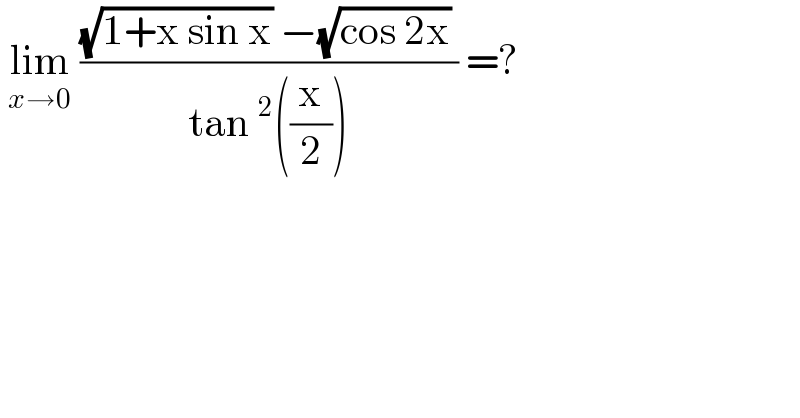 | ||
Answered by Bird last updated on 03/Oct/20 | ||
 | ||
| ||
Answered by bobhans last updated on 04/Oct/20 | ||
![lim_(x→0) (((1+xsin x)−(1−2sin^2 x))/(tan^2 ((1/2)x))) ×lim_(x→0) (1/( (√(1+xsin x))+(√(cos 2x)))) = lim_(x→0) ((xsin x+2sin^2 x)/(tan^2 ((1/2)x))) × (1/2) = (1/2)×lim_(x→0) (([((x sin x)/x^2 ) +((2 sin^2 x)/x^2 )])/( [((tan^2 ((1/2)x))/x^2 )])) = (1/2)×(3/(((1/4))))= 6.](Q116424.png) | ||
| ||