Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 116436 by mnjuly1970 last updated on 04/Oct/20

$. . . a d v a n c e d c a l c u l u s . . .$ $e v a l u a t e ::$ $I = \int_{0}^{\infty} (\frac{s i n (x) . s i n (2 x)}{x}) d x = ? ? ?$ $. . . m . n . 1970 . . .$
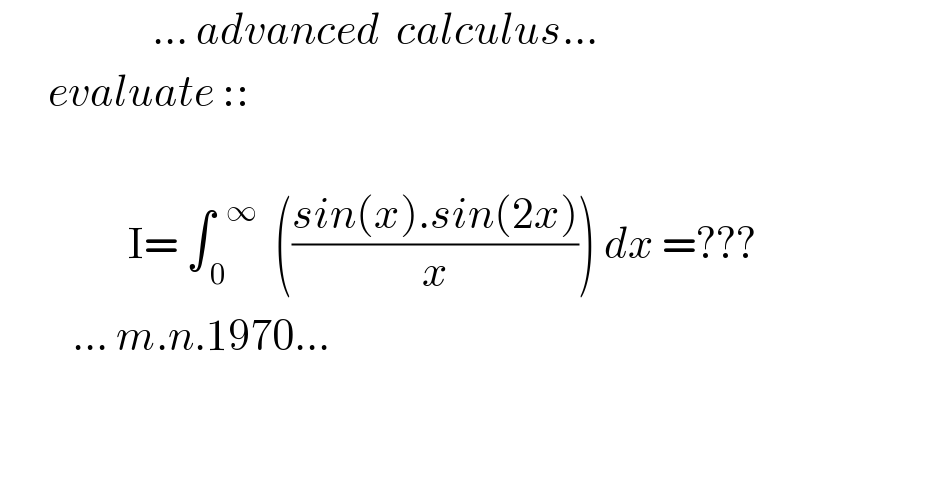
Commented by Bird last updated on 04/Oct/20

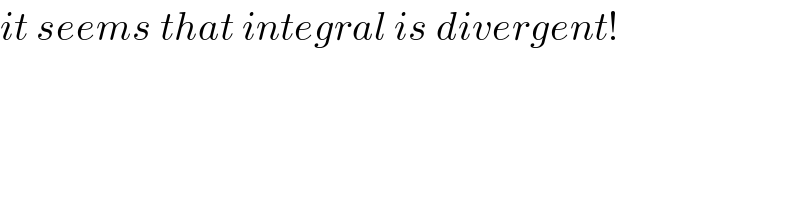
$i t s e e m s t h a t i n t e g r a l i s d i v e r g e n t!$
Commented by mathdave last updated on 04/Oct/20

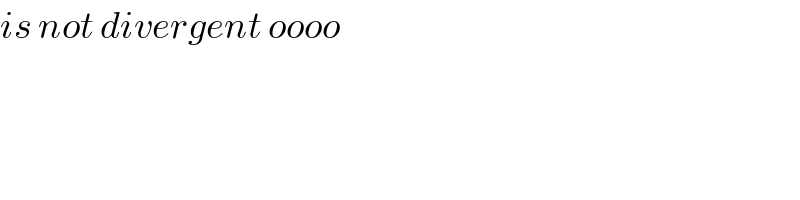
$i s n o t d i v e r g e n t o o o o$
	Answered by mnjuly1970 last updated on 04/Oct/20


	Answered by Bird last updated on 05/Oct/20
	$let take a try we have sinx.sin(2x)=cos((π/2)−x)cos((π/2)−2x) =(1/2){cos(π−3x)+cos(x)} =(1/2){cosx−cos(3x)} ⇒ I =(1/2)∫_0 ^∞ ((cosx−cos(3x))/x)dx I =∫_0 ^∞ ((1−cos(3x))/(2x))dx−∫_0 ^∞ ((1−cosx)/(2x))dx =(1/2)(u−v) let f(a) =∫_0 ^∞ ((1−cosx)/x)e^(−ax) dx with a>0 f^′ (a) =−∫_0 ^∞ (1−cosx)e^(−ax) dx =∫_0 ^∞ e^(−ax) cosxdx−∫_0 ^∞ e^(−ax) dx ∫_0 ^∞ e^(−ax) dx=[−(1/a)e^(−ax) ]_0 ^∞ =(1/a) ∫_0 ^∞ e^(−ax+ix) dx =∫_0 ^∞ e^((−a+i)x) dx =[(1/(−a+i)) e^((−a+i)x) ]_0 ^∞ =−(1/(−a+i))=(1/(a−i)) =((a+i)/(a^2 +1)) ⇒∫_0 ^∞ e^(−ax) cosxdx =Re(...) =(a/(1+a^2 )) ⇒ f^′ (a) =(a/(1+a^2 ))−(1/a) ⇒ f(a) =(1/2)ln(1+a^2 )−lna +c =ln(((√(1+a^2 ))/a)) +c lim_(a→+∞) f(a) =0 =c ⇒ f(a) =ln(((√(1+a^2 ))/a)) ∫_0 ^∞ ((1−cosx)/x)dx =lim_(a→0) f(a) dont exist also ∫_0 ^∞ ((1−cos(3x))/x)dxdont exist but we see ∫_0 ^∞ ((1−cos(3x))/x)dx=_(3x=t) 3∫_0 ^∞ ((1−cost)/t)(dt/3) =∫_0 ^∞ ((1−cosx)/x)dx I =0$
	$l e t t a k e a t r y w e h a v e$ $s i n x . s i n (2 x) = c o s (\frac{π}{2} - x) c o s (\frac{π}{2} - 2 x)$ $= \frac{1}{2} {c o s (π - 3 x) + c o s (x)}$ $= \frac{1}{2} {c o s x - c o s (3 x)} \Rightarrow$ $I = \frac{1}{2} \int_{0}^{\infty} \frac{c o s x - c o s (3 x)}{x} d x$ $I = \int_{0}^{\infty} \frac{1 - c o s (3 x)}{2 x} d x - \int_{0}^{\infty} \frac{1 - c o s x}{2 x} d x$ $= \frac{1}{2} (u - v)$ $l e t f (a) = \int_{0}^{\infty} \frac{1 - c o s x}{x} e^{- a x} d x w i t h a > 0$ $f^{^{'}} (a) = - \int_{0}^{\infty} (1 - c o s x) e^{- a x} d x$ $= \int_{0}^{\infty} e^{- a x} c o s x d x - \int_{0}^{\infty} e^{- a x} d x$ $\int_{0}^{\infty} e^{- a x} d x = {[- \frac{1}{a} e^{- a x}]}_{0}^{\infty}$ $= \frac{1}{a}$ $\int_{0}^{\infty} e^{- a x + i x} d x = \int_{0}^{\infty} e^{(- a + i) x} d x$ $= {[\frac{1}{- a + i} e^{(- a + i) x}]}_{0}^{\infty} = - \frac{1}{- a + i} = \frac{1}{a - i}$ $= \frac{a + i}{a^{2} + 1} \Rightarrow \int_{0}^{\infty} e^{- a x} c o s x d x$ $= R e (. . .) = \frac{a}{1 + a^{2}} \Rightarrow$ $f^{^{'}} (a) = \frac{a}{1 + a^{2}} - \frac{1}{a} \Rightarrow$ $f (a) = \frac{1}{2} l n (1 + a^{2}) - l n a + c$ $= l n (\frac{\sqrt{1 + a^{2}}}{a}) + c$ ${l i m}_{a \to + \infty} f (a) = 0 = c \Rightarrow$ $f (a) = l n (\frac{\sqrt{1 + a^{2}}}{a})$ $\int_{0}^{\infty} \frac{1 - c o s x}{x} d x = {l i m}_{a \to 0} f (a)$ $d o n t e x i s t a l s o \int_{0}^{\infty} \frac{1 - c o s (3 x)}{x} d x d o n t$ $e x i s t b u t w e s e e$ $\int_{0}^{\infty} \frac{1 - c o s (3 x)}{x} d x =_{3 x = t} 3 \int_{0}^{\infty} \frac{1 - c o s t}{t} \frac{d t}{3}$ $= \int_{0}^{\infty} \frac{1 - c o s x}{x} d x I = 0$
	Commented by Bird last updated on 05/Oct/20

	$u = v \Rightarrow I = 0$
	Commented by mnjuly1970 last updated on 05/Oct/20
	$solution: method 1 : I =L [((sin(x).sin(2x)/x)]_(s=0) = L [sin(x) sin(2x)]=(1/2) L [cos(x−2x) −cos(x+2x)] =(1/2) L [cos(x)]− (1/2) L [cos(3x)] =(1/2)∗ (s/(s^2 +1)) −(1/2)∗ (s/(s^2 +9)) I = {(1/2)∫_s ^( ∞) (u/(u^2 +1)) du − (1/2) ∫_s ^( ∞) (u/(u^2 +9))du}_(s=0) ={(1/4) [ln (((u^2 +1)/(u^2 +9)))]_( u=s) ^( u=∞) = (1/4) ln((1/9))−(1/4) ln(((s^2 +1)/(s^2 +9)) )}_(s=0) =[((−1)/2) ln(3) − (1/4)ln(((s^2 +1)/(s^2 +9)))]_( s=0) = thank you your effort and work is admirable ...$
	$s o l u t i o n :$ $m e t h o d 1 : I = L {[\frac{s i n (x) . s i n (2 x}{x}]}_{s = 0}$ $= L [s i n (x) s i n (2 x)] = \frac{1}{2} L [c o s (x - 2 x) - c o s (x + 2 x)]$ $= \frac{1}{2} L [c o s (x)] - \frac{1}{2} L [c o s (3 x)]$ $= \frac{1}{2} * \frac{s}{s^{2} + 1} - \frac{1}{2} * \frac{s}{s^{2} + 9}$ $I = {\frac{1}{2} \int_{s}^{\infty} \frac{u}{u^{2} + 1} d u - \frac{1}{2} \int_{s}^{\infty} \frac{u}{u^{2} + 9} d u}_{s = 0}$ $= {\frac{1}{4} {[l n (\frac{u^{2} + 1}{u^{2} + 9})]}_{u = s}^{u = \infty} = \frac{1}{4} l n (\frac{1}{9}) - \frac{1}{4} l n (\frac{s^{2} + 1}{s^{2} + 9})}_{s = 0}$ $= {[\frac{- 1}{2} l n (3) - \frac{1}{4} l n (\frac{s^{2} + 1}{s^{2} + 9})]}_{s = 0}$ $=$ $t h a n k y o u y o u r e f f o r t a n d$ $w o r k i s a d m i r a b l e . . .$
	Answered by mathdave last updated on 05/Oct/20

	$s o l u t i o n$ $w e k n o w \sin x \sin 2 x = \frac{1}{2} (\cos x - \cos 3 x)$ $l e t I = \int_{0}^{\infty} \frac{\sin x \sin 2 x}{x} d x = \frac{1}{2} \int_{0}^{\infty} (\frac{\cos x - \cos 3 x}{x}) d x$ $f r o m m a z i d e n t i t y$ $\int_{0}^{\infty} f (t) G (t) d t = \int^{\infty} f (s) g (s) d s b u t n o t e$ $L (f (t)) = f (s) a n d L^{- 1} (G (t)) = g (s)$ $I = \frac{1}{2} \int_{0}^{\infty} L (\cos x - \cos 3 x) L^{- 1} {(\frac{1}{x})}_{s = x} d s b u t l^{- 1} (\frac{1}{x}) = 1$ $I = \frac{1}{2} \int_{0}^{\infty} (\frac{s}{s^{2} + 1} - \frac{s}{s^{2} + 9}) d s \frac{1}{2} \int_{0}^{\infty} \frac{2 s}{2 (s^{2} + 1)} d s - \frac{1}{2} \int_{0}^{\infty} \frac{2 s}{2 (s^{2} + 9)} d s = \frac{1}{4} \ln {(\frac{s^{2} + 1}{s^{2} + 9})}_{0}^{\infty}$ $I = \frac{1}{4} (0 - \ln (\frac{1}{9})) = \frac{\ln (3)}{2}$ $∵ \int_{0}^{\infty} \frac{\sin x \sin 2 x}{x} d x = \frac{\ln (3)}{2}$ $b y m a t h d a v e (05 / 10 / 2020)$
	Commented by mnjuly1970 last updated on 06/Oct/20

	$t h a n k y o u$ $v e r y n i c e a s a l w a y s . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum