
Question and Answers Forum
Question Number 116437 by ZiYangLee last updated on 04/Oct/20
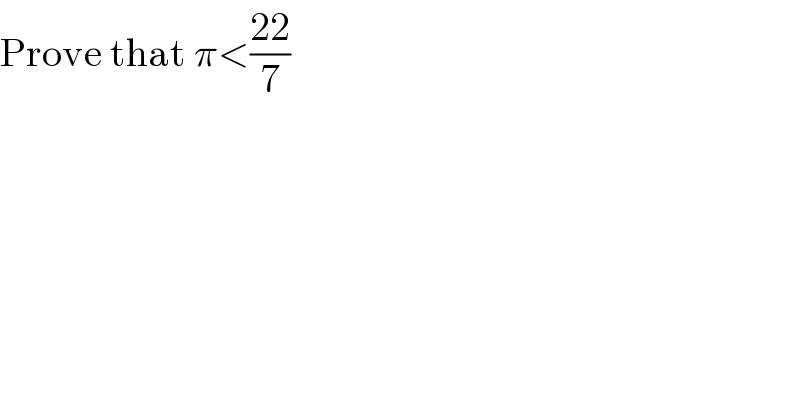
Answered by floor(10²Eta[1]) last updated on 04/Oct/20
![let′s look at the integral and solve it: I(x)=∫_0 ^1 ((x^4 (1−x)^4 )/(1+x^2 ))dx =∫_0 ^1 ((x^8 −4x^7 +6x^6 −4x^5 +x^4 )/(1+x^2 ))dx =∫_0 ^1 (x^6 −4x^5 +5x^4 −4x^2 +4−(4/(1+x^2 )))dx =[(x^7 /7)−((2x^6 )/3)+x^5 −((4x^3 )/3)+4x−4tan^(−1) (x)]_0 ^1 =((22)/7)−π and since I(x)>0 so ((22)/7)−π>0⇒π<((22)/7)](Q116438.png)
Commented byZiYangLee last updated on 04/Oct/20

Answered by MJS_new last updated on 04/Oct/20
![the area of a regular polygon with n sides and an incircle of radius 1 is A_n =n(√((1−cos ((2π)/n))/(1+cos ((2π)/n)))) lim_(n→∞) A_n =π [ _(approximates the circle)^(obvious because the polygon) ] if ((22)/7)<π ⇒ A_n =((22)/7) has no solution ∈R ⇔ if A_n =((22)/7) ⇒ ((22)/7)>π A_n =((22)/7) ⇒ n≈90.4298 ⇒ ((22)/7)>π](Q116477.png)
| ||
Question and Answers Forum | ||
Question Number 116437 by ZiYangLee last updated on 04/Oct/20 | ||
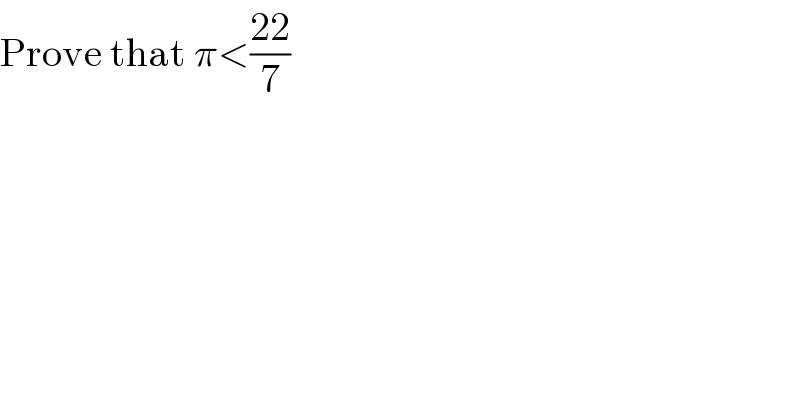 | ||
Answered by floor(10²Eta[1]) last updated on 04/Oct/20 | ||
![let′s look at the integral and solve it: I(x)=∫_0 ^1 ((x^4 (1−x)^4 )/(1+x^2 ))dx =∫_0 ^1 ((x^8 −4x^7 +6x^6 −4x^5 +x^4 )/(1+x^2 ))dx =∫_0 ^1 (x^6 −4x^5 +5x^4 −4x^2 +4−(4/(1+x^2 )))dx =[(x^7 /7)−((2x^6 )/3)+x^5 −((4x^3 )/3)+4x−4tan^(−1) (x)]_0 ^1 =((22)/7)−π and since I(x)>0 so ((22)/7)−π>0⇒π<((22)/7)](Q116438.png) | ||
| ||
Commented byZiYangLee last updated on 04/Oct/20 | ||
 | ||
Answered by MJS_new last updated on 04/Oct/20 | ||
![the area of a regular polygon with n sides and an incircle of radius 1 is A_n =n(√((1−cos ((2π)/n))/(1+cos ((2π)/n)))) lim_(n→∞) A_n =π [ _(approximates the circle)^(obvious because the polygon) ] if ((22)/7)<π ⇒ A_n =((22)/7) has no solution ∈R ⇔ if A_n =((22)/7) ⇒ ((22)/7)>π A_n =((22)/7) ⇒ n≈90.4298 ⇒ ((22)/7)>π](Q116477.png) | ||
| ||