Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 116451 by bemath last updated on 04/Oct/20

$$\underset{\mathrm{n}\to \mathrm{\infty }}{\lim }\frac{\sqrt[\mathrm{n}]{(\mathrm{n}+1)(\mathrm{n}+2)(\mathrm{n}+3)...(\mathrm{n}+\mathrm{n})}}{\mathrm{n}}=?$$

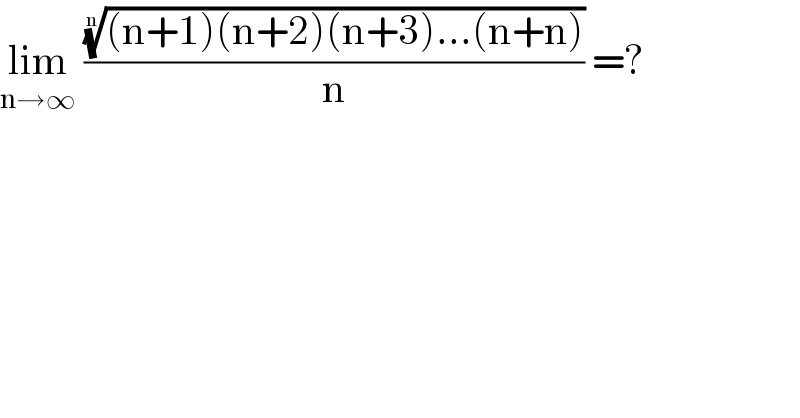
Commented by Olaf last updated on 04/Oct/20

$$\mathbf{Sorry}{\mathbf{I}}^{\prime }\mathbf{m}\mathbf{wrong}!$$$$\mathrm{I}\mathbf{calculated}\mathbf{another}\mathbf{expression}!$$$$!??!{\mathbf{I}}^{\prime }\mathbf{m}\mathbf{tired}!$$

Answered by Olaf last updated on 04/Oct/20

$$u_n={}^n\sqrt{\frac{\underset{k=1}{\prod ^n}(n+k)}{n}}$$$$v_n=\ln u_n$$$$v_n=\frac{1}{n}(\ln \underset{k=1}{\prod ^n}(n+k)-\ln n)$$$$v_n=\frac{1}{n}(\ln \underset{k=1}{\prod ^n}n(1+\frac{k}{n})-\ln n)$$$$v_n=\frac{1}{n}(\ln n^n\underset{k=1}{\prod ^n}(1+\frac{k}{n})-\ln n)$$$$v_n=\frac{1}{n}(n\ln n+\ln \underset{k=1}{\prod ^n}(1+\frac{k}{n})-\ln n)$$$$v_n=\frac{1}{n}(n\ln n+\underset{k=1}{\sum ^n}\ln (1+\frac{k}{n})-\ln n)$$$$\ln (1+\frac{k}{n})\underset{\mathrm{\infty }}{\sim }\frac{k}{n}$$$$v_n\underset{\mathrm{\infty }}{\sim }\frac{1}{n}(n\ln n+\underset{k=1}{\sum ^n}\frac{k}{n}-\ln n)$$$$v_n\underset{\mathrm{\infty }}{\sim }\frac{1}{n}(n\ln n+\frac{1}{n}.\frac{n(n+1)}{2}-\ln n)$$$$v_n\underset{\mathrm{\infty }}{\sim }\ln n+\frac{n+1}{2n}-\frac{\ln n}{n}=+\mathrm{\infty }+\frac{1}{2}-0$$$$\underset{n\to \mathrm{\infty }}{\lim }{v}_n=+\mathrm{\infty }$$$$\underset{n\to \mathrm{\infty }}{\lim }{u}_n=\underset{n\to \mathrm{\infty }}{\lim }{e}^{v_n}=+\mathrm{\infty }$$$$$$$$$$

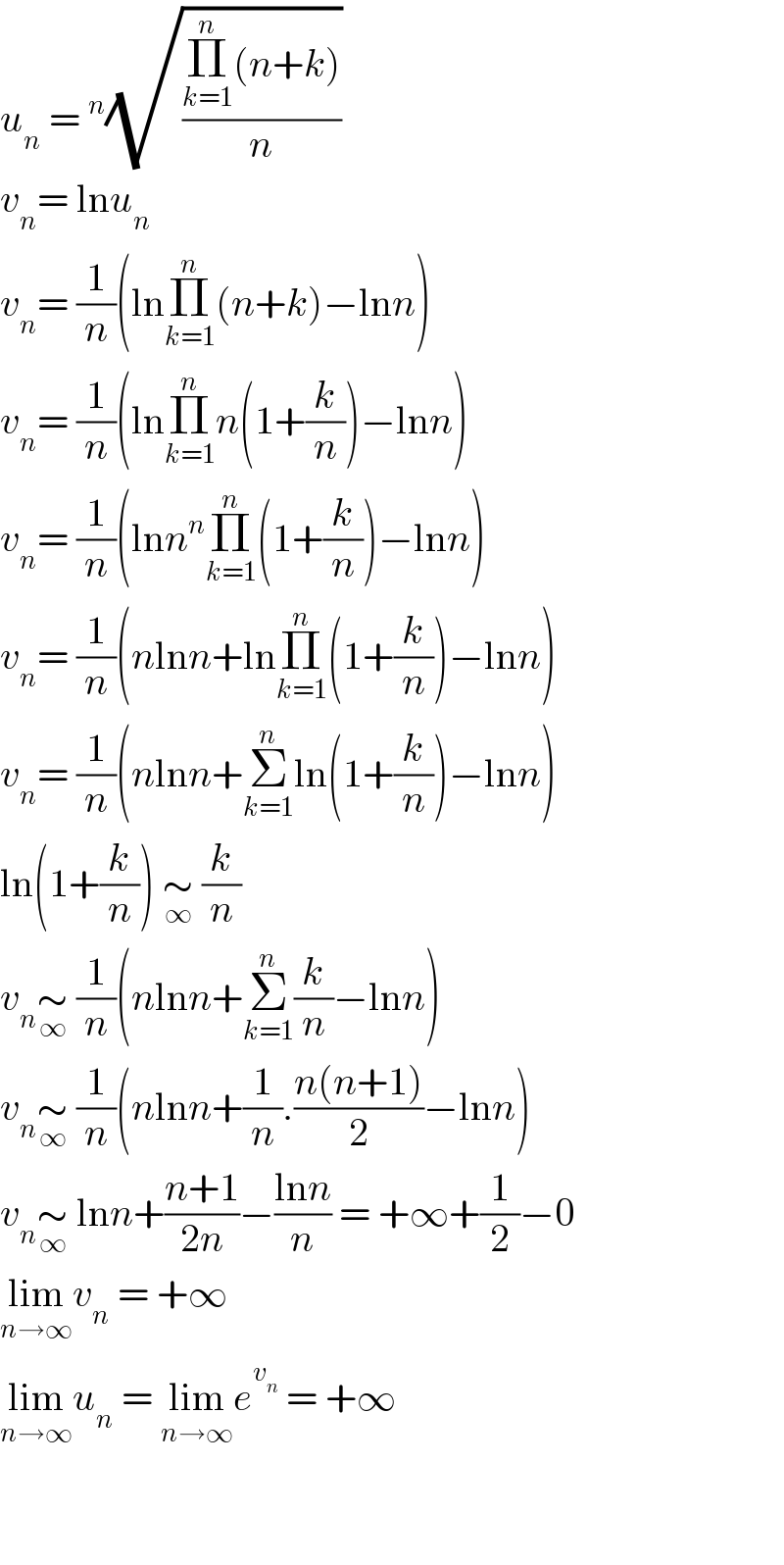
Commented by bemath last updated on 04/Oct/20

$$\mathrm{thank}\mathrm{you}\mathrm{sir}$$

Answered by Dwaipayan Shikari last updated on 04/Oct/20

$$\underset{\mathrm{n}\to \mathrm{\infty }}{\lim }\sqrt[\mathrm{n}]{(1+\frac{1}{\mathrm{n}})(1+\frac{2}{\mathrm{n}})(1+\frac{3}{\mathrm{n}})..}=\mathrm{y}$$$$\underset{\mathrm{n}\to \mathrm{\infty }}{\lim }\frac{1}{\mathrm{n}}\underset{\mathrm{k}=1}{\sum ^{\mathrm{n}}}\log (1+\frac{\mathrm{k}}{\mathrm{n}})=\mathrm{logy}$$$${\int }_0^1\log (1+\mathrm{x})\mathrm{dx}=\mathrm{logy}$$$${\left[\mathrm{xlog}(1+\mathrm{x})\right]}_0^1-{\int }_0^1\frac{\mathrm{x}}{1+\mathrm{x}}=\mathrm{logy}$$$$\log \left(2\right)-1+{\left[\log (1+\mathrm{x})\right]}_0^1=\mathrm{logy}$$$$2\log \left(2\right)-1=\mathrm{logy}$$$$\mathrm{y}=\frac{4}{\mathrm{e}}$$

Answered by mnjuly1970 last updated on 04/Oct/20

$$solution$$$$l={lim}_{n\to \mathrm{\infty }}\frac{\sqrt[n]{(n+1)(n+2)...(n+n)}}{n}$$$$l={lim}_{n\to \mathrm{\infty }}\sqrt[n]{(1+\frac{1}{n})(1+\frac{2}{n})...(1+\frac{n}{n})}$$$$log\left(l\right)={lim}_{n\to \mathrm{\infty }}\frac{1}{n}\underset{k=}{\sum ^n}log(1+\frac{k}{n})$$$$={\int }_0^{1}log(1+x)dx={\int }_1^{2}log\left(t\right)dt$$$$={[tlog\left(t\right)-t]}_1^2=2log\left(2\right)-2+1$$$$=log\left(4\right)-log\left(e\right)=log\left(\frac{4}{e}\right)$$$$\therefore l:=\frac{4}{e}✓✓$$$$...m.n.1970...$$$$$$$$$$

Commented by bemath last updated on 04/Oct/20

$$\mathrm{yes}...\mathrm{thank}\mathrm{you}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com