find u_n =∫_0 ^∞ ((sin^n x)/x)dx (n≥1)


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 116533 by Bird last updated on 04/Oct/20

$f i n d u_{n} = \int_{0}^{\infty} \frac{{s i n}^{n} x}{x} d x (n ⩾ 1)$
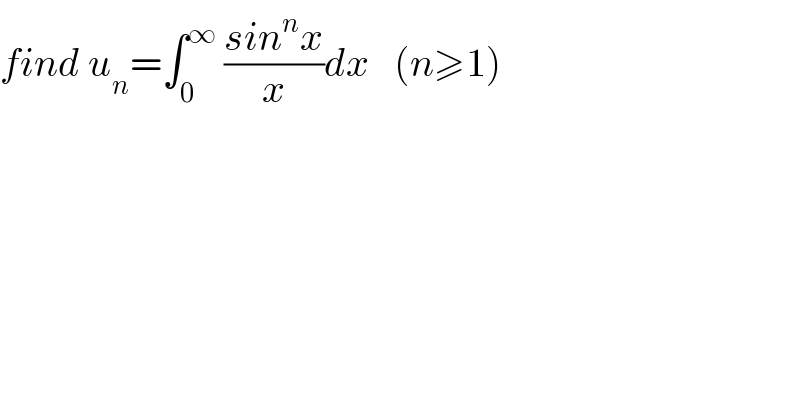
	Answered by Olaf last updated on 04/Oct/20

	$1 st case : n is odd$ $\sin^{n} x = \frac{1}{2^{n - 1}} {(- 1)}^{\frac{n - 1}{2}} \underset{k = 0}{\sum^{\frac{n - 1}{2}}} {(- 1)}^{k} C_{n}^{k} \sin [(n - 2 k) x]$ $u_{n} = \frac{1}{2^{n - 1}} {(- 1)}^{\frac{n - 1}{2}} \underset{k = 0}{\sum^{\frac{n - 1}{2}}} {(- 1)}^{k} C_{n}^{k} \int_{0}^{\infty} \frac{\sin [(n - 2 k) x]}{x} d x$ $t = (n - 2 k) x$ $u_{n} = \frac{1}{2^{n - 1}} {(- 1)}^{\frac{n - 1}{2}} \underset{k = 0}{\sum^{\frac{n - 1}{2}}} {(- 1)}^{k} C_{n}^{k} \int_{0}^{\infty} \frac{\sin t}{t} d t$ $With \int_{0}^{\infty} \frac{\sin t}{t} d t = \frac{π}{2} (Dirichlet)$ $u_{n} = \frac{π}{2^{n}} {(- 1)}^{\frac{n - 1}{2}} \underset{k = 0}{\sum^{\frac{n - 1}{2}}} {(- 1)}^{k} C_{n}^{k}$ $2 nd case : n is even$ $\sin^{n} x = \frac{1}{2^{n - 1}} {(- 1)}^{\frac{n}{2}} (\underset{k = 0}{\sum^{\frac{n - 2}{2}}} {(- 1)}^{k} C_{n}^{k} \cos [(n - 2 k) x] + \frac{1}{2} {(- 1)}^{\frac{n}{2}} C_{n}^{\frac{n}{2}})$ $u_{n} = \frac{1}{2^{n - 1}} {(- 1)}^{\frac{n}{2}} (\underset{k = 0}{\sum^{\frac{n - 2}{2}}} {(- 1)}^{k} C_{n}^{k} \int_{0}^{\infty} \frac{\cos [(n - 2 k) x]}{x} d x + \frac{1}{2} {(- 1)}^{\frac{n}{2}} C_{n}^{\frac{n}{2}} \int_{0}^{\infty} \frac{d x}{x})$ $u_{n} = \frac{1}{2^{n - 1}} {(- 1)}^{\frac{n}{2}} (\underset{k = 0}{\sum^{\frac{n - 2}{2}}} {(- 1)}^{k} C_{n}^{k} \int_{0}^{\infty} \frac{\cos t}{t} d t + \frac{1}{2} {(- 1)}^{\frac{n}{2}} C_{n}^{\frac{n}{2}} \int_{0}^{\infty} \frac{d t}{t})$ $? ? ? ?$
	Commented by mathmax by abdo last updated on 04/Oct/20

	$thank you sir$
	Commented by maths mind last updated on 04/Oct/20

	$\int_{0}^{\infty} \frac{{s i n}^{2 n} (x)}{x} d x d o n t C o n v e r g e$ $\underset{k = 0}{\sum^{\infty}} \int_{2 k π}^{2 (k + 1) π} \frac{{s i n}^{2 n} (x)}{x} d x ⩾ \underset{k = 0}{\sum^{\infty}} \int_{2 k π + \frac{π}{4}}^{2 k π + \frac{π}{2}} \frac{{s i n}^{2 n} (x)}{x} d x$ $⩾ \sum_{k ⩾ 0} \frac{{(\frac{\sqrt{2}}{2})}^{2 n}}{2 (k + 1) π} \to \infty$
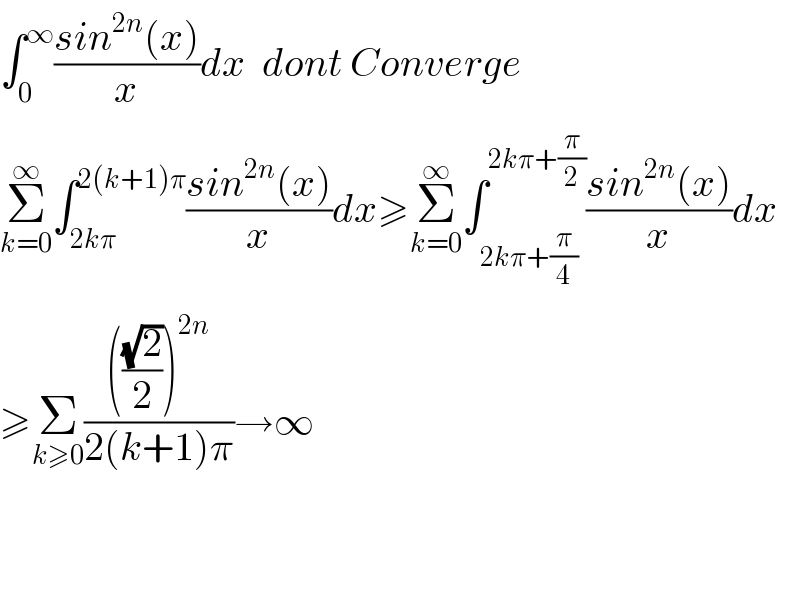
	Answered by mathmax by abdo last updated on 04/Oct/20
	$we have sinx =((e^(ix) −e^(−ix) )/(2i)) ⇒sin^n x =(1/((2i)^n ))(e^(ix) −e^(−ix) )^n =(1/((2i)^n ))Σ_(k=0) ^n C_(n ) ^k (e^(ix) )^k (−e^(−ix) )^(n−k) =(1/((2i)^n )) Σ_(k=0) ^n C_n ^k e^(ikx) (−1)^(n−k) e^(−i(n−k)x) =(1/((2i)^n )) Σ_(k.0) ^n (−1)^k C_n ^k e^(ikx−(n−k)ix) =(1/((2i)^n )) Σ_(k=0) ^n (−1)^k C_n ^k e^(i(2k−n)x) =(1/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k {cos(2k−n)x +isin(2k−n)x} ⇒ u_n =(1/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k ∫_0 ^∞ ((cos(2k−n)x)/x)dx +(i/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k ∫_0 ^∞ ((sin(2k−n)x)/x)dx ∫_0 ^∞ ((sin(2k−n)x)/x)dx =_(2k−n)x=t) (2k−n) ∫_0 ^∞ ((sint)/t)(dt/(2k−n)) =(π/2) ⇒ u_n =(1/((2i)^n )) Σ_(k=0) ^n (−1)^k C_n ^k ∫_0 ^∞ ((cos(2k−n)x)/x)dx+(π/2)(i/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k ∫_0 ^∞ ((cos(2k−n)x)/x)dx =_((2k−n)x=t) (2k−n) ∫_0 ^∞ ((cost)/t)(dt/(2k−n)) =∫_0 ^∞ ((cost)/t) dt =Re(∫_0 ^∞ (e^(it) /t)dt) but ∫_0 ^∞ (e^(it) /t) dt =∫_0 ^∞ (e^(−(−it)) /t)dt =_(−it =u) ∫_0 ^(i∞) (e^(−u) /(u/(−i)))idu =∫_0 ^(i∞) u^(−1) e^(−u) du ....be continued....$
	$we have sinx = \frac{e^{ix} - e^{- ix}}{2 i} \Rightarrow \sin^{n} x = \frac{1}{{(2 i)}^{n}} {(e^{ix} - e^{- ix})}^{n}$ $= \frac{1}{{(2 i)}^{n}} \sum_{k = 0}^{n} C_{n}^{k} {(e^{ix})}^{k} {(- e^{- ix})}^{n - k}$ $= \frac{1}{{(2 i)}^{n}} \sum_{k = 0}^{n} C_{n}^{k} e^{ikx} {(- 1)}^{n - k} e^{- i (n - k) x}$ $= \frac{1}{{(2 i)}^{n}} \sum_{k . 0}^{n} {(- 1)}^{k} C_{n}^{k} e^{ikx - (n - k) ix}$ $= \frac{1}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} e^{i (2 k - n) x}$ $= \frac{1}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} {\cos (2 k - n) x + isin (2 k - n) x} \Rightarrow$ $u_{n} = \frac{1}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} \int_{0}^{\infty} \frac{\cos (2 k - n) x}{x} dx + \frac{i}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} \int_{0}^{\infty} \frac{\sin (2 k - n) x}{x} dx$ $\int_{0}^{\infty} \frac{\sin (2 k - n) x}{x} dx =_{2 k - n) x = t} (2 k - n) \int_{0}^{\infty} \frac{sint}{t} \frac{dt}{2 k - n}$ $= \frac{π}{2} \Rightarrow$ $u_{n} = \frac{1}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} \int_{0}^{\infty} \frac{\cos (2 k - n) x}{x} dx + \frac{π}{2} \frac{i}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k}$ $\int_{0}^{\infty} \frac{\cos (2 k - n) x}{x} dx =_{(2 k - n) x = t} (2 k - n) \int_{0}^{\infty} \frac{cost}{t} \frac{dt}{2 k - n}$ $= \int_{0}^{\infty} \frac{cost}{t} dt = Re (\int_{0}^{\infty} \frac{e^{it}}{t} dt) but$ $\int_{0}^{\infty} \frac{e^{it}}{t} dt = \int_{0}^{\infty} \frac{e^{- (- it)}}{t} dt =_{- it = u} \int_{0}^{i \infty} \frac{e^{- u}}{\frac{u}{- i}} idu = \int_{0}^{i \infty} u^{- 1} e^{- u} du$ $. . . . be continued . . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum