Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 116557 by Bird last updated on 04/Oct/20

$$calculate{\int }_0^{\mathrm{\infty }}\frac{ln(1+x(1+t^2)}{1+t^2}dt$$ $$withx>0$$ $$2)findthevalueof{\int }_0^{\mathrm{\infty }}\frac{ln(2+t^2)}{1+t^2}dt$$ $$and{\int }_0^{\mathrm{\infty }}\frac{ln(3+2t^2)}{1+t^2}dt$$

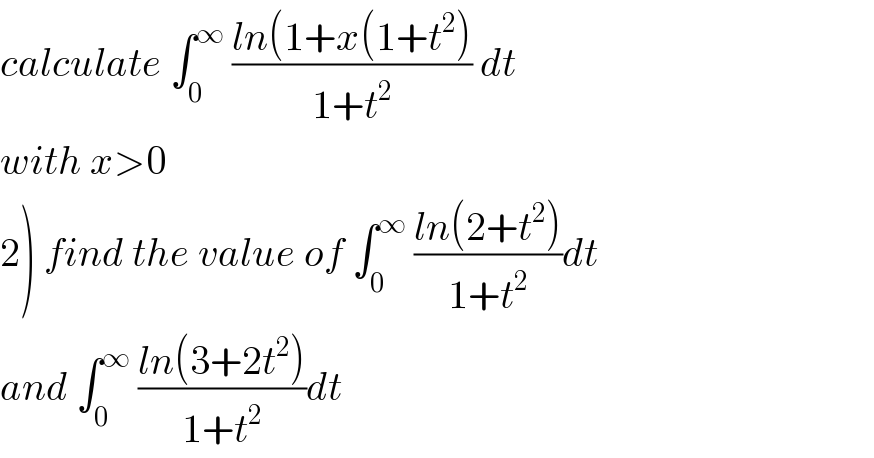
Answered by mindispower last updated on 05/Oct/20

$$f\left(x\right)={\int }_0^{\mathrm{\infty }}\frac{ln(1+x(1+t^2))}{1+t^2}dt$$ $$f^{\prime }\left(x\right)={\int }_0^{\mathrm{\infty }}\frac{dt}{1+x(1+t^2)}$$ $$={\int }_0^{\mathrm{\infty }}\frac{dt}{(1+x)(1+{\left(\frac{t}{\sqrt{1+x}}\right)}^2)}$$ $$=\frac{1}{\sqrt{1+x}}{\left[{\tan }^{-1}\left(\frac{t}{\sqrt{1+x}}\right)\right]}_0^{\mathrm{\infty }}$$ $$=\frac{\pi }{2\sqrt{1+x}}$$ $$f\left(0\right)=0$$ $$f\left(x\right)={\int }_0^x\frac{\pi }{2\sqrt{1+x}}=\pi \sqrt{1+x}$$ $${\int }_0^{\mathrm{\infty }}\frac{ln(2+t^2)}{1+t^2}dt=f\left(1\right)=\pi \sqrt{2}$$ $${\int }_0^{\mathrm{\infty }}\frac{ln(3+2t^2)}{1+t^2}dt=f\left(2\right)=\pi \sqrt{3}$$ $$$$

Commented bymathmax by abdo last updated on 05/Oct/20

$$\mathrm{thanks}\mathrm{sir}$$

Commented bymathmax by abdo last updated on 05/Oct/20

$$(1+\mathrm{x})(1+{\left(\frac{\mathrm{t}}{\sqrt{1+\mathrm{x}}}\right)}^2)=(1+\mathrm{x})\{1+\frac{{\mathrm{t}}^2}{1+\mathrm{x}}\}=1+\mathrm{x}+{\mathrm{t}}^2\ne 1+\mathrm{x}(1+{\mathrm{t}}^2)!$$ $$$$

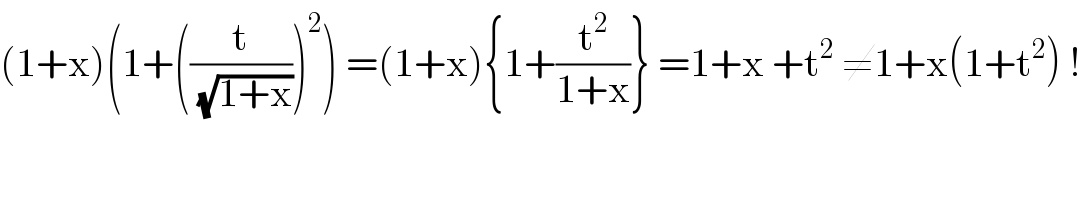
Answered by mathmax by abdo last updated on 05/Oct/20

$$1)\mathrm{let}\mathrm{f}\left(\mathrm{x}\right)={\int }_0^{\mathrm{\infty }}\frac{\ln (1+\mathrm{x}(1+{\mathrm{t}}^2))}{1+{\mathrm{t}}^2}\mathrm{dt}\mathrm{we}\mathrm{have}{\mathrm{f}}^{{}^{\prime }}\left(\mathrm{x}\right)={\int }_0^{\mathrm{\infty }}\frac{\mathrm{dt}}{1+\mathrm{x}(1+{\mathrm{t}}^2)}$$ $$={\int }_0^{\mathrm{\infty }}\frac{\mathrm{dt}}{{\mathrm{xt}}^2+\mathrm{x}+1}=\frac{1}{\mathrm{x}}{\int }_0^{\mathrm{\infty }}\frac{\mathrm{dt}}{{\mathrm{t}}^2+\frac{\mathrm{x}+1}{\mathrm{x}}}{=}_{\mathrm{t}=\sqrt{\frac{\mathrm{x}+1}{\mathrm{x}}}\mathrm{u}}\frac{1}{\mathrm{x}}.\frac{\mathrm{x}}{\mathrm{x}+1}{\int }_0^{\mathrm{\infty }}\frac{1}{{\mathrm{u}}^2+1}\frac{\sqrt{\mathrm{x}+1}}{\sqrt{\mathrm{x}}}\mathrm{du}$$ $$=\frac{1}{\sqrt{\mathrm{x}}\sqrt{\mathrm{x}+1}}\Rightarrow \mathrm{f}\left(\mathrm{x}\right)=\int \frac{\mathrm{dx}}{\sqrt{\mathrm{x}}\sqrt{\mathrm{x}+1}}+\mathrm{c}$$ $${=}_{\sqrt{\mathrm{x}}=\mathrm{z}}\int \frac{2\mathrm{zdz}}{\mathrm{z}\sqrt{{\mathrm{z}}^2+1}}+\mathrm{c}=2\int \frac{\mathrm{dz}}{\sqrt{{\mathrm{z}}^2+1}}+\mathrm{c}$$ $$=2\ln (\mathrm{z}+\sqrt{1+{\mathrm{z}}^2})+\mathrm{c}=2\ln (\sqrt{\mathrm{x}}+\sqrt{1+\mathrm{x}})+\mathrm{c}$$ $$\mathrm{f}\left(0\right)=0=2\ln \left(1\right)+\mathrm{c}=\mathrm{c}\Rightarrow \mathrm{f}\left(\mathrm{x}\right)=2\ln (\sqrt{\mathrm{x}}+\sqrt{1+\mathrm{x}})$$ $$2){\int }_0^{\mathrm{\infty }}\frac{\ln (2+{\mathrm{t}}^2)}{1+{\mathrm{t}}^2}\mathrm{dt}=\mathrm{f}\left(1\right)=2\ln (1+\sqrt{2})$$ $${\int }_0^{\mathrm{\infty }}\frac{\ln (3+{2\mathrm{t}}^2)}{1+{\mathrm{t}}^2}\mathrm{dt}=\mathrm{f}\left(2\right)=2\ln (\sqrt{2}+\sqrt{3})$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com