
Question and Answers Forum
Question Number 116603 by ZiYangLee last updated on 05/Oct/20
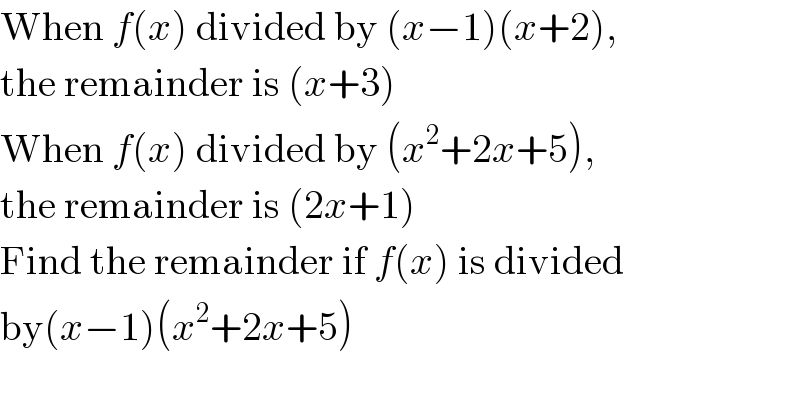
Answered by 1549442205PVT last updated on 06/Oct/20
![From the hypothesis we have: f(x)=p(x)(x−1)(x+2)+x+3(1) f(x)=q(x)(x^2 +2x+5)+2x+1 ⇔f(x)=q(x)([x−(−1+2i)][x−(−1−2i)] +2x+1(2) We have x^2 +2x+5=0⇔x=−1±2i (2)⇒f(−1+2i)=2(−1+2i)+1=−1+4i f(−1−2i)=2(−1−2i)+1=−1−4i We need find r(x)=ax^2 +bx+c so that f(x)=h(x)(x−1)(x^2 +2x+5)+r(x)(3) From(1)(2)we get { ((f(1)=4,f(−2)=1)),((f(−1+2i)=−1+4i,f(−1−2i)=−1−4i)) :} Put into (3) we get i)4=f(1)=a+b+c ii)−1+4i=a(−1+2i)^2 +b(−1+2i)+c ⇔−1+4i=−5a−4ai−b+2bi+c ⇔(−5a−b+c+1)+(2b−4a−4)i=0 ⇔ { ((−5a−b+c+1=0)),((2b−4a−4=0)) :} iii)−1−4i=a(−1−2i)^2 +b(−1−2i)+c ⇔−1−4i=−5a+4ai−b−2bi+c ⇔−5a−b+c+1+(4a−2b+4)i=0 ⇔ { ((−5a−b+c+1=0)),((4a−2b+4=0)) :} We obtain the system of three eqns { ((a+b+c=4(4))),((−5a−b+c+1=0(5))),((4a−2b+4=0(6))) :} Substract (4) from (5)we get 6a+2b−5=0 ,adding this equation to (6) we get 10a−1=0⇒a=1/10 ⇒b=11/10,c=28/10.Therefore we get r(x)=0.1x^2 +1.1x+2.8](Q116749.png)
| ||
Question and Answers Forum | ||
Question Number 116603 by ZiYangLee last updated on 05/Oct/20 | ||
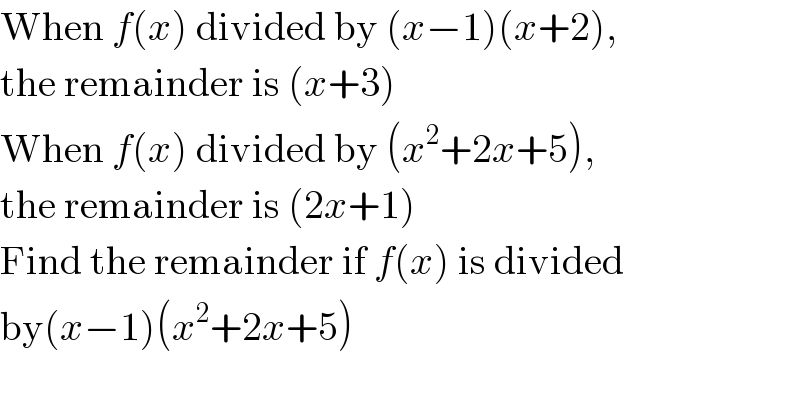 | ||
Answered by 1549442205PVT last updated on 06/Oct/20 | ||
![From the hypothesis we have: f(x)=p(x)(x−1)(x+2)+x+3(1) f(x)=q(x)(x^2 +2x+5)+2x+1 ⇔f(x)=q(x)([x−(−1+2i)][x−(−1−2i)] +2x+1(2) We have x^2 +2x+5=0⇔x=−1±2i (2)⇒f(−1+2i)=2(−1+2i)+1=−1+4i f(−1−2i)=2(−1−2i)+1=−1−4i We need find r(x)=ax^2 +bx+c so that f(x)=h(x)(x−1)(x^2 +2x+5)+r(x)(3) From(1)(2)we get { ((f(1)=4,f(−2)=1)),((f(−1+2i)=−1+4i,f(−1−2i)=−1−4i)) :} Put into (3) we get i)4=f(1)=a+b+c ii)−1+4i=a(−1+2i)^2 +b(−1+2i)+c ⇔−1+4i=−5a−4ai−b+2bi+c ⇔(−5a−b+c+1)+(2b−4a−4)i=0 ⇔ { ((−5a−b+c+1=0)),((2b−4a−4=0)) :} iii)−1−4i=a(−1−2i)^2 +b(−1−2i)+c ⇔−1−4i=−5a+4ai−b−2bi+c ⇔−5a−b+c+1+(4a−2b+4)i=0 ⇔ { ((−5a−b+c+1=0)),((4a−2b+4=0)) :} We obtain the system of three eqns { ((a+b+c=4(4))),((−5a−b+c+1=0(5))),((4a−2b+4=0(6))) :} Substract (4) from (5)we get 6a+2b−5=0 ,adding this equation to (6) we get 10a−1=0⇒a=1/10 ⇒b=11/10,c=28/10.Therefore we get r(x)=0.1x^2 +1.1x+2.8](Q116749.png) | ||
| ||