Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 116614 by bemath last updated on 05/Oct/20
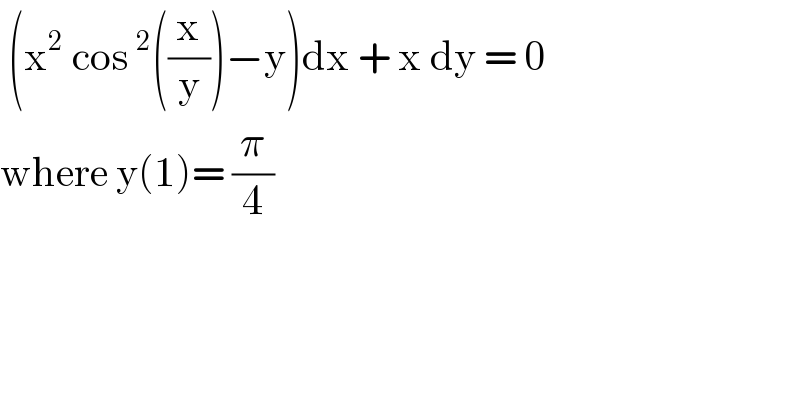
Commented by TANMAY PANACEA last updated on 05/Oct/20
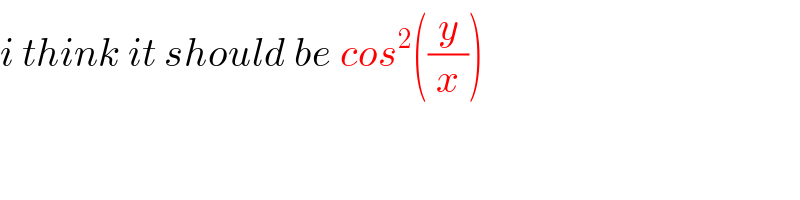
Commented by bobhans last updated on 05/Oct/20
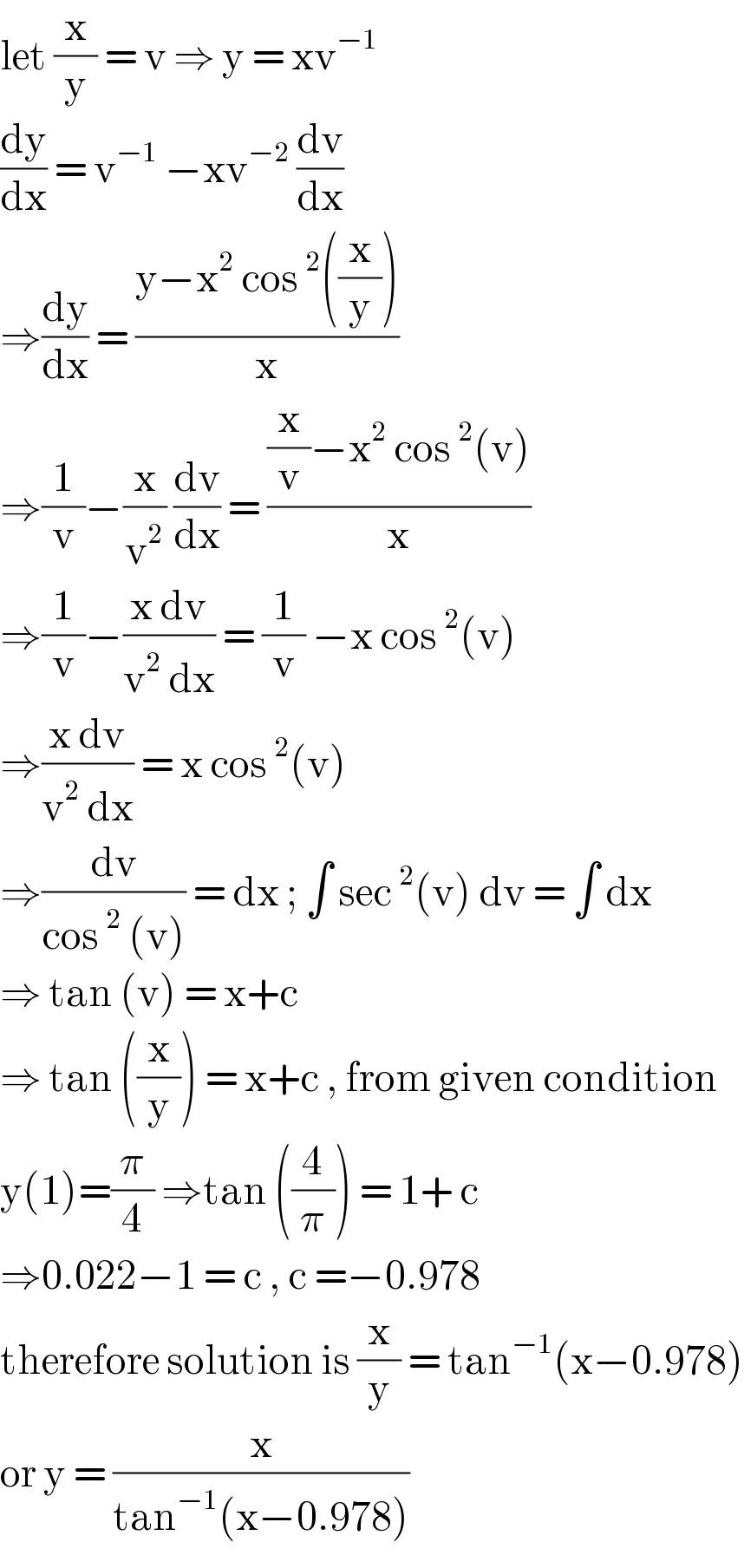
Commented by bemath last updated on 05/Oct/20
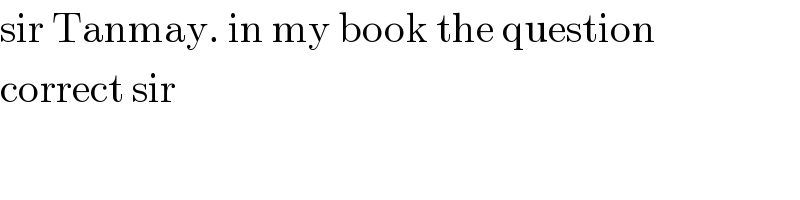
Answered by TANMAY PANACEA last updated on 05/Oct/20
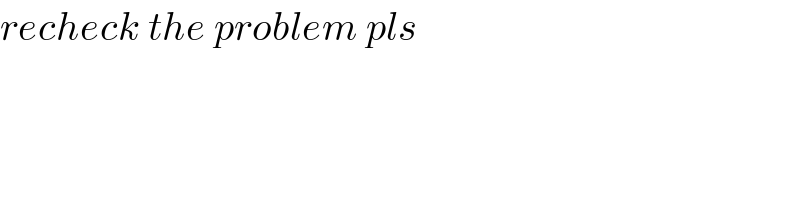
Answered by TANMAY PANACEA last updated on 05/Oct/20