
Question and Answers Forum
Question Number 116658 by zakirullah last updated on 05/Oct/20

Commented by Rasheed.Sindhi last updated on 08/Oct/20

Commented by zakirullah last updated on 08/Oct/20
Answered by mr W last updated on 05/Oct/20

Commented by zakirullah last updated on 05/Oct/20

Commented by zakirullah last updated on 05/Oct/20
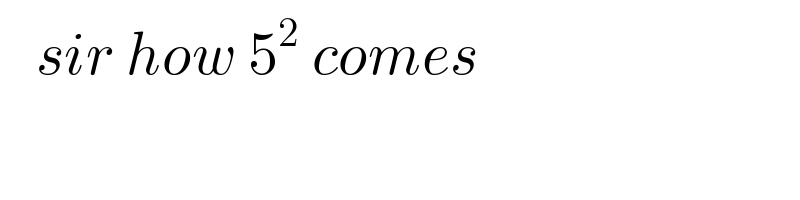
Commented by JDamian last updated on 05/Oct/20
it is on purpose. Otherwise the number wouldn't be a perfect squared. In fact, all the primes of the number must be present as an even power.
Answered by $@y@m last updated on 05/Oct/20
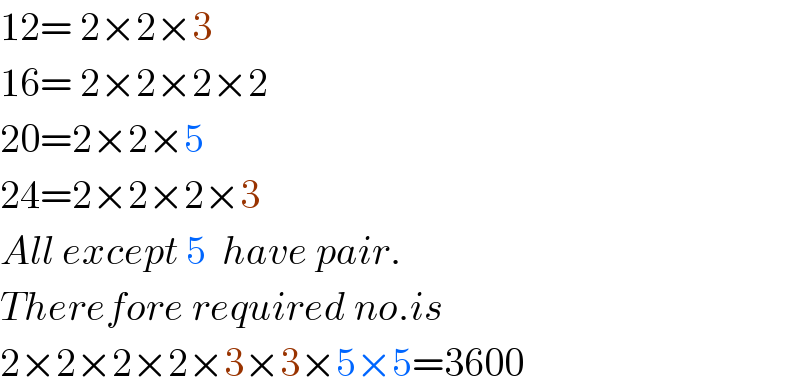
Commented by zakirullah last updated on 05/Oct/20

Commented by zakirullah last updated on 05/Oct/20

