
Question and Answers Forum
Question Number 116667 by mnjuly1970 last updated on 05/Oct/20
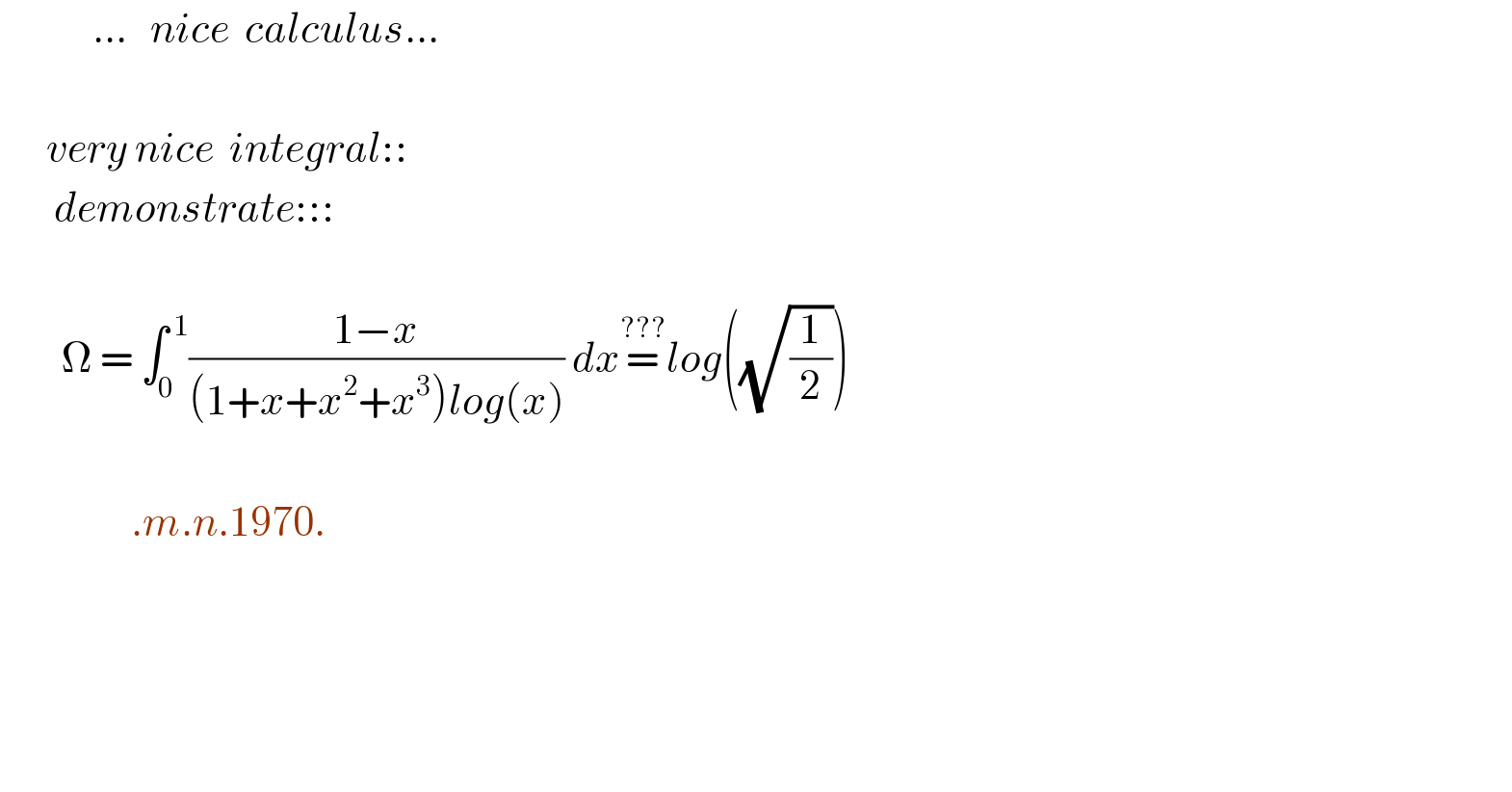
Answered by maths mind last updated on 06/Oct/20
![Hello after many tries Ω=∫_0 ^1 ((1−x)/((1+x+x^2 +x^3 ))).(dx/(log(x))) let f(a)=∫_0 ^1 ((1−x)/((1+x+x^2 +x^3 ))).(x^a /(log(x)))dx,a∈[0,1] Ω=f(0) f(a)=∫_0 ^1 (((1−x)^2 )/(1−x^4 ))..(x^a /(log(x)))dx f′(a)=∫_0 ^1 (((1−x)^2 )/((1−x^4 ))).∂_a x^a .(dx/(log(x)))=∫_0 ^1 (((x^2 −2x+1))/(1−x^4 )).x^a dx x^4 =t⇒dx=(t^(−(3/4)) /4)dt f′(a)=∫_0 ^1 ((t^(2/4) −2t^(1/4) +1)/(1−t))t^(a/4) .t^(−(3/4)) (dt/4) =−∫_0 ^1 ((1−t^((a/4)−(1/4)) )/(1−t))dt+2∫((1−t^((a/4)−(2/4)) )/(1−t))dt−∫((1−t^((a/4)−(3/4)) )/(1−t))dt we Have one of definition of Digamma Ψ(s+1)=−γ+∫_0 ^1 ((1−x^s )/(1−x))dx =(lnΓ(s+1))′ 4f′(a)=−Ψ(((a+3)/4))+2Ψ(((a+2)/4))−Ψ(((a+1)/4)) 4f(a)=−4lnΓ(((a+3)/4))−4lnΓ(((a+1)/4))+8lnΓ(((a+2)/4))+c lim_(a→∞) f(a)=0⇒c=0 f(0)=Ω 4f(0)=4Ω=−4lnΓ((3/4))−4lnΓ((1/4))+8lnΓ((1/2)) =−4ln(((Γ((1/4))Γ((3/4)))/(Γ^2 ((1/2))))):Γ((1/4))Γ(1−(1/4))=(π/(sin((π/4))))=π(√2) Γ((1/2))=(√π)⇒4Ω=−4ln(((π(√2))/(((√π))^2 )))=−4ln((√2))=4ln((√(1/2))) Ω=ln((√(1/2))) ∫_0 ^1 ((1−x)/(1+x+x^2 +x^3 )).(dx/(log(x)))=ln((√(1/2)))](Q116794.png)
Commented by maths mind last updated on 06/Oct/20
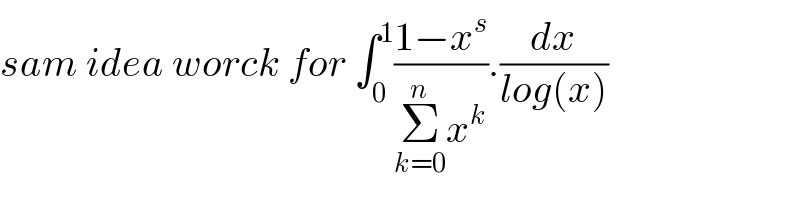
Commented by mnjuly1970 last updated on 07/Oct/20
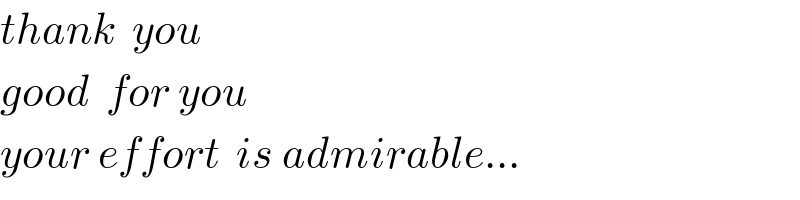
| ||
Question and Answers Forum | ||
Question Number 116667 by mnjuly1970 last updated on 05/Oct/20 | ||
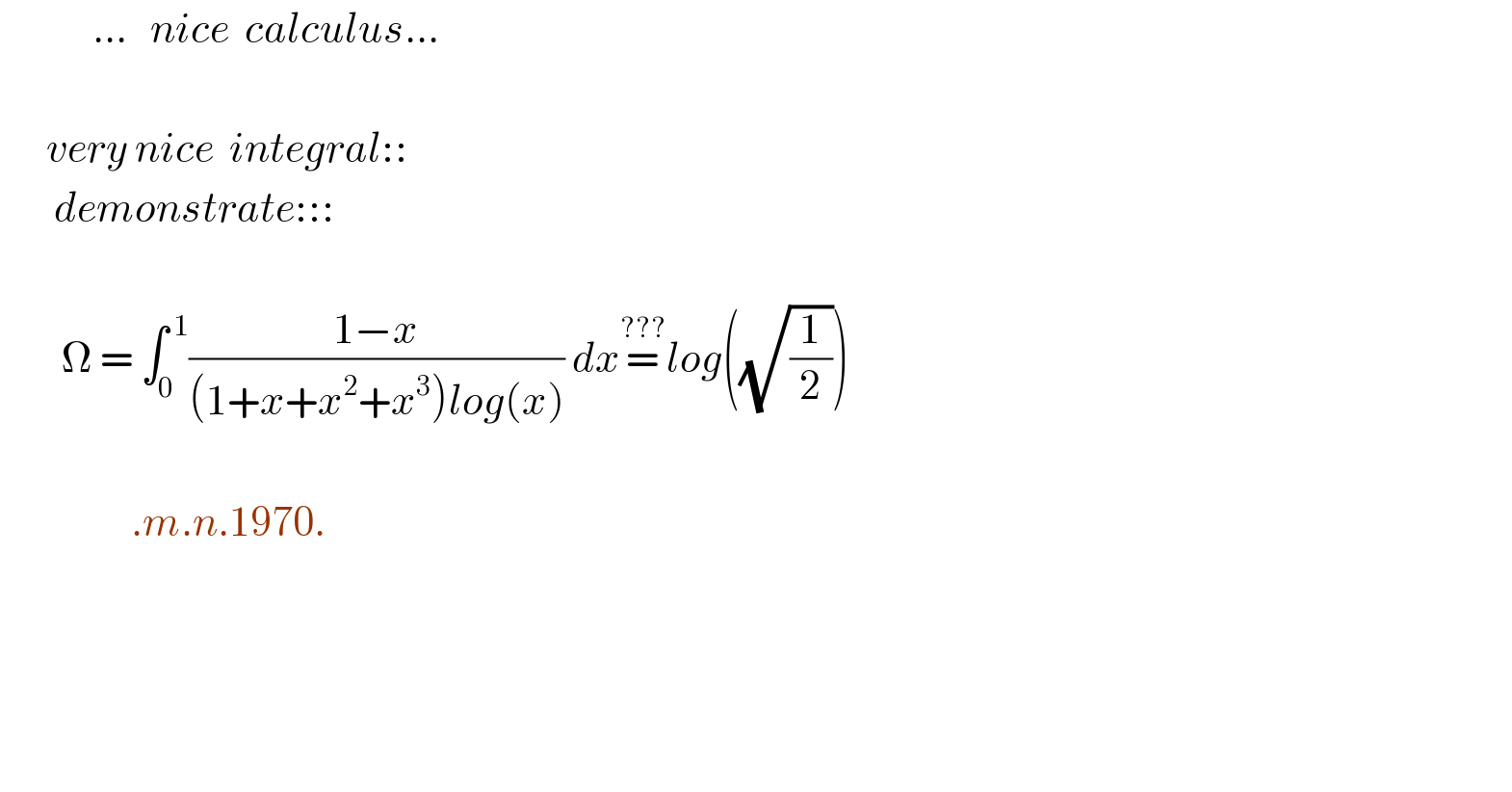 | ||
Answered by maths mind last updated on 06/Oct/20 | ||
![Hello after many tries Ω=∫_0 ^1 ((1−x)/((1+x+x^2 +x^3 ))).(dx/(log(x))) let f(a)=∫_0 ^1 ((1−x)/((1+x+x^2 +x^3 ))).(x^a /(log(x)))dx,a∈[0,1] Ω=f(0) f(a)=∫_0 ^1 (((1−x)^2 )/(1−x^4 ))..(x^a /(log(x)))dx f′(a)=∫_0 ^1 (((1−x)^2 )/((1−x^4 ))).∂_a x^a .(dx/(log(x)))=∫_0 ^1 (((x^2 −2x+1))/(1−x^4 )).x^a dx x^4 =t⇒dx=(t^(−(3/4)) /4)dt f′(a)=∫_0 ^1 ((t^(2/4) −2t^(1/4) +1)/(1−t))t^(a/4) .t^(−(3/4)) (dt/4) =−∫_0 ^1 ((1−t^((a/4)−(1/4)) )/(1−t))dt+2∫((1−t^((a/4)−(2/4)) )/(1−t))dt−∫((1−t^((a/4)−(3/4)) )/(1−t))dt we Have one of definition of Digamma Ψ(s+1)=−γ+∫_0 ^1 ((1−x^s )/(1−x))dx =(lnΓ(s+1))′ 4f′(a)=−Ψ(((a+3)/4))+2Ψ(((a+2)/4))−Ψ(((a+1)/4)) 4f(a)=−4lnΓ(((a+3)/4))−4lnΓ(((a+1)/4))+8lnΓ(((a+2)/4))+c lim_(a→∞) f(a)=0⇒c=0 f(0)=Ω 4f(0)=4Ω=−4lnΓ((3/4))−4lnΓ((1/4))+8lnΓ((1/2)) =−4ln(((Γ((1/4))Γ((3/4)))/(Γ^2 ((1/2))))):Γ((1/4))Γ(1−(1/4))=(π/(sin((π/4))))=π(√2) Γ((1/2))=(√π)⇒4Ω=−4ln(((π(√2))/(((√π))^2 )))=−4ln((√2))=4ln((√(1/2))) Ω=ln((√(1/2))) ∫_0 ^1 ((1−x)/(1+x+x^2 +x^3 )).(dx/(log(x)))=ln((√(1/2)))](Q116794.png) | ||
| ||
Commented by maths mind last updated on 06/Oct/20 | ||
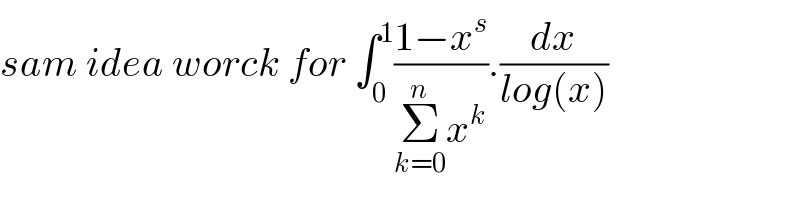 | ||
Commented by mnjuly1970 last updated on 07/Oct/20 | ||
 | ||