Question Number 116672 by mnjuly1970 last updated on 05/Oct/20
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\:\:\:{nice}\:\:{calculus}\:... \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{prove}\:\:{that}\:: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\pi}{\mathrm{4}}\:\:−\mathscr{A}{rctan}\left({x}\right)\right)\frac{{dx}}{\mathrm{1}−{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{G}}{\mathrm{2}}\:\:\checkmark\:\:\:\: \\ $$$$\:\:\:\:\:\:\: \\ $$$$\mathrm{G}\:{is}\:\:\:{catalan}\:\:{constant}\:... \\ $$$$\:\:\:\:\:\:\:\mathscr{M}.\mathscr{N}.\mathrm{1970} \\ $$$$ \\ $$$$ \\ $$$$\:\:\: \\ $$
Answered by mnjuly1970 last updated on 05/Oct/20
![solution: I = ∫_0 ^( 1) (Arctan(1) −Arctan(x ))dx I=∫_0 ^( 1) Arctan(((1−x)/(1+x)))(dx/(1−x^2 )) I =^(( ((1−x)/(1+x))=t )) −2∫_1 ^( 0) Arctan(t)(dt/((1+t)^2 [1−(((1−t)/(1+t)))^2 ])) I = 2∫_0 ^( 1) ((Arctan(t))/(4t)) dt = (1/2) ∫_0 ^( 1) ((Arctan(t))/t)dt I =(1/2) ∫_0 ^( 1) Σ_(n=0) ^∞ (((−1)^n t^(2n) )/((2n+1))) dt=(1/2) Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 )) I := (G/2) ✓✓ ...m.n.july.1970...](Q116673.png)
$$\:\:\:\:\:{solution}: \\ $$$$\:\:\:\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\mathscr{A}{rctan}\left(\mathrm{1}\right)\:−\mathscr{A}{rctan}\left({x}\:\right)\right){dx} \\ $$$$\:\:\:\mathrm{I}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathscr{A}{rctan}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)\frac{{dx}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\:\:\:\mathrm{I}\:\overset{\left(\:\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}={t}\:\right)} {=}\:−\mathrm{2}\int_{\mathrm{1}} ^{\:\mathrm{0}} \:\mathscr{A}{rctan}\left({t}\right)\frac{{dt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} \left[\mathrm{1}−\left(\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\right)^{\mathrm{2}} \right]}\: \\ $$$$\:\:\mathrm{I}\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathscr{A}{rctan}\left({t}\right)}{\mathrm{4}{t}}\:{dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathscr{A}{rctan}\left({t}\right)}{{t}}{dt} \\ $$$$\:\:\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {t}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)}\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{I}\::=\:\frac{\mathrm{G}}{\mathrm{2}}\:\:\checkmark\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{m}.{n}.{july}.\mathrm{1970}... \\ $$$$ \\ $$
Answered by Bird last updated on 06/Oct/20
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\pi}{\mathrm{4}}−{arctanx}\right)\frac{{dx}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${we}\:{have}\:{tan}\left(\:\frac{\pi}{\mathrm{4}}−{arctsnx}\right)\:= \\ $$$$\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\:\Rightarrow\frac{\pi}{\mathrm{4}}−{arctanx}\:={arctan}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{arctan}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$${ch}\:\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}={t}\:{give}\:\mathrm{1}−{x}\:={t}\:+{tx}\:\Rightarrow \\ $$$$\mathrm{1}−{t}\:=\left(\mathrm{1}+{t}\right){x}\:\Rightarrow{x}\:=\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\:\Rightarrow \\ $$$$\frac{{dx}}{{dt}}\:=\frac{−\left(\mathrm{1}+{t}\right)−\left(\mathrm{1}−{t}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }=\frac{−\mathrm{2}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{arctan}\left({t}\right)}{\mathrm{1}−\frac{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }}×\frac{−\mathrm{2}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{arctant}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} −\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{arctan}\left({t}\right)}{\mathrm{1}+\mathrm{2}{t}\:+{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{2}{t}\:−{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{arctant}}{{t}}{dt}\:{we}\:{have} \\ $$$$\left({arctant}\right)^{'} \:=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{2}{n}} \\ $$$$\Rightarrow\:{arctan}\left({t}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\Rightarrow\frac{{arctant}}{{t}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}{t}^{\mathrm{2}{n}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{arctant}}{{t}}{dt}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }={K} \\ $$$$\Rightarrow{I}\:=\frac{{K}}{\mathrm{2}}\:\:\left({katalan}\:{constante}\right) \\ $$$$ \\ $$
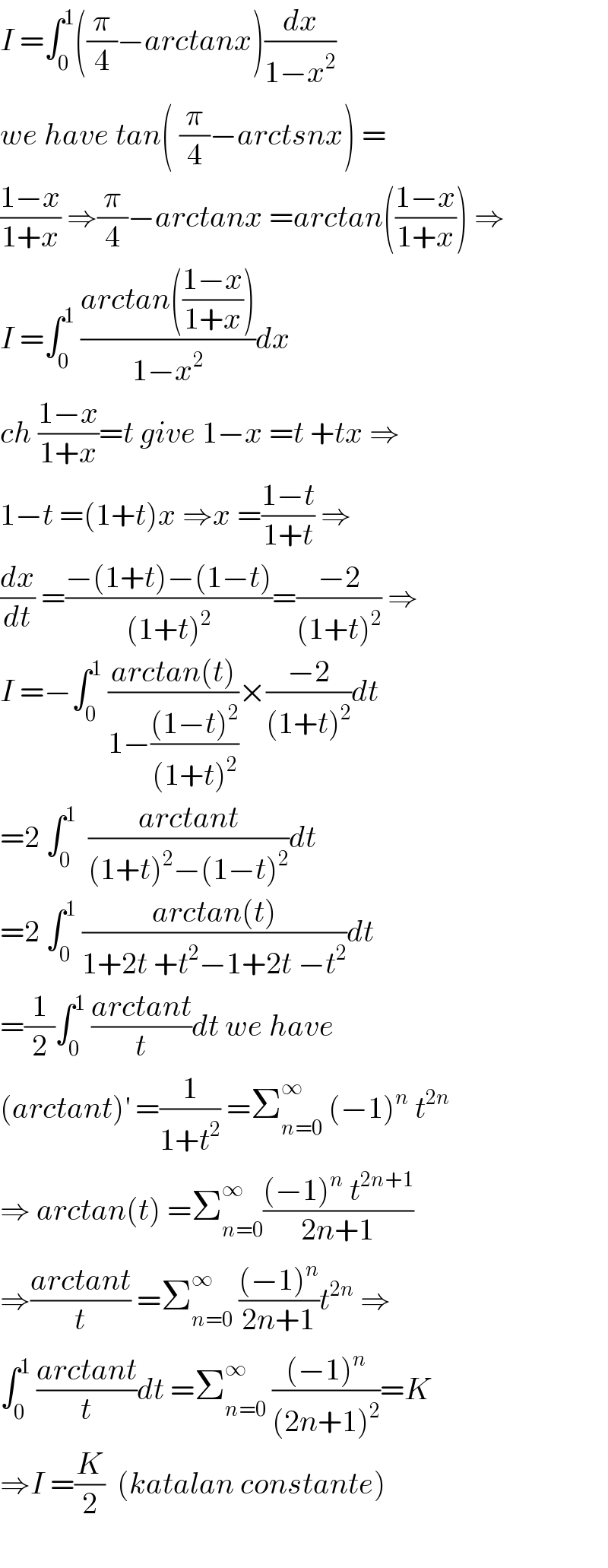
Commented by mnjuly1970 last updated on 06/Oct/20
$${thank}\:\:{you}\:\:{very}\:{much}... \\ $$
Commented by Bird last updated on 07/Oct/20
$${you}\:{are}\:{welcome} \\ $$