
Question and Answers Forum
Question Number 116710 by ravisoni505 last updated on 06/Oct/20

Answered by maths mind last updated on 06/Oct/20
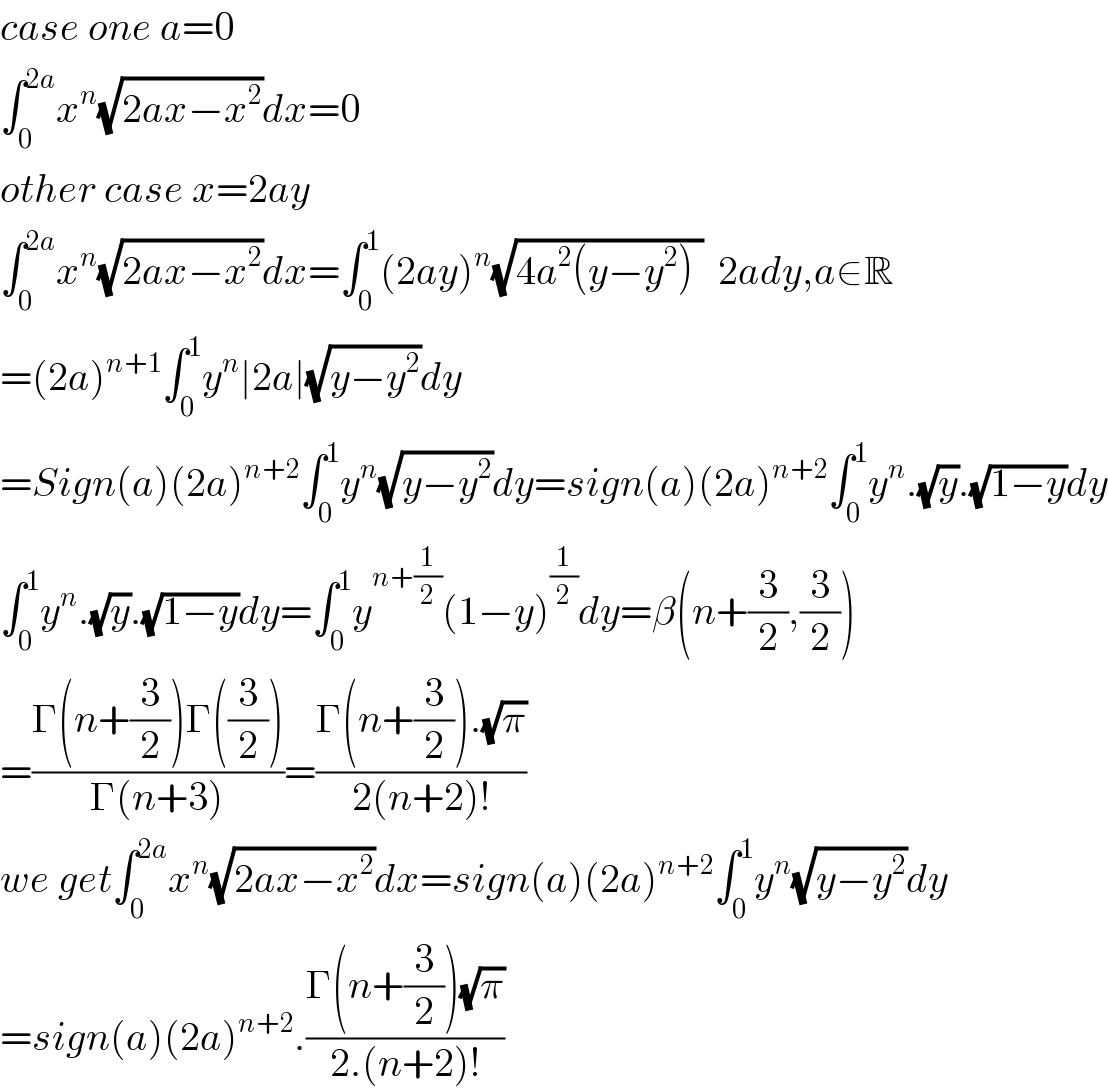
Answered by mathmax by abdo last updated on 06/Oct/20
![I_n =∫_0 ^(2a) x^n (√(2ax−x^2 )) dx ⇒ I_n =∫_0 ^(2a) x^n (√x)(√(2a−x))dx =_((√x)=t) ∫_0 ^(√(2a)) t^(2n) t(√(2a−t^2 ))2t dt =2 ∫_0 ^(√(2a)) t^(2n+2) (√(((√(2a)))^2 −t^2 ))dt =_(t=(√(2a))sinθ) 2 ∫_0 ^(arcsin((√(2a)))) sin^(2n+2) θ(√(2a))cost (√(2a))cost dt =4a ∫_0 ^(arcsin((√(2a)))) sin^(2n+2) cos^2 t dt =4a ∫_0 ^(arcsin((√(2a)))) sin^(2n+2) t(1−sin^2 t)dt =4a ∫_0 ^(arcsin((√(2a)))) sin^(2n+2) t −4a ∫_0 ^(arcsinA) sin^(2n+4) tdt ⇒Σ_(k=0) ^n I_k =4a Σ_(k=0) ^n (v_k −v_(k+1) ) with v_k =∫_0 ^(arcsin((√(2a)))) sin^(2k+2) tdt =4a(v_0 −v_1 +v_1 −v_2 +....+v_n −v_(n+1) ) =4a (v_0 −v_(n+1) ) we have v_0 =∫_0 ^(arcsin((√(2a)))) sin^2 t dt =(1/2)∫_0 ^(arcsin((√(2a)))) (1+cos(2t))dt =((arcsin((√(2a))))/2) +[(1/4)sin(2t)]_0 ^(arcsin((√(2a)))) =((arcsin((√(2a))))/2) +(1/2)[sint (√(1−sin^2 t))]_0 ^(arcsin((√(2a)))) =((arcsin((√(2a))))/2) +(1/2){(√(2a))(√(1−2a))} v_(n+1) =∫_0 ^(arcsin((√(2a)))) sin^(2n+4) t dt (wallis integral on[0,arcsin((√(2a)))) also we can determine a recurrence relation between I_n](Q116783.png)
| ||
Question and Answers Forum | ||
Question Number 116710 by ravisoni505 last updated on 06/Oct/20 | ||
 | ||
Answered by maths mind last updated on 06/Oct/20 | ||
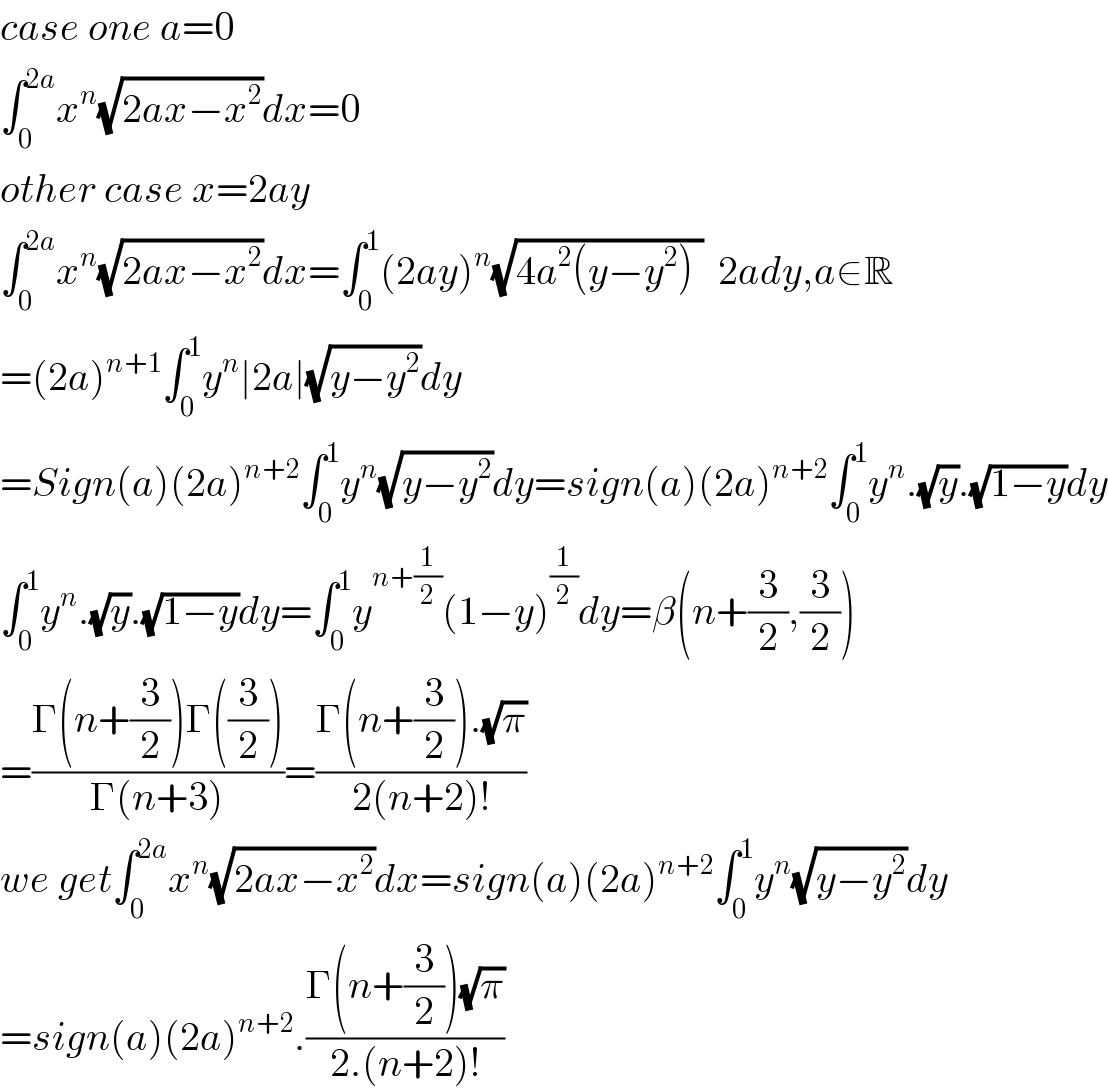 | ||
| ||
Answered by mathmax by abdo last updated on 06/Oct/20 | ||
![I_n =∫_0 ^(2a) x^n (√(2ax−x^2 )) dx ⇒ I_n =∫_0 ^(2a) x^n (√x)(√(2a−x))dx =_((√x)=t) ∫_0 ^(√(2a)) t^(2n) t(√(2a−t^2 ))2t dt =2 ∫_0 ^(√(2a)) t^(2n+2) (√(((√(2a)))^2 −t^2 ))dt =_(t=(√(2a))sinθ) 2 ∫_0 ^(arcsin((√(2a)))) sin^(2n+2) θ(√(2a))cost (√(2a))cost dt =4a ∫_0 ^(arcsin((√(2a)))) sin^(2n+2) cos^2 t dt =4a ∫_0 ^(arcsin((√(2a)))) sin^(2n+2) t(1−sin^2 t)dt =4a ∫_0 ^(arcsin((√(2a)))) sin^(2n+2) t −4a ∫_0 ^(arcsinA) sin^(2n+4) tdt ⇒Σ_(k=0) ^n I_k =4a Σ_(k=0) ^n (v_k −v_(k+1) ) with v_k =∫_0 ^(arcsin((√(2a)))) sin^(2k+2) tdt =4a(v_0 −v_1 +v_1 −v_2 +....+v_n −v_(n+1) ) =4a (v_0 −v_(n+1) ) we have v_0 =∫_0 ^(arcsin((√(2a)))) sin^2 t dt =(1/2)∫_0 ^(arcsin((√(2a)))) (1+cos(2t))dt =((arcsin((√(2a))))/2) +[(1/4)sin(2t)]_0 ^(arcsin((√(2a)))) =((arcsin((√(2a))))/2) +(1/2)[sint (√(1−sin^2 t))]_0 ^(arcsin((√(2a)))) =((arcsin((√(2a))))/2) +(1/2){(√(2a))(√(1−2a))} v_(n+1) =∫_0 ^(arcsin((√(2a)))) sin^(2n+4) t dt (wallis integral on[0,arcsin((√(2a)))) also we can determine a recurrence relation between I_n](Q116783.png) | ||
| ||