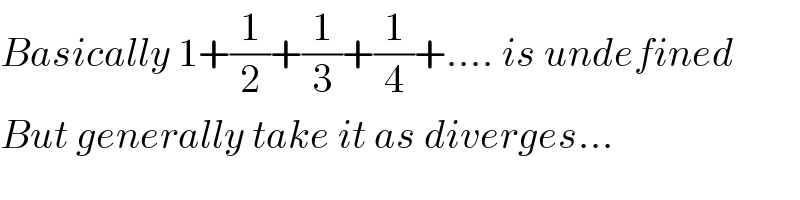Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 116725 by bemath last updated on 06/Oct/20

what the value of log _(10) (−1) in complex number

$$\mathrm{what}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{log}\:_{\mathrm{10}} \left(−\mathrm{1}\right)\:\mathrm{in}\: \\ $$$$\mathrm{complex}\:\mathrm{number} \\ $$

Commented by bemath last updated on 06/Oct/20

thank you prof

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{prof} \\ $$

Commented by MJS_new last updated on 06/Oct/20

usually we take the principal value z=re^(iθ) with r∈R^+ and −π≤θ<π [ ] ⇒ principal value of ln z =ln r +iθ and log_z_2 z_1 =((ln z_1 )/(ln z_2 ))=((ln r_1 e^(iθ_1 ) )/(ln r_2 e^(iθ_2 ) ))=((ln r_1 +iθ_1 )/(ln r_2 +iθ_2 ))= =((θ_1 θ_2 +ln r_1 ln r_2 )/(ln^2 r_2 +θ_2 ^2 ))+i((θ_1 ln r_2 −θ_2 ln r_1 )/(ln^2 r_2 +θ_2 ^2 )) with r_1 , r_2 >0

$$\mathrm{usually}\:\mathrm{we}\:\mathrm{take}\:\mathrm{the}\:\mathrm{principal}\:\mathrm{value} \\ $$$${z}={r}\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{with}\:{r}\in\mathbb{R}^{+} \:\mathrm{and}\:−\pi\leqslant\theta<\pi\:\left[\:\right] \\ $$$$\Rightarrow\:\mathrm{principal}\:\mathrm{value}\:\mathrm{of}\:\:\mathrm{ln}\:{z}\:=\mathrm{ln}\:{r}\:+\mathrm{i}\theta \\ $$$$\mathrm{and}\:\mathrm{log}_{{z}_{\mathrm{2}} } \:{z}_{\mathrm{1}} \:=\frac{\mathrm{ln}\:{z}_{\mathrm{1}} }{\mathrm{ln}\:{z}_{\mathrm{2}} }=\frac{\mathrm{ln}\:{r}_{\mathrm{1}} \mathrm{e}^{\mathrm{i}\theta_{\mathrm{1}} } }{\mathrm{ln}\:{r}_{\mathrm{2}} \mathrm{e}^{\mathrm{i}\theta_{\mathrm{2}} } }=\frac{\mathrm{ln}\:{r}_{\mathrm{1}} \:+\mathrm{i}\theta_{\mathrm{1}} }{\mathrm{ln}\:{r}_{\mathrm{2}} \:+\mathrm{i}\theta_{\mathrm{2}} }= \\ $$$$=\frac{\theta_{\mathrm{1}} \theta_{\mathrm{2}} +\mathrm{ln}\:{r}_{\mathrm{1}} \:\mathrm{ln}\:{r}_{\mathrm{2}} }{\mathrm{ln}^{\mathrm{2}} \:{r}_{\mathrm{2}} \:+\theta_{\mathrm{2}} ^{\mathrm{2}} }+\mathrm{i}\frac{\theta_{\mathrm{1}} \mathrm{ln}\:{r}_{\mathrm{2}} \:−\theta_{\mathrm{2}} \mathrm{ln}\:{r}_{\mathrm{1}} }{\mathrm{ln}^{\mathrm{2}} \:{r}_{\mathrm{2}} \:+\theta_{\mathrm{2}} ^{\mathrm{2}} } \\ $$$$\mathrm{with}\:{r}_{\mathrm{1}} ,\:{r}_{\mathrm{2}} \:>\mathrm{0} \\ $$

Commented by MJS_new last updated on 06/Oct/20

btw also ln e^r =r is “only” the principal value: e^r =e^r e^(2nπi) ⇒ ln e^r =r+2nπi but who would like to use this?

$$\mathrm{btw}\:\mathrm{also}\:\mathrm{ln}\:\mathrm{e}^{{r}} \:={r}\:\mathrm{is}\:``\mathrm{only}''\:\mathrm{the}\:\mathrm{principal} \\ $$$$\mathrm{value}:\:\mathrm{e}^{{r}} =\mathrm{e}^{{r}} \mathrm{e}^{\mathrm{2}{n}\pi\mathrm{i}} \:\Rightarrow\:\mathrm{ln}\:\mathrm{e}^{{r}} \:={r}+\mathrm{2}{n}\pi\mathrm{i}\:\mathrm{but} \\ $$$$\mathrm{who}\:\mathrm{would}\:\mathrm{like}\:\mathrm{to}\:\mathrm{use}\:\mathrm{this}? \\ $$

Answered by MJS_new last updated on 06/Oct/20

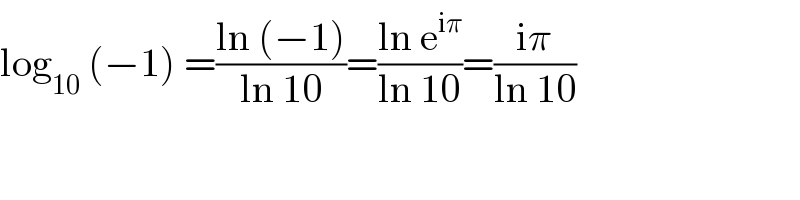
log_(10) (−1) =((ln (−1))/(ln 10))=((ln e^(iπ) )/(ln 10))=((iπ)/(ln 10))

$$\mathrm{log}_{\mathrm{10}} \:\left(−\mathrm{1}\right)\:=\frac{\mathrm{ln}\:\left(−\mathrm{1}\right)}{\mathrm{ln}\:\mathrm{10}}=\frac{\mathrm{ln}\:\mathrm{e}^{\mathrm{i}\pi} }{\mathrm{ln}\:\mathrm{10}}=\frac{\mathrm{i}\pi}{\mathrm{ln}\:\mathrm{10}} \\ $$

Commented by bemath last updated on 06/Oct/20

sir if log _(10) (0) = ?

$$\mathrm{sir}\:\mathrm{if}\:\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{0}\right)\:=\:?\: \\ $$

Commented by bemath last updated on 06/Oct/20

−1 = cos π+ i.sin π , sir

$$−\mathrm{1}\:=\:\mathrm{cos}\:\pi+\:{i}.\mathrm{sin}\:\pi\:,\:\mathrm{sir} \\ $$$$ \\ $$

Answered by TANMAY PANACEA last updated on 06/Oct/20

trying Log(a+ib) a=rcosθ b=rsinθ Log(re^(iθ) )=Log(re^(i(2kπ+θ)) )=logr+i(2kπ+θ) Log(a+ib)=log((√(a^2 +b^2 )) )+i{2kπ+tan^(−1) ((b/a))} Log(a+ib)=(1/2)log(a^2 +b^2 )+i(2kπ+tan^(−1) ((b/a))) log_(10) p×x=log_e p ((logp)/(log10))×x=((logp)/(loge))→x=log_e 10 log_(10) (−1)=log_e (−1)×log_(10) e log_(10) (−1) =log_e (−1)×log_(10) e =[(1/2)ln(1+0^2 )+i(2kπ+tan^(−1) (((−1)/0))]log_(10) e =[0+i(2kπ−(π/2))]log_(10) e

$${trying} \\ $$$${Log}\left({a}+{ib}\right) \\ $$$${a}={rcos}\theta\:\:\:{b}={rsin}\theta \\ $$$${Log}\left({re}^{{i}\theta} \right)={Log}\left({re}^{{i}\left(\mathrm{2}{k}\pi+\theta\right)} \right)={logr}+{i}\left(\mathrm{2}{k}\pi+\theta\right) \\ $$$${Log}\left({a}+{ib}\right)={log}\left(\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\right)+{i}\left\{\mathrm{2}{k}\pi+{tan}^{−\mathrm{1}} \left(\frac{{b}}{{a}}\right)\right\} \\ $$$${Log}\left({a}+{ib}\right)=\frac{\mathrm{1}}{\mathrm{2}}{log}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+{i}\left(\mathrm{2}{k}\pi+{tan}^{−\mathrm{1}} \left(\frac{{b}}{{a}}\right)\right) \\ $$$${log}_{\mathrm{10}} {p}×{x}={log}_{{e}} {p} \\ $$$$\frac{{logp}}{{log}\mathrm{10}}×{x}=\frac{{logp}}{{loge}}\rightarrow{x}={log}_{{e}} \mathrm{10} \\ $$$$\boldsymbol{{log}}_{\mathrm{10}} \left(−\mathrm{1}\right)=\boldsymbol{{log}}_{\boldsymbol{{e}}} \left(−\mathrm{1}\right)×\boldsymbol{{log}}_{\mathrm{10}} \boldsymbol{{e}} \\ $$$$\boldsymbol{{log}}_{\mathrm{10}} \left(−\mathrm{1}\right) \\ $$$$=\boldsymbol{{log}}_{\boldsymbol{{e}}} \left(−\mathrm{1}\right)×\boldsymbol{{log}}_{\mathrm{10}} \boldsymbol{{e}} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+\mathrm{0}^{\mathrm{2}} \right)+{i}\left(\mathrm{2}{k}\pi+{tan}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\mathrm{0}}\right)\right]{log}_{\mathrm{10}} {e}\right. \\ $$$$=\left[\mathrm{0}+{i}\left(\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{2}}\right)\right]{log}_{\mathrm{10}} {e} \\ $$$$ \\ $$$$ \\ $$

Commented by bemath last updated on 06/Oct/20

how about log _(10) (0) sir

$$\mathrm{how}\:\mathrm{about}\:\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{0}\right)\:\mathrm{sir} \\ $$

Commented by Rio Michael last updated on 06/Oct/20

now am sure log_(10) (0) should be undefined since ln (0) is undefined.

$$\mathrm{now}\:\mathrm{am}\:\mathrm{sure}\:\mathrm{log}_{\mathrm{10}} \left(\mathrm{0}\right)\:\mathrm{should}\:\mathrm{be}\:\mathrm{undefined} \\ $$$$\mathrm{since}\:\:\mathrm{ln}\:\left(\mathrm{0}\right)\:\mathrm{is}\:\mathrm{undefined}. \\ $$

Commented by Dwaipayan Shikari last updated on 06/Oct/20

Yes!

$${Yes}! \\ $$

Commented by bemath last updated on 06/Oct/20

ok. thank you all

$$\mathrm{ok}.\:\mathrm{thank}\:\mathrm{you}\:\mathrm{all} \\ $$

Answered by Rio Michael last updated on 06/Oct/20

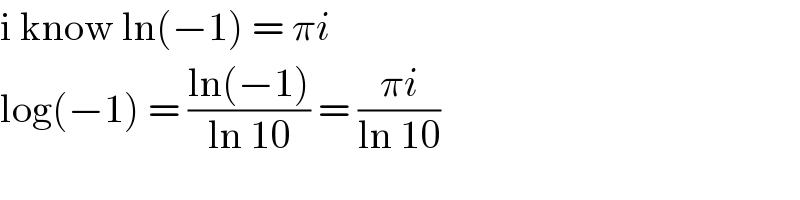
i know ln(−1) = πi log(−1) = ((ln(−1))/(ln 10)) = ((πi)/(ln 10))

$$\mathrm{i}\:\mathrm{know}\:\mathrm{ln}\left(−\mathrm{1}\right)\:=\:\pi{i} \\ $$$$\mathrm{log}\left(−\mathrm{1}\right)\:=\:\frac{\mathrm{ln}\left(−\mathrm{1}\right)}{\mathrm{ln}\:\mathrm{10}}\:=\:\frac{\pi{i}}{\mathrm{ln}\:\mathrm{10}} \\ $$

Answered by Dwaipayan Shikari last updated on 06/Oct/20

log_(10) (1−x)=((log(1−x))/(log10))=−(1/(log10))(x+(x^2 /2)+(x^3 /3)+....) X=1 −(1/(log10))(1+(1/2)+(1/3)+....)→−∞

$${log}_{\mathrm{10}} \left(\mathrm{1}−{x}\right)=\frac{{log}\left(\mathrm{1}−{x}\right)}{{log}\mathrm{10}}=−\frac{\mathrm{1}}{{log}\mathrm{10}}\left({x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+....\right) \\ $$$${X}=\mathrm{1} \\ $$$$−\frac{\mathrm{1}}{{log}\mathrm{10}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+....\right)\rightarrow−\infty \\ $$

Commented by Dwaipayan Shikari last updated on 06/Oct/20

Basically 1+(1/2)+(1/3)+(1/4)+.... is undefined But generally take it as diverges...

$${Basically}\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+....\:{is}\:{undefined} \\ $$$${But}\:{generally}\:{take}\:{it}\:{as}\:{diverges}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com