
Question Number 116822 by bemath last updated on 07/Oct/20

$$\:\mathrm{what}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\sqrt{{i}}\:=? \\ $$
Commented by Dwaipayan Shikari last updated on 07/Oct/20
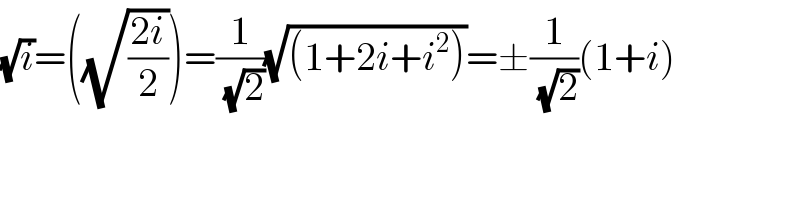
$$\sqrt{{i}}=\left(\sqrt{\frac{\mathrm{2}{i}}{\mathrm{2}}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{\left(\mathrm{1}+\mathrm{2}{i}+{i}^{\mathrm{2}} \right)}=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}+{i}\right) \\ $$
Answered by floor(10²Eta[1]) last updated on 07/Oct/20
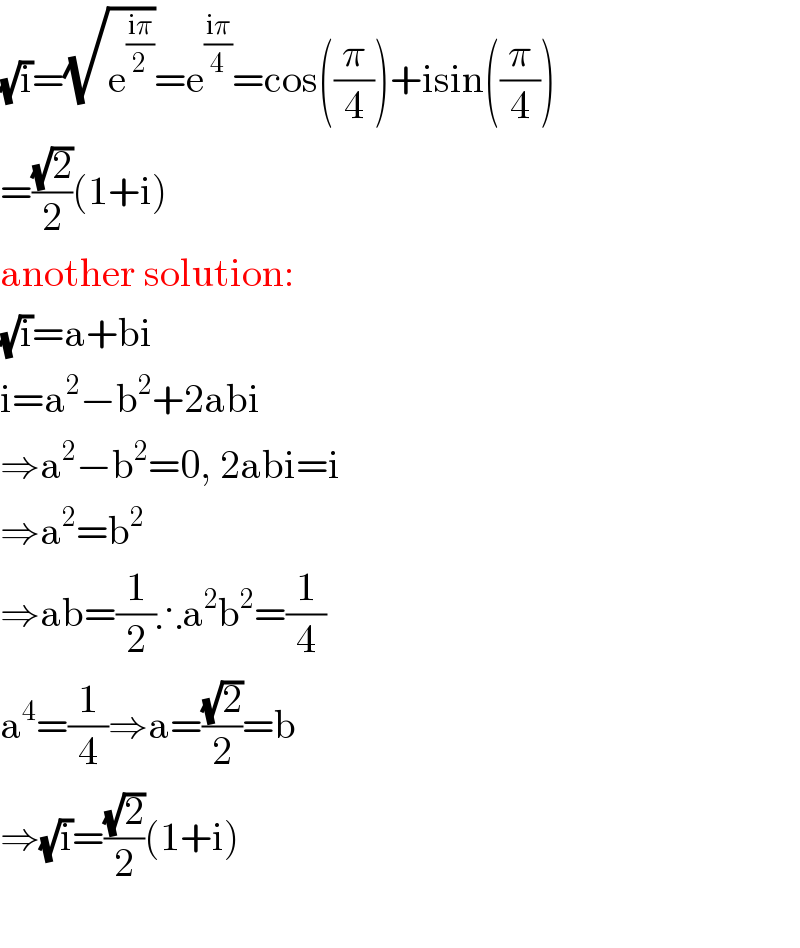
$$\sqrt{\mathrm{i}}=\sqrt{\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} }=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} =\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}\right)+\mathrm{isin}\left(\frac{\pi}{\mathrm{4}}\right) \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{i}\right) \\ $$$$\mathrm{another}\:\mathrm{solution}: \\ $$$$\sqrt{\mathrm{i}}=\mathrm{a}+\mathrm{bi} \\ $$$$\mathrm{i}=\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} +\mathrm{2abi} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} =\mathrm{0},\:\mathrm{2abi}=\mathrm{i} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{ab}=\frac{\mathrm{1}}{\mathrm{2}}\therefore\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{a}^{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\mathrm{a}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\mathrm{b} \\ $$$$\Rightarrow\sqrt{\mathrm{i}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{i}\right) \\ $$$$ \\ $$
Commented by bemath last updated on 07/Oct/20

$$\mathrm{gave}\:\mathrm{kudos} \\ $$
Answered by 1549442205PVT last updated on 07/Oct/20
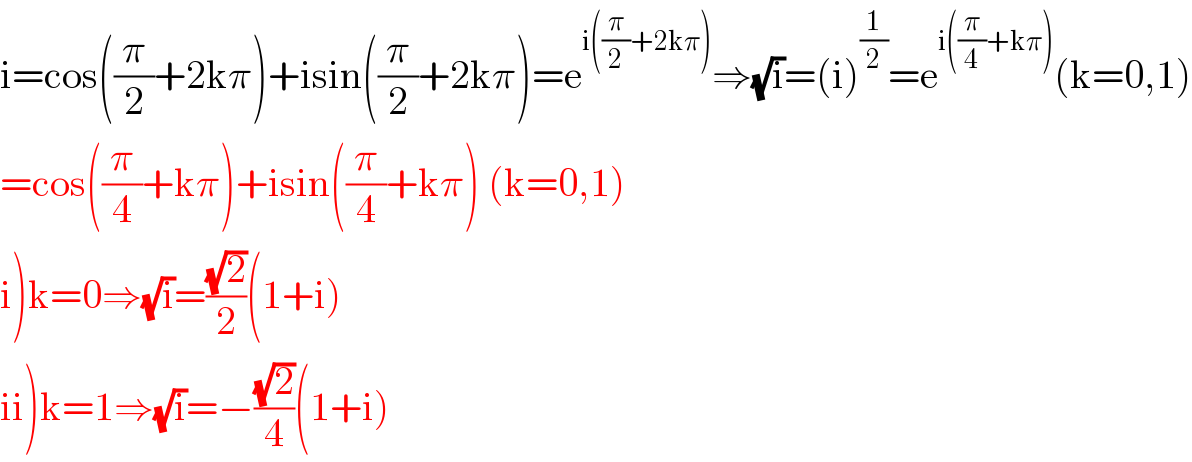
$$\mathrm{i}=\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}+\mathrm{2k}\pi\right)+\mathrm{isin}\left(\frac{\pi}{\mathrm{2}}+\mathrm{2k}\pi\right)=\mathrm{e}^{\mathrm{i}\left(\frac{\pi}{\mathrm{2}}+\mathrm{2k}\pi\right)} \Rightarrow\sqrt{\mathrm{i}}=\left(\mathrm{i}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{e}^{\mathrm{i}\left(\frac{\pi}{\mathrm{4}}+\mathrm{k}\pi\right)} \left(\mathrm{k}=\mathrm{0},\mathrm{1}\right) \\ $$$$=\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}+\mathrm{k}\pi\right)+\mathrm{isin}\left(\frac{\pi}{\mathrm{4}}+\mathrm{k}\pi\right)\:\left(\mathrm{k}=\mathrm{0},\mathrm{1}\right) \\ $$$$\left.\mathrm{i}\right)\mathrm{k}=\mathrm{0}\Rightarrow\sqrt{\mathrm{i}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{i}\right) \\ $$$$\left.\mathrm{ii}\right)\mathrm{k}=\mathrm{1}\Rightarrow\sqrt{\mathrm{i}}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{i}\right) \\ $$
Commented by bemath last updated on 07/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by 1549442205PVT last updated on 07/Oct/20

$$\mathrm{Thank}\:\mathrm{Sir}.\mathrm{You}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by malwaan last updated on 07/Oct/20
![(√i) = (√(((1/(√2)))^2 + i + ((i/(√2)))^2 )) = (√(((1/(√2)) + (i/(√2)))^2 )) = ± ((1/(√2)) + (i/(√2))) = (1/(√2))(1+i) =±((√2)/2)(1+i) another method i=[1 ; (π/2)] ⇒(√i) = [(√1) ; (((π/2) +2kπ)/2)] ; k=0 ; 1 k=0⇒[1 ; (π/4)]=cos(π/4) + isin(π/4) = ((√2)/2) + i((√2)/2) = ((√2)/2)(1+i) k=1⇒[1 ; ((5π)/4)]=cos((5π)/4)+isin((5π)/4) = − ((√2)/2) − i((√2)/2) = − ((√2)/2)(1+i) ∴ (√i) = ±((√2)/2)(1+i)](Q116831.png)
$$\sqrt{{i}}\:=\:\sqrt{\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\:{i}\:+\:\left(\frac{{i}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} } \\ $$$$\:=\:\sqrt{\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:+\:\frac{{i}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }\: \\ $$$$=\:\pm\:\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:+\:\frac{{i}}{\sqrt{\mathrm{2}}}\right)\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left(\mathrm{1}+{i}\right) \\ $$$$=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+{i}\right) \\ $$$${another}\:{method} \\ $$$${i}=\left[\mathrm{1}\:;\:\frac{\pi}{\mathrm{2}}\right] \\ $$$$\Rightarrow\sqrt{{i}}\:=\:\left[\sqrt{\mathrm{1}}\:;\:\frac{\frac{\pi}{\mathrm{2}}\:+\mathrm{2}{k}\pi}{\mathrm{2}}\right]\:;\:{k}=\mathrm{0}\:;\:\mathrm{1} \\ $$$${k}=\mathrm{0}\Rightarrow\left[\mathrm{1}\:;\:\frac{\pi}{\mathrm{4}}\right]={cos}\frac{\pi}{\mathrm{4}}\:+\:{isin}\frac{\pi}{\mathrm{4}} \\ $$$$\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:+\:{i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+{i}\right) \\ $$$${k}=\mathrm{1}\Rightarrow\left[\mathrm{1}\:;\:\frac{\mathrm{5}\pi}{\mathrm{4}}\right]={cos}\frac{\mathrm{5}\pi}{\mathrm{4}}+{isin}\frac{\mathrm{5}\pi}{\mathrm{4}} \\ $$$$=\:−\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:−\:{i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\:−\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+{i}\right) \\ $$$$\therefore\:\sqrt{{i}}\:=\:\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+{i}\right) \\ $$
Commented by bemath last updated on 07/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
