Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 116903 by mnjuly1970 last updated on 07/Oct/20

Answered by mathmax by abdo last updated on 07/Oct/20

let f(a) =∫_0 ^π ((ln(1+acosx))/(cosx)) dx (here a=sinα) ⇒ f^′ (a) =∫_0 ^π (dx/(1+acosx)) =_(tan((x/2))=t) ∫_0 ^∞ ((2dt)/((1+t^2 )(1+a.((1−t^2 )/(1+t^2 ))))) =2 ∫_0 ^∞ (dt/(1+t^2 +a−at^2 )) =2 ∫_0 ^∞ (dt/((1−a)t^2 +1+a)) =(2/(1−a))∫_0 ^∞ (dt/(t^2 +((1+a)/(1−a)))) =_(t =(√((1+a)/(1−a)))z) (2/(1−a))×((1−a)/(1+a))∫_0 ^∞ (1/(1+z^2 ))×((√(1+a))/(√(1−a)))dz =(2/(√(1−a^2 )))×(π/2) =(π/(√(1−a^2 ))) ⇒f(a) =π arcsin(a)+c c=f(0)=0 ⇒f(a) =π arcsina take a =sinα ⇒∫_0 ^π ((ln(1+sinα cosx))/(cosx))dx =π arcsin(sinα) =απ

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{acosx}\right)}{\mathrm{cosx}}\:\mathrm{dx}\:\:\left(\mathrm{here}\:\mathrm{a}=\mathrm{sin}\alpha\right)\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{acosx}}\:=_{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{a}.\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} +\mathrm{a}−\mathrm{at}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\left(\mathrm{1}−\mathrm{a}\right)\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}+\mathrm{a}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{1}+\mathrm{a}}{\mathrm{1}−\mathrm{a}}}\:=_{\mathrm{t}\:=\sqrt{\frac{\mathrm{1}+\mathrm{a}}{\mathrm{1}−\mathrm{a}}}\mathrm{z}} \:\:\:\frac{\mathrm{2}}{\mathrm{1}−\mathrm{a}}×\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }×\frac{\sqrt{\mathrm{1}+\mathrm{a}}}{\sqrt{\mathrm{1}−\mathrm{a}}}\mathrm{dz} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\pi\:\mathrm{arcsin}\left(\mathrm{a}\right)+\mathrm{c} \\ $$$$\mathrm{c}=\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\pi\:\mathrm{arcsina} \\ $$$$\mathrm{take}\:\mathrm{a}\:=\mathrm{sin}\alpha\:\Rightarrow\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{sin}\alpha\:\mathrm{cosx}\right)}{\mathrm{cosx}}\mathrm{dx}\:=\pi\:\mathrm{arcsin}\left(\mathrm{sin}\alpha\right)\:=\alpha\pi \\ $$

Commented by mnjuly1970 last updated on 08/Oct/20

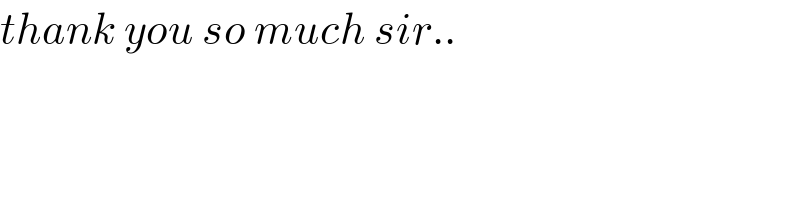
thank you so much sir..

$${thank}\:{you}\:{so}\:{much}\:{sir}.. \\ $$

Answered by Dwaipayan Shikari last updated on 08/Oct/20

∫_0 ^π ((log(1+sinacosx))/(cosx))dx I(Ψ)=∫_0 ^π ((log(1+Ψcosx))/(cosx))dx Ψ=sina I′(Ψ)=∫_0 ^π (1/((1+Ψcosx)))dx I′(Ψ)=2∫_0 ^∞ (1/((1+Ψ((1−t^2 )/(1+t^2 ))))).(1/(1+t^2 ))dt t=tan(x/2) I′(Ψ)=2∫_0 ^∞ (1/(1+t^2 +Ψt−Ψt^2 ))dt I′(Ψ)=(2/(1−Ψ))∫_0 ^∞ (1/(t^2 +((√((1+Ψ)/(1−Ψ))))^2 ))dt I′(Ψ)=(2/( (√(1−Ψ^2 ))))[tan^(−1) ((t(√(1−Ψ)))/( (√(1+Ψ))))]_0 ^∞ I′(Ψ)=(π/( (√(1−Ψ^2 )))) I(Ψ)=π∫(1/( (√(1−Ψ^2 ))))dΨ I(Ψ)=πsin^(−1) Ψ+C Ψ=sina I(Ψ)=πa+C a=0 then C=0 I(Ψ)=πa

$$\int_{\mathrm{0}} ^{\pi} \frac{{log}\left(\mathrm{1}+{sinacosx}\right)}{{cosx}}{dx} \\ $$$${I}\left(\Psi\right)=\int_{\mathrm{0}} ^{\pi} \frac{{log}\left(\mathrm{1}+\Psi{cosx}\right)}{{cosx}}{dx}\:\:\:\:\:\:\:\:\:\Psi={sina} \\ $$$${I}'\left(\Psi\right)=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{\left(\mathrm{1}+\Psi{cosx}\right)}{dx} \\ $$$${I}'\left(\Psi\right)=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+\Psi\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\:\:\:\:\:\:\:\:\:{t}={tan}\frac{{x}}{\mathrm{2}} \\ $$$${I}'\left(\Psi\right)=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} +\Psi{t}−\Psi{t}^{\mathrm{2}} }{dt} \\ $$$${I}'\left(\Psi\right)=\frac{\mathrm{2}}{\mathrm{1}−\Psi}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{t}^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{1}+\Psi}{\mathrm{1}−\Psi}}\right)^{\mathrm{2}} }{dt} \\ $$$${I}'\left(\Psi\right)=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\Psi^{\mathrm{2}} }}\left[{tan}^{−\mathrm{1}} \frac{{t}\sqrt{\mathrm{1}−\Psi}}{\:\sqrt{\mathrm{1}+\Psi}}\right]_{\mathrm{0}} ^{\infty} \\ $$$${I}'\left(\Psi\right)=\frac{\pi}{\:\sqrt{\mathrm{1}−\Psi^{\mathrm{2}} }} \\ $$$${I}\left(\Psi\right)=\pi\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\Psi^{\mathrm{2}} }}{d}\Psi \\ $$$${I}\left(\Psi\right)=\pi{sin}^{−\mathrm{1}} \Psi+{C}\:\:\:\:\Psi={sina} \\ $$$${I}\left(\Psi\right)=\pi{a}+{C} \\ $$$${a}=\mathrm{0}\:{then}\:{C}=\mathrm{0} \\ $$$${I}\left(\Psi\right)=\pi{a} \\ $$

Commented by mnjuly1970 last updated on 08/Oct/20

thank you mr dwaipayn...

$${thank}\:\:{you}\:{mr}\:{dwaipayn}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com