
Question and Answers Forum
Question Number 116930 by bobhans last updated on 08/Oct/20
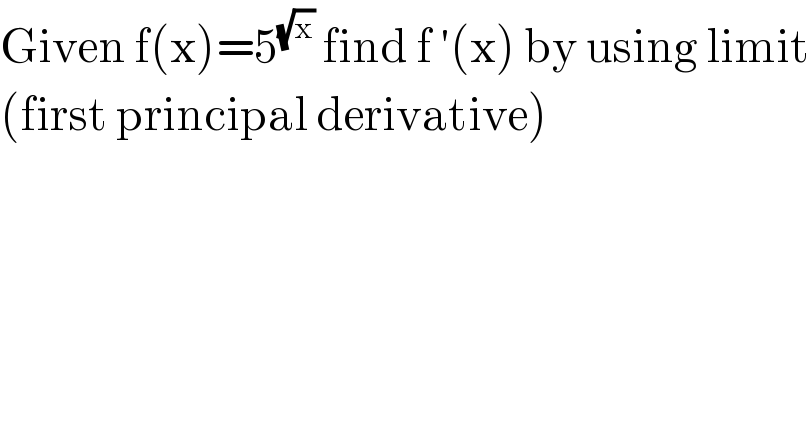
Commented by bobhans last updated on 08/Oct/20

Answered by 1549442205PVT last updated on 09/Oct/20
![First,we prove that lim _(x→0) ((a^x −1)/x)=lna. by using the definition of limit We can assume x>0(if x<0 put x=−t) Suppose ε>0 be an arbitrarily small number so that ∣((a^x −1)/x)−lna∣<ε.Then choosing δ=((ln[(−εx+xlna+1)^(−1) ])/(lna))>0 we have ∣x∣<δ⇔−((ln[(−εx+xlna+1)^(−1) ])/(lna))<x<((ln[(−εx+xlna+1)^(−1) ])/(lna)) ⇒−ln[(−εx+xlna+1)^(−1) ]<xlna<ln[(−εx+xlna+1)^(−1) ] ⇒ln(−εx+xlna+1)<lna^x <ln[(−εx+xlna+1)^(−1) ] ⇒−εx+xlna+1<a^x <(−εx+xlna+1)^(−1) ⇒−εx<a^x −1−xlna<εx (Since (−εx+xlna+1)^(−1) =(1/(−εx+xlna+1)) <−εx+xlna+1<εx+xlna+1) ⇒−ε<((a^x −1−xlna)/x)<ε⇒∣((a^x −1)/x)−lna∣<ε By the definition of the limit of a function we have: lim_(x→0) ((a^x −1)/x)=lna (Q.E.D)(1) Now by the definition of derivative of a function we have f ′(x)=lim{[f(x+Δx)−f(x)]/Δx}.Hence, (5^(√x) )′=lim_(Δu→0) ((5^(√(x+Δx)) −5^(√x) )/( Δx)) =lim_(Δx→0) ((5^(√x) (5^((√(x+Δx))−(√x)) −1))/( ((√(x+Δx))−(√x)).((Δx)/( (√(x+Δx))−(√x))))) =lim((5^(√x) (5^((√(x+Δx))−(√x)) −1))/( ((√(x+Δx))−(√x)).((Δx((√(x+Δx))+(√x)))/( (√(x+Δx))−(√x))((√(x+Δx))+(√x)))))) =lim((5^(√x) (5^((√(x+Δx))−(√x)) −1))/( ((√(x+Δx))−(√x)).((Δx((√(x+Δx))+(√x)))/( Δx)))) =lim_(Δx→0) (((5^(√x) (5^((√(x+Δx))−(√x)) −1))/( ((√(x+Δx))−(√x)).))).lim_(Δx→0) (1/( (√(x+Δx))+(√x))) =5^(√x) ln5.(1/(2(√x))) since lim_(Δx→0) (((5^((√(x+Δx))−(√x)) −1))/( ((√(x+Δx))−(√x)).))=ln5(by (1)) Thus,finally we obtained (a^(√x) )′=((5^(√x) ln5)/(2(√x))) is proved by limit](Q116932.png)
Commented by bemath last updated on 08/Oct/20
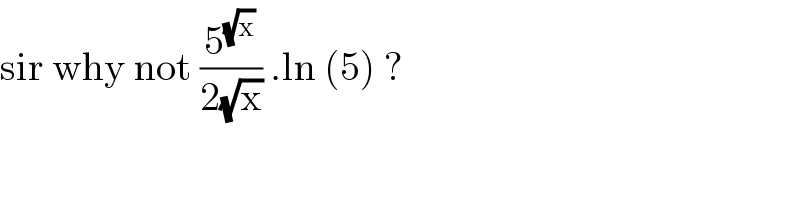
Commented by bemath last updated on 08/Oct/20
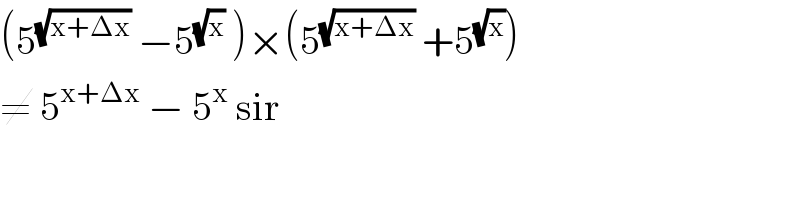
Commented by bobhans last updated on 08/Oct/20
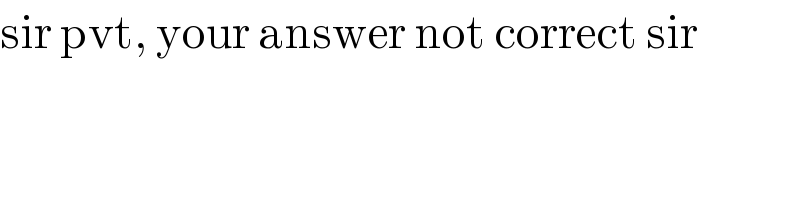
Commented by 1549442205PVT last updated on 08/Oct/20

Commented by bemath last updated on 08/Oct/20

Commented by bobhans last updated on 08/Oct/20
Commented by 1549442205PVT last updated on 09/Oct/20

Answered by TANMAY PANACEA last updated on 08/Oct/20
![(dy/dx)=lim_(h→0) ((5^((√(x+h)) ) −5^(√x) )/h) =lim_(h→0) 5^((√x) ) ×(((5^((√(x+h)) −(√x) ) −1)/h)) =5^((√x) ) ×lim_(t→0) (((5^t −1)/t))×lim_(h→0) ((((√(x+h)) −(√x) )/h))[t=(√(x+h)) −(√x) ] =5^((√x) ) ×lim_(t→0) (((e^(tln5) −1)/(tln5)))×ln5×lim_(h→0) ((h/h)×(1/( (√(x+h)) +(√x)))) =5^((√x) ) ×1×ln5×(1/(2(√x)))=5^((√x) ) ×ln5×(1/(2(√x)))](Q116943.png)
