
Question and Answers Forum
Question Number 116939 by joki last updated on 08/Oct/20
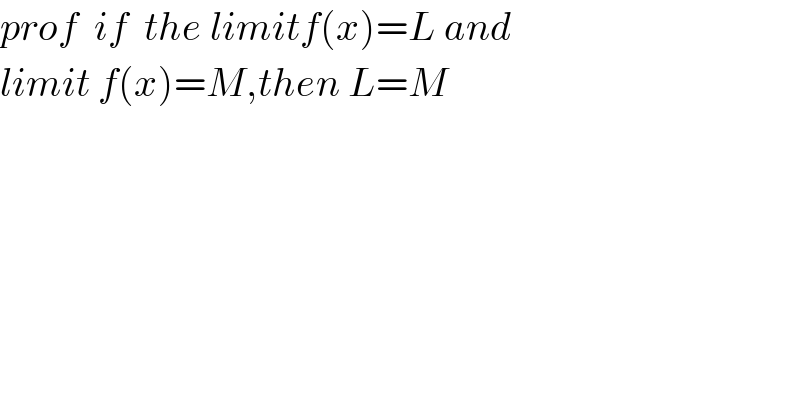
Answered by MAB last updated on 08/Oct/20
![lim_(x→x_0 ) f(x)=L=M ⇒[(∀ε>0)(∃α>0)(∀x∈D_f ):∣x−x_0 ∣<α⇒∣f(x)−L ∣<ε] and [(∀ε′>0)(∃α′>0)(∀x∈D_f ):∣x−x_0 ∣<α′⇒∣f(x)−M ∣<ε′] we have ∣M−L∣≤∣f(x)−L∣+f(x)−M∣ triangle inequality hence (∀ε>0)(∃δ=min(α,α′)>0): ∣x−x_0 ∣<δ⇒∣M−L∣<∍ finally M=L](Q116944.png)
Answered by MAB last updated on 08/Oct/20
![lim_(x→x_0 ) f(x)=L=M ⇒[(∀ε>0)(∃α>0)(∀x∈D_f ):∣x−x_0 ∣<α⇒∣f(x)−L ∣<ε] and [(∀ε′>0)(∃α′>0)(∀x∈D_f ):∣x−x_0 ∣<α′⇒∣f(x)−M ∣<ε′] we have ∣M−L∣≤∣f(x)−L∣+f(x)−M∣ triangle inequality hence (∀ε>0)(∃δ=min(α,α′)>0): ∣x−x_0 ∣<δ⇒∣M−L∣<∍ finally M=L](Q116945.png)
| ||
Question and Answers Forum | ||
Question Number 116939 by joki last updated on 08/Oct/20 | ||
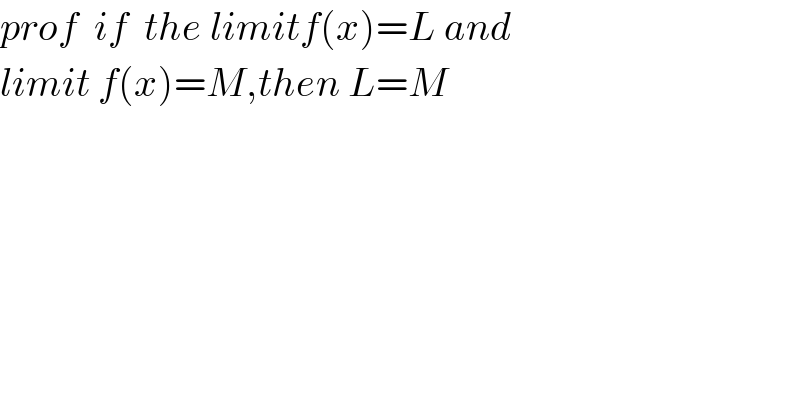 | ||
Answered by MAB last updated on 08/Oct/20 | ||
![lim_(x→x_0 ) f(x)=L=M ⇒[(∀ε>0)(∃α>0)(∀x∈D_f ):∣x−x_0 ∣<α⇒∣f(x)−L ∣<ε] and [(∀ε′>0)(∃α′>0)(∀x∈D_f ):∣x−x_0 ∣<α′⇒∣f(x)−M ∣<ε′] we have ∣M−L∣≤∣f(x)−L∣+f(x)−M∣ triangle inequality hence (∀ε>0)(∃δ=min(α,α′)>0): ∣x−x_0 ∣<δ⇒∣M−L∣<∍ finally M=L](Q116944.png) | ||
| ||
Answered by MAB last updated on 08/Oct/20 | ||
![lim_(x→x_0 ) f(x)=L=M ⇒[(∀ε>0)(∃α>0)(∀x∈D_f ):∣x−x_0 ∣<α⇒∣f(x)−L ∣<ε] and [(∀ε′>0)(∃α′>0)(∀x∈D_f ):∣x−x_0 ∣<α′⇒∣f(x)−M ∣<ε′] we have ∣M−L∣≤∣f(x)−L∣+f(x)−M∣ triangle inequality hence (∀ε>0)(∃δ=min(α,α′)>0): ∣x−x_0 ∣<δ⇒∣M−L∣<∍ finally M=L](Q116945.png) | ||
| ||