Question Number 116998 by TANMAY PANACEA last updated on 08/Oct/20
$$\int_{\frac{−\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sin}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{2}^{{x}} }{dx} \\ $$
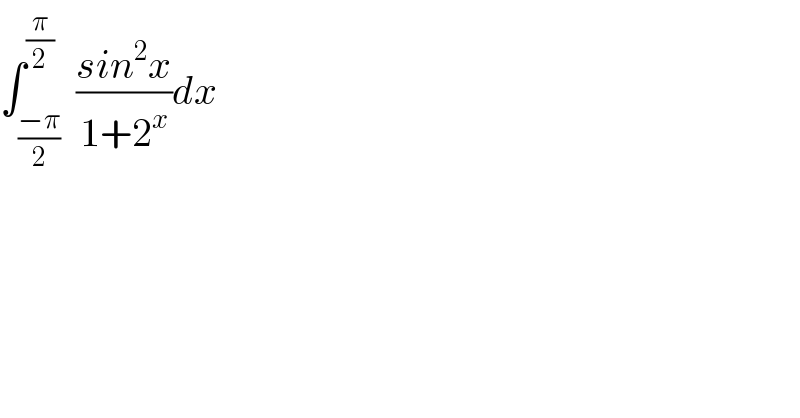
Commented by Dwaipayan Shikari last updated on 08/Oct/20
$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{2}^{{x}} }{dx}=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{2}^{−{x}} }{dx} \\ $$$$\mathrm{2}{I}=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} {xdx} \\ $$$$\mathrm{2}{I}=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}−{cos}\mathrm{2}{x}}{\mathrm{2}} \\ $$$$\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} {sin}\mathrm{2}{x} \\ $$$${I}=\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
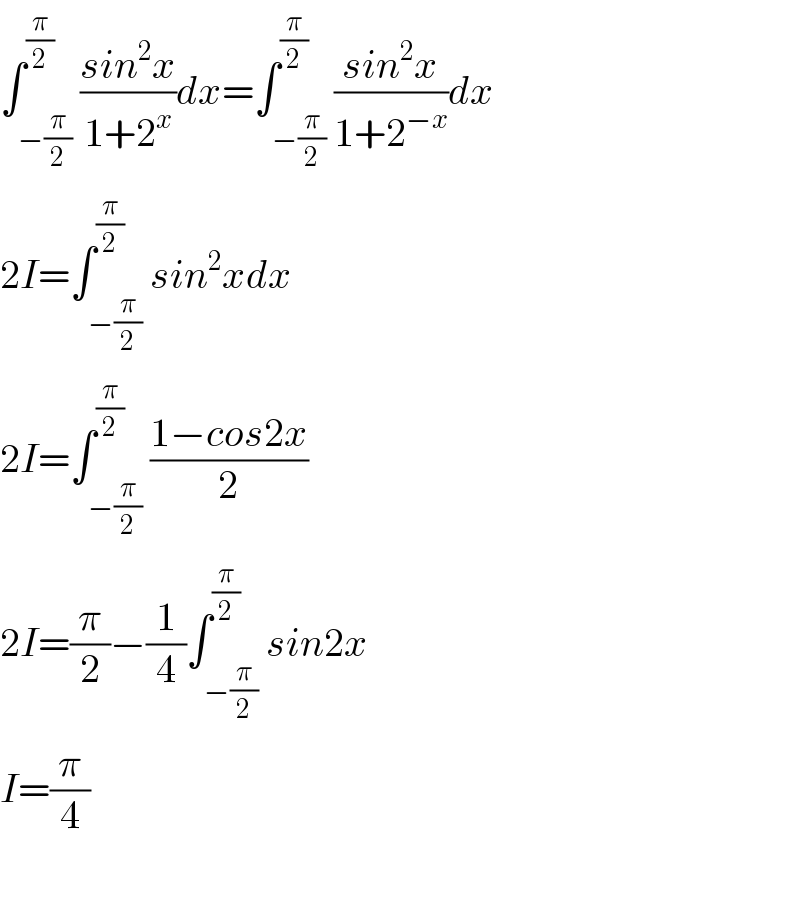
Commented by TANMAY PANACEA last updated on 08/Oct/20
$${thank}\:{you} \\ $$
Answered by TANMAY PANACEA last updated on 08/Oct/20
$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{b}} {f}\left({a}+{b}−{x}\right){dx} \\ $$$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sin}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{2}^{−\boldsymbol{{x}}} }\boldsymbol{{dx}} \\ $$$$\mathrm{2}\boldsymbol{{I}}=\int_{\frac{−\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}^{\mathrm{2}} {x}\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{{x}} }+\frac{\mathrm{2}^{{x}} }{\mathrm{2}^{{x}} +\mathrm{1}}\right){dx} \\ $$$$\mathrm{2}{I}=\int_{\frac{−\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}−{cos}\mathrm{2}{x}}{\mathrm{2}}{dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}}\mid{x}−\frac{{sin}\mathrm{2}{x}}{\mathrm{2}}\mid_{\frac{−\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\mathrm{1}}{\mathrm{4}}\left(\pi\right) \\ $$
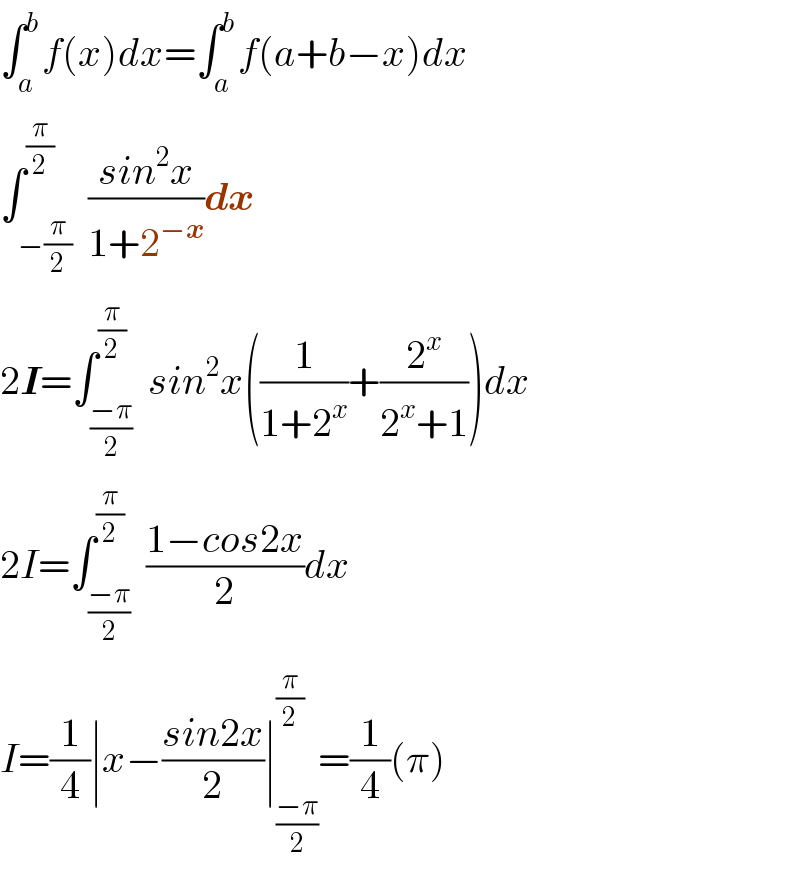
Answered by mathmax by abdo last updated on 08/Oct/20
![let∫_(−(π/2)) ^(π/2) ((sin^2 x)/(1+2^x ))dx =I changement x=−t give I =∫_(−(π/2)) ^(π/2) ((sin^2 t)/(1+2^(−t) ))dt ⇒2I =∫_(−(π/2)) ^(π/2) ((sin^2 x)/(1+2^x )) dx +∫_(−(π/2)) ^(π/2) ((sin^2 x)/(1+2^(−x) ))dx =∫_(−(π/2)) ^(π/2) ((1/(1+2^x ))+(1/(1+2^(−x) )))sin^2 x dx =∫_(−(π/2)) ^(π/2) (((2+2^x +2^(−x) )/(1+2^(−x) +2^x +1)))sin^2 x dx =∫_(−(π/2)) ^(π/2) ((1−cos(2x))/2)dx =(π/2)−(1/4)[sin(2x)]_(−(π/2)) ^(π/2) =(π/2) ⇒2I =(π/2) ⇒★I =(π/4) ★](Q117015.png)
$$\mathrm{let}\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}+\mathrm{2}^{\mathrm{x}} }\mathrm{dx}\:=\mathrm{I}\:\mathrm{changement}\:\mathrm{x}=−\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}{\mathrm{1}+\mathrm{2}^{−\mathrm{t}} }\mathrm{dt}\:\Rightarrow\mathrm{2I}\:=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}+\mathrm{2}^{\mathrm{x}} }\:\mathrm{dx}\:+\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}+\mathrm{2}^{−\mathrm{x}} }\mathrm{dx} \\ $$$$=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\mathrm{x}} }+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{−\mathrm{x}} }\right)\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}\:=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{2}+\mathrm{2}^{\mathrm{x}} +\mathrm{2}^{−\mathrm{x}} }{\mathrm{1}+\mathrm{2}^{−\mathrm{x}} \:+\mathrm{2}^{\mathrm{x}} \:+\mathrm{1}}\right)\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\mathrm{dx}\:=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{sin}\left(\mathrm{2x}\right)\right]_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{2}}\:\Rightarrow\mathrm{2I}\:=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\bigstar\mathrm{I}\:=\frac{\pi}{\mathrm{4}}\:\bigstar \\ $$
Commented by TANMAY PANACEA last updated on 08/Oct/20
$${thank}\:{you}\:{sir} \\ $$
Commented by Bird last updated on 09/Oct/20
$${you}\:{are}\:{welcome} \\ $$