
Question and Answers Forum
Question Number 116999 by TANMAY PANACEA last updated on 08/Oct/20
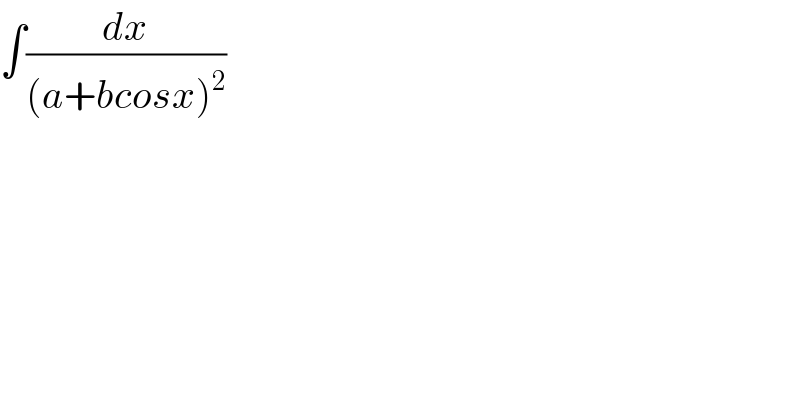
Answered by Olaf last updated on 08/Oct/20
![I(x) = ∫(dx/((a+b((e^(ix) +e^(−ix) )/2))^2 )) u = e^(ix) du = ie^(ix) dx = iudx dx = −i(du/u) I(u) = −i∫((du/u)/((a+b((u+(1/u))/2))^2 )) I(u) = −i∫((udu)/((au+b((u^2 +1)/2))^2 )) I(u) = −i∫((4udu)/((bu^2 +2au+b)^2 )) I(u) = −((4i)/b^2 )∫((4udu)/([(u+(a/b))^2 +1−(a^2 /b^2 )]^2 )) Different cases in function of sign of 1−(a^2 /b^2 )...](Q117018.png)
Answered by mathmax by abdo last updated on 08/Oct/20

Answered by TANMAY PANACEA last updated on 09/Oct/20

| ||
Question and Answers Forum | ||
Question Number 116999 by TANMAY PANACEA last updated on 08/Oct/20 | ||
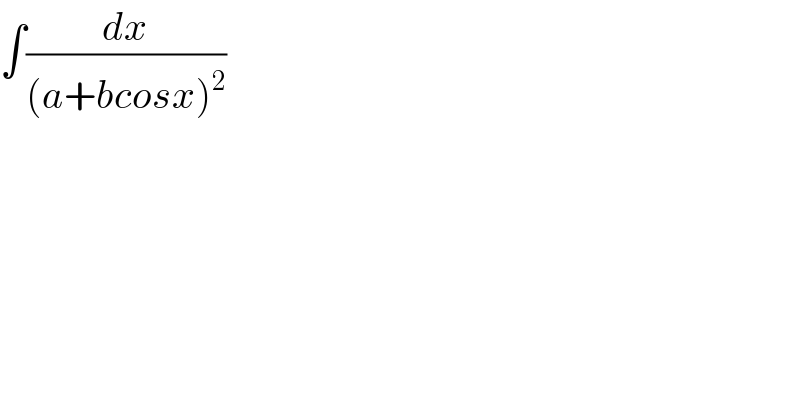 | ||
Answered by Olaf last updated on 08/Oct/20 | ||
![I(x) = ∫(dx/((a+b((e^(ix) +e^(−ix) )/2))^2 )) u = e^(ix) du = ie^(ix) dx = iudx dx = −i(du/u) I(u) = −i∫((du/u)/((a+b((u+(1/u))/2))^2 )) I(u) = −i∫((udu)/((au+b((u^2 +1)/2))^2 )) I(u) = −i∫((4udu)/((bu^2 +2au+b)^2 )) I(u) = −((4i)/b^2 )∫((4udu)/([(u+(a/b))^2 +1−(a^2 /b^2 )]^2 )) Different cases in function of sign of 1−(a^2 /b^2 )...](Q117018.png) | ||
| ||
Answered by mathmax by abdo last updated on 08/Oct/20 | ||
 | ||
| ||
Answered by TANMAY PANACEA last updated on 09/Oct/20 | ||
 | ||
| ||