Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 117085 by mohammad17 last updated on 09/Oct/20

Answered by Dwaipayan Shikari last updated on 09/Oct/20

∫_(−∞) ^∞ (1/(1+x^2 ))dx =[tan^(−1) x]_(−∞) ^∞ =π

$$\int_{−\infty} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\left[{tan}^{−\mathrm{1}} {x}\right]_{−\infty} ^{\infty} =\pi \\ $$

Answered by Dwaipayan Shikari last updated on 09/Oct/20

1. f(x)=log((1+x)/(1−x)) ((1+x)/(1−x))≥1 1+x≥1−x 2x≥0⇒x≥0 −1<x<1(Domain) 2. f(x)=(1/((1−x)^2 )) [ (x≠1)] Domain=R−{1} 3. f(x)=(1/(x^2 −3x+2)) f(x)=(1/((x−2)(x−1))) f(x)(Domain) =R−({1}and{2})

$$\mathrm{1}.\:\:\:\:\:\:\:\:\:\:\:\:{f}\left({x}\right)={log}\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}} \\ $$$$\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\geqslant\mathrm{1} \\ $$$$\mathrm{1}+{x}\geqslant\mathrm{1}−{x} \\ $$$$\mathrm{2}{x}\geqslant\mathrm{0}\Rightarrow{x}\geqslant\mathrm{0} \\ $$$$−\mathrm{1}<{x}<\mathrm{1}\left({Domain}\right) \\ $$$$\mathrm{2}.\:\:\:\:\:\:\:\:\:\:{f}\left({x}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\:\left[\:\:\left({x}\neq\mathrm{1}\right)\right] \\ $$$${Domain}=\mathbb{R}−\left\{\mathrm{1}\right\} \\ $$$$\mathrm{3}. \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)} \\ $$$${f}\left({x}\right)\left({Domain}\right)\:=\mathbb{R}−\left(\left\{\mathrm{1}\right\}{and}\left\{\mathrm{2}\right\}\right) \\ $$

Answered by Bird last updated on 10/Oct/20

f(x)=ln(((1+x)/(1−x))) ⇒f(x)=ln(1+x)−ln(1−x) we have (d/dx)ln(1+x)=(1/(1+x))=Σ_(n=0) ^∞ (−1)^n x^n ⇒ln(1+x) =Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) slso ln(1−x) =Σ_(n=1) ^∞ (((−1)^(n−1) (−x)^n )/n) =−Σ_(n=1) ^∞ (x^n /n) ⇒ f(x) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n +Σ_(n=1) ^∞ (x^n /n) =Σ_(n=1) ^∞ (1−(−1)^n )(x^n /n) =2 Σ_(n=0) ^∞ (x^(2n+1) /(2n+1))

$${f}\left({x}\right)={ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)\:\Rightarrow{f}\left({x}\right)={ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}−{x}\right) \\ $$$${we}\:{have}\:\frac{{d}}{{dx}}{ln}\left(\mathrm{1}+{x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}}=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \\ $$$$\Rightarrow{ln}\left(\mathrm{1}+{x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{x}^{{n}} }{{n}} \\ $$$${slso}\:{ln}\left(\mathrm{1}−{x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left(−{x}\right)^{{n}} }{{n}} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{x}^{{n}} +\sum_{{n}=\mathrm{1}} ^{\infty} \frac{{x}^{{n}} }{{n}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}−\left(−\mathrm{1}\right)^{{n}} \right)\frac{{x}^{{n}} }{{n}} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$

Answered by Bird last updated on 10/Oct/20

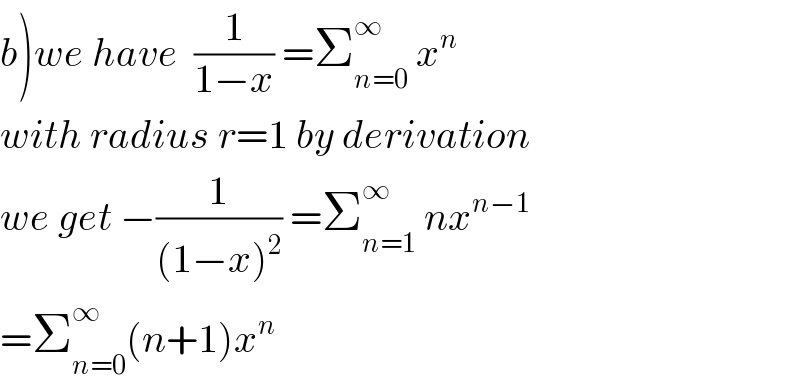
b)we have (1/(1−x)) =Σ_(n=0) ^∞ x^n with radius r=1 by derivation we get −(1/((1−x)^2 )) =Σ_(n=1) ^∞ nx^(n−1) =Σ_(n=0) ^∞ (n+1)x^n

$$\left.{b}\right){we}\:{have}\:\:\frac{\mathrm{1}}{\mathrm{1}−{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} \\ $$$${with}\:{radius}\:{r}=\mathrm{1}\:{by}\:{derivation} \\ $$$${we}\:{get}\:−\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}−\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \left({n}+\mathrm{1}\right){x}^{{n}} \\ $$

Answered by Bird last updated on 10/Oct/20

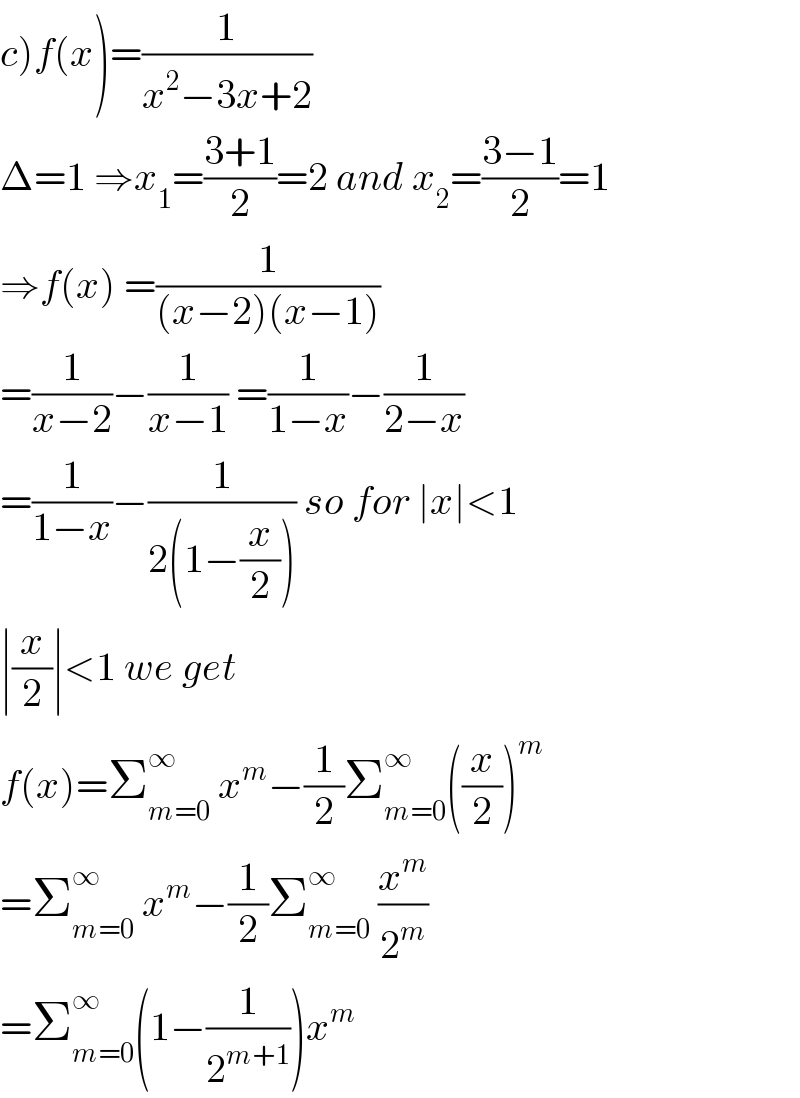
c)f(x)=(1/(x^2 −3x+2)) Δ=1 ⇒x_1 =((3+1)/2)=2 and x_2 =((3−1)/2)=1 ⇒f(x) =(1/((x−2)(x−1))) =(1/(x−2))−(1/(x−1)) =(1/(1−x))−(1/(2−x)) =(1/(1−x))−(1/(2(1−(x/2)))) so for ∣x∣<1 ∣(x/2)∣<1 we get f(x)=Σ_(m=0) ^∞ x^m −(1/2)Σ_(m=0) ^∞ ((x/2))^m =Σ_(m=0) ^(∞ ) x^m −(1/2)Σ_(m=0) ^∞ (x^m /2^m ) =Σ_(m=0) ^∞ (1−(1/2^(m+1) ))x^m

$$\left.{c}\right){f}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}} \\ $$$$\Delta=\mathrm{1}\:\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{1}}{\mathrm{2}}=\mathrm{2}\:{and}\:{x}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{1}}{\mathrm{2}}=\mathrm{1} \\ $$$$\Rightarrow{f}\left({x}\right)\:=\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{{x}−\mathrm{2}}−\frac{\mathrm{1}}{{x}−\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{1}−{x}}−\frac{\mathrm{1}}{\mathrm{2}−{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{x}}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)}\:{so}\:{for}\:\mid{x}\mid<\mathrm{1} \\ $$$$\mid\frac{{x}}{\mathrm{2}}\mid<\mathrm{1}\:{we}\:{get} \\ $$$${f}\left({x}\right)=\sum_{{m}=\mathrm{0}} ^{\infty} \:{x}^{{m}} −\frac{\mathrm{1}}{\mathrm{2}}\sum_{{m}=\mathrm{0}} ^{\infty} \left(\frac{{x}}{\mathrm{2}}\right)^{{m}} \\ $$$$=\sum_{{m}=\mathrm{0}} ^{\infty\:} \:{x}^{{m}} −\frac{\mathrm{1}}{\mathrm{2}}\sum_{{m}=\mathrm{0}} ^{\infty} \:\frac{{x}^{{m}} }{\mathrm{2}^{{m}} } \\ $$$$=\sum_{{m}=\mathrm{0}} ^{\infty} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{m}+\mathrm{1}} }\right){x}^{{m}} \\ $$

Answered by Bird last updated on 10/Oct/20

ex2 ∫_(−∞) ^(+∞) (dx/(1+x^2 )) =[arctanx]_(−∞) ^(+∞) =(π/2)+(π/2)=π f(z) =(1/(z^n +1)) poles of f! z^n +1 =0 ⇒z^(n ) =e^(i(2k+1)π) ⇒ z_k =e^(i(((2k+1)π)/n)) and k ∈[[0,n−1]]

$${ex}\mathrm{2}\:\:\:\:\:\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\left[{arctanx}\right]_{−\infty} ^{+\infty} \\ $$$$=\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}=\pi \\ $$$${f}\left({z}\right)\:=\frac{\mathrm{1}}{{z}^{{n}} \:+\mathrm{1}}\:{poles}\:{of}\:{f}! \\ $$$${z}^{{n}} +\mathrm{1}\:=\mathrm{0}\:\Rightarrow{z}^{{n}\:} ={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow \\ $$$${z}_{{k}} ={e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}} \:{and}\:{k}\:\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right] \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com