
Question and Answers Forum
Question Number 117100 by bemath last updated on 09/Oct/20
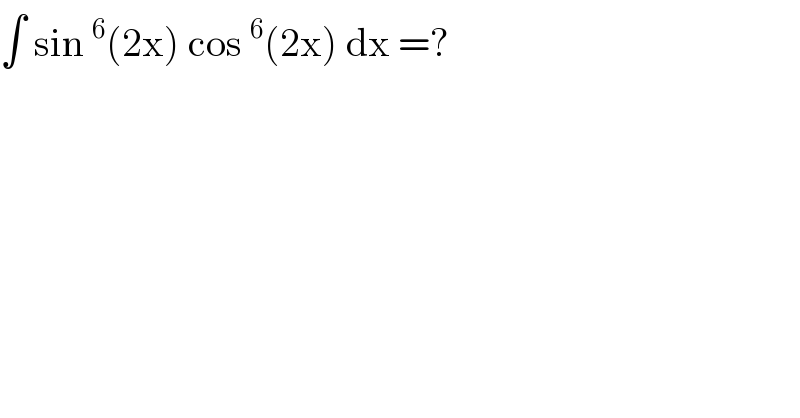
Answered by Dwaipayan Shikari last updated on 09/Oct/20
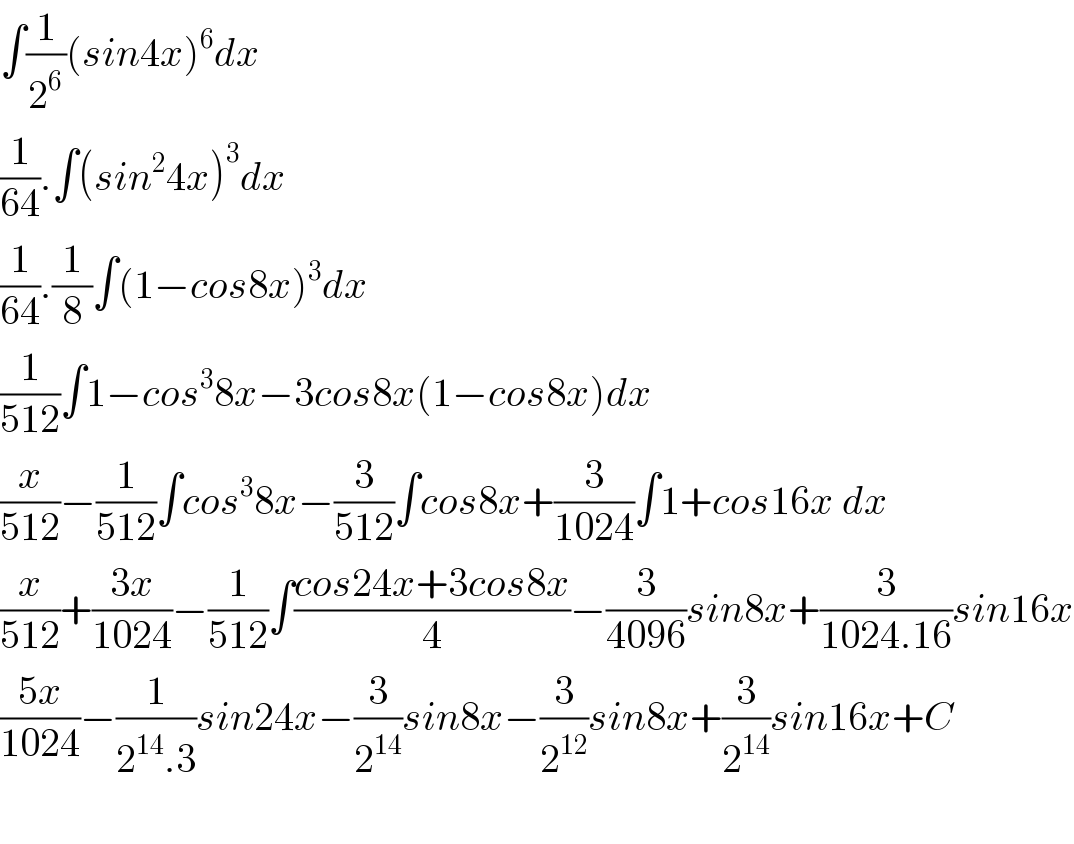
Answered by 1549442205PVT last updated on 09/Oct/20
![F=∫ sin^6 (2x) cos^6 (2x) dx = =(1/(64))∫[2sin(2x)cos(2x)]^6 dx =(1/(64))∫sin^6 (4x)dx= _(put 4x=t) (1/(256))∫sin^6 tdt =(1/(256)).(1/8)∫(1−cos2t)^3 dt =(1/2^(11) )∫(1−3cos2t+3cos^2 2t−cos^3 2t)dt =(1/2^(11) )[∫dt−(3/2)∫cos(2t)d(2t)+(3/2)∫(1+cos(4t))dt] −(1/2^(11) ).(1/2)∫(1−sin^2 2t)d(sin2t)) =(1/2^(11) )[t−(3/2)sin2t+(3/2)t+(3/8)sin4t] −(1/2^(12) )(sin2t−((sin^3 2t)/3)) =(5/2^(12) ) (4x)−(3/2^(12) )sin8x+(3/2^(14) )sin(16x) −(1/2^(12) )sin8t+(1/2^(12) )sin^3 8t =((5x)/2^(10) )−(1/2^(10) )sin8x+(1/2^(12) )sin^3 8x+(3/2^(14) )sin16x+C](Q117110.png)
Answered by Bird last updated on 10/Oct/20

| ||
Question and Answers Forum | ||
Question Number 117100 by bemath last updated on 09/Oct/20 | ||
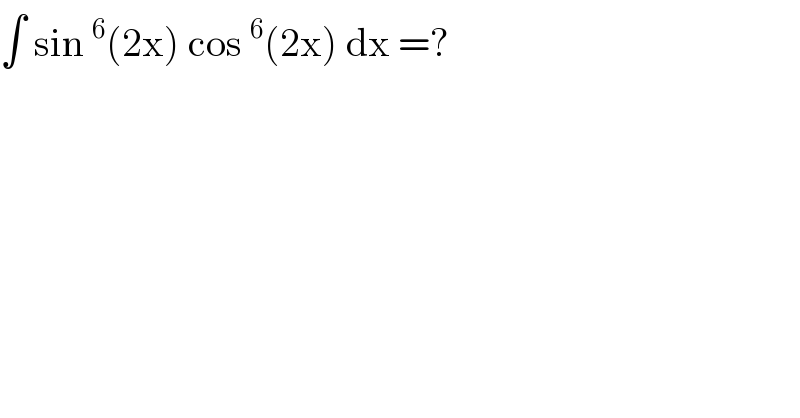 | ||
Answered by Dwaipayan Shikari last updated on 09/Oct/20 | ||
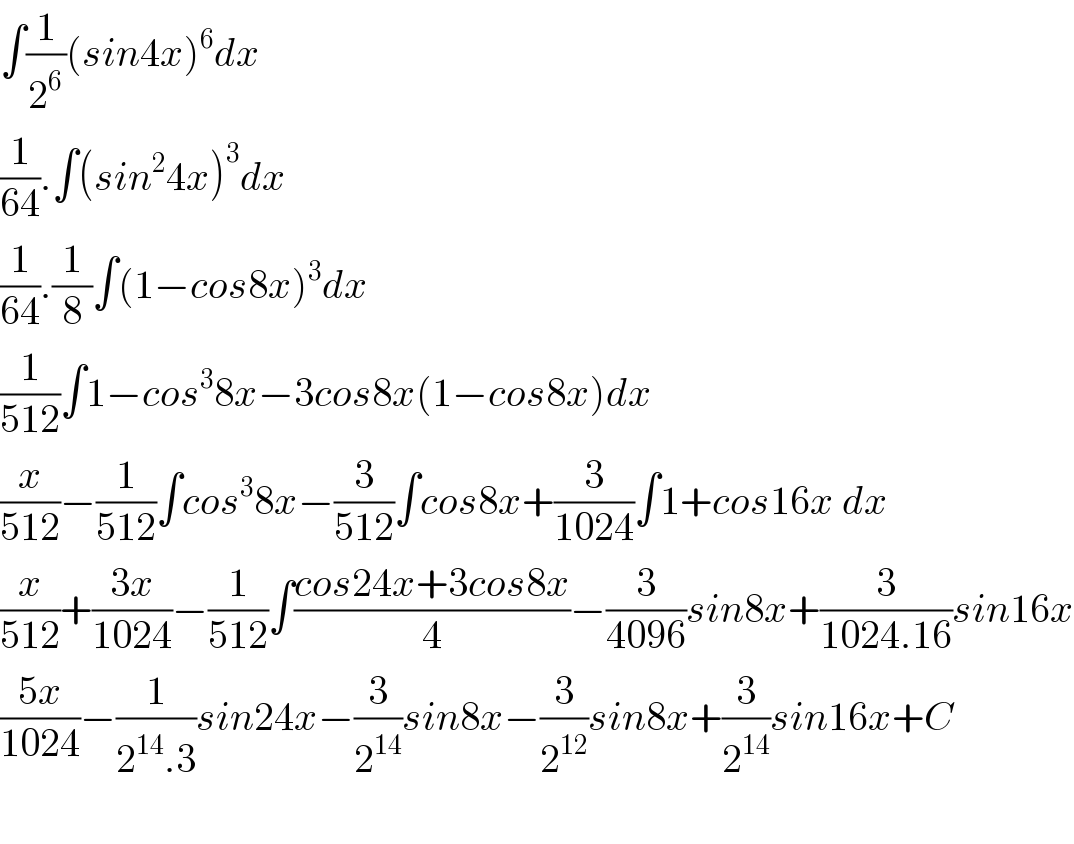 | ||
| ||
Answered by 1549442205PVT last updated on 09/Oct/20 | ||
![F=∫ sin^6 (2x) cos^6 (2x) dx = =(1/(64))∫[2sin(2x)cos(2x)]^6 dx =(1/(64))∫sin^6 (4x)dx= _(put 4x=t) (1/(256))∫sin^6 tdt =(1/(256)).(1/8)∫(1−cos2t)^3 dt =(1/2^(11) )∫(1−3cos2t+3cos^2 2t−cos^3 2t)dt =(1/2^(11) )[∫dt−(3/2)∫cos(2t)d(2t)+(3/2)∫(1+cos(4t))dt] −(1/2^(11) ).(1/2)∫(1−sin^2 2t)d(sin2t)) =(1/2^(11) )[t−(3/2)sin2t+(3/2)t+(3/8)sin4t] −(1/2^(12) )(sin2t−((sin^3 2t)/3)) =(5/2^(12) ) (4x)−(3/2^(12) )sin8x+(3/2^(14) )sin(16x) −(1/2^(12) )sin8t+(1/2^(12) )sin^3 8t =((5x)/2^(10) )−(1/2^(10) )sin8x+(1/2^(12) )sin^3 8x+(3/2^(14) )sin16x+C](Q117110.png) | ||
| ||
Answered by Bird last updated on 10/Oct/20 | ||
 | ||
| ||