Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 117122 by Ar Brandon last updated on 09/Oct/20

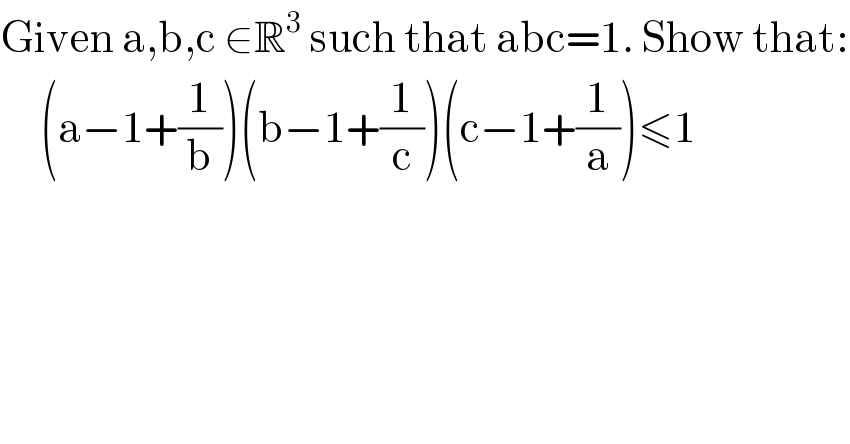
Given a,b,c ∈R^3 such that abc=1. Show that: (a−1+(1/b))(b−1+(1/c))(c−1+(1/a))≤1

$$\mathrm{Given}\:\mathrm{a},\mathrm{b},\mathrm{c}\:\in\mathbb{R}^{\mathrm{3}} \:\mathrm{such}\:\mathrm{that}\:\mathrm{abc}=\mathrm{1}.\:\mathrm{Show}\:\mathrm{that}: \\ $$$$\:\:\:\:\:\left(\mathrm{a}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{b}}\right)\left(\mathrm{b}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{c}}\right)\left(\mathrm{c}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{a}}\right)\leqslant\mathrm{1} \\ $$

Commented by MJS_new last updated on 09/Oct/20

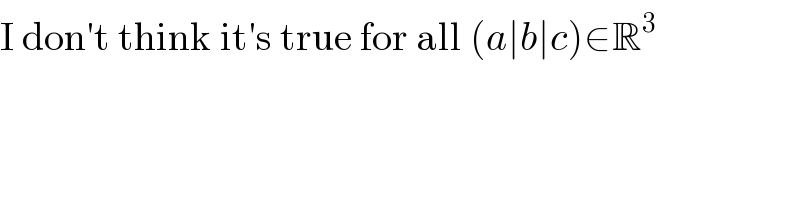
I don′t think it′s true for all (a∣b∣c)∈R^3

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:\left({a}\mid{b}\mid{c}\right)\in\mathbb{R}^{\mathrm{3}} \\ $$

Commented by MJS_new last updated on 09/Oct/20

let b=−a∧c=(1/(ab))=−(1/a^2 ) ⇒ (((a^2 +a+1)(a^2 −a+1)(a^2 −a+1))/a^3 )≤1 (1) ((a^6 −a^5 −2a^3 −a−1)/a^3 )≤0 but the numerator has got 2 real zeros a_1 ≈−.560769∧a_2 =−(1/a_1 )≈1.78326 ⇒ (1) is true for a≤a_1 ∨0<a≤a_2 and wrong for a_1 <a<0∨a>a_2

$$\mathrm{let}\:{b}=−{a}\wedge{c}=\frac{\mathrm{1}}{{ab}}=−\frac{\mathrm{1}}{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$$\frac{\left({a}^{\mathrm{2}} +{a}+\mathrm{1}\right)\left({a}^{\mathrm{2}} −{a}+\mathrm{1}\right)\left({a}^{\mathrm{2}} −{a}+\mathrm{1}\right)}{{a}^{\mathrm{3}} }\leqslant\mathrm{1}\:\left(\mathrm{1}\right) \\ $$$$\frac{{a}^{\mathrm{6}} −{a}^{\mathrm{5}} −\mathrm{2}{a}^{\mathrm{3}} −{a}−\mathrm{1}}{{a}^{\mathrm{3}} }\leqslant\mathrm{0} \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{numerator}\:\mathrm{has}\:\mathrm{got}\:\mathrm{2}\:\mathrm{real}\:\mathrm{zeros} \\ $$$${a}_{\mathrm{1}} \approx−.\mathrm{560769}\wedge{a}_{\mathrm{2}} =−\frac{\mathrm{1}}{{a}_{\mathrm{1}} }\approx\mathrm{1}.\mathrm{78326} \\ $$$$\Rightarrow\:\left(\mathrm{1}\right)\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:{a}\leqslant{a}_{\mathrm{1}} \vee\mathrm{0}<{a}\leqslant{a}_{\mathrm{2}} \:\mathrm{and} \\ $$$$\:\:\:\:\:\:\mathrm{wrong}\:\mathrm{for}\:{a}_{\mathrm{1}} <{a}<\mathrm{0}\vee{a}>{a}_{\mathrm{2}} \\ $$

Commented by 1549442205PVT last updated on 10/Oct/20

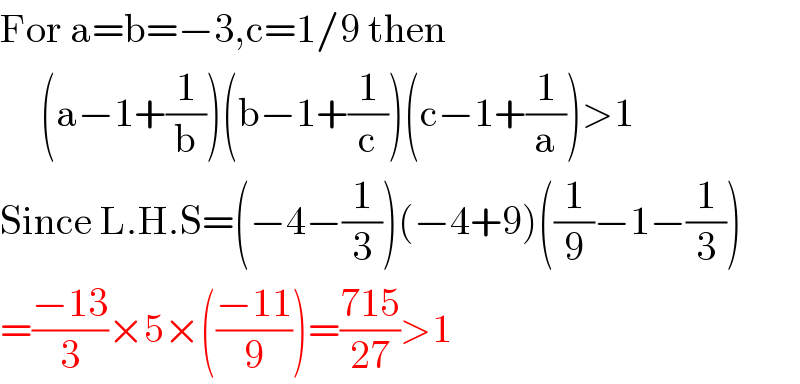
For a=b=−3,c=1/9 then (a−1+(1/b))(b−1+(1/c))(c−1+(1/a))>1 Since L.H.S=(−4−(1/3))(−4+9)((1/9)−1−(1/3)) =((−13)/3)×5×(((−11)/9))=((715)/(27))>1

$$\mathrm{For}\:\mathrm{a}=\mathrm{b}=−\mathrm{3},\mathrm{c}=\mathrm{1}/\mathrm{9}\:\mathrm{then} \\ $$$$\:\:\:\:\:\left(\mathrm{a}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{b}}\right)\left(\mathrm{b}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{c}}\right)\left(\mathrm{c}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{a}}\right)>\mathrm{1} \\ $$$$\mathrm{Since}\:\mathrm{L}.\mathrm{H}.\mathrm{S}=\left(−\mathrm{4}−\frac{\mathrm{1}}{\mathrm{3}}\right)\left(−\mathrm{4}+\mathrm{9}\right)\left(\frac{\mathrm{1}}{\mathrm{9}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{−\mathrm{13}}{\mathrm{3}}×\mathrm{5}×\left(\frac{−\mathrm{11}}{\mathrm{9}}\right)=\frac{\mathrm{715}}{\mathrm{27}}>\mathrm{1} \\ $$

Commented by Ar Brandon last updated on 13/Oct/20

OK Sir, thanks for your suggestions

Terms of Service

Privacy Policy

Contact: info@tinkutara.com