calculate ∫_(−∞) ^∞ (x^2 /((x^2 −x +1)^2 ))dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 117253 by mathmax by abdo last updated on 10/Oct/20

$calculate \int_{- \infty}^{\infty} \frac{x^{2}}{{(x^{2} - x + 1)}^{2}} dx$
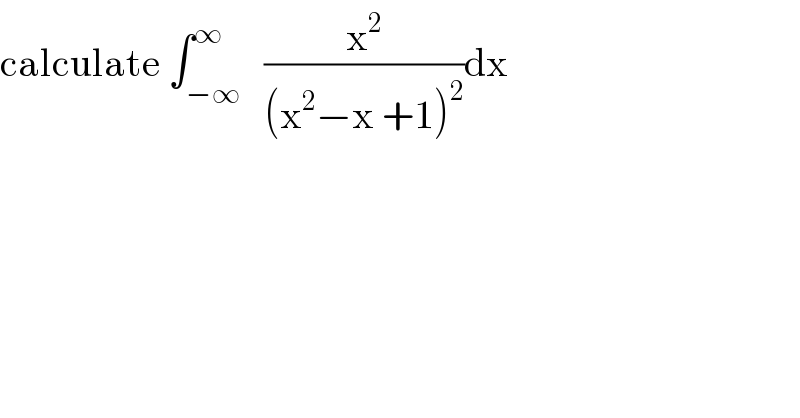
	Answered by mnjuly1970 last updated on 10/Oct/20
	$=∫_(−∞) ^( +∞) ((x^2 −x+1+x−1)/((x^2 −x+1)^2 ))dx =∫_(−∞) ^( +∞) (1/(x^2 −x+1))dx +(1/2)∫_(−∞) ^( +∞) ((2x−1−1)/((x^2 −x+1)^2 ))dx ({∫_(−∞) ^( +∞) (1/((x−(1/2))^2 +(((√3)/2))^2 ))dx}=k_1 ) −([(1/(2(x^2 −x+1)))]_(−∞) ^( ∞) =k_2 )−(1/2){∫_(−∞) ^( +∞) (1/((x^2 −x+1)^2 ))dx}=k_3 k_1 =((2π)/( (√3))) , k_2 =0 k_3 =∫_(−∞) ^( +∞) (1/((x^2 −x+1)^2 ))dx Λ(b)=∫_(−∞) ^( +∞) (1/(x^2 −x+b))dx=∫_(−∞) ^( +∞) (1/((x−(1/2))^2 +(((√(4b−1))/2))^2 )) =((2π)/( (√(4b−1)))) k_3 =−Λ^′ (b)∣_(b=1) =−2π(((−1)/2))(4)(4b−1)^(−(3/2)) ∣_(b=1) =(4π)(1/( 3(√3))) ∴ ∫_(−∞) ^( +∞) (x^2 /((x^2 −x+1)^2 ))dx=((2π)/( (√3)))−((2π)/(3(√3)))=((4π)/( 3(√3))) ....m.n.july.1970...$
	$= \int_{- \infty}^{+ \infty} \frac{x^{2} - x + 1 + x - 1}{{(x^{2} - x + 1)}^{2}} d x$ $= \int_{- \infty}^{+ \infty} \frac{1}{x^{2} - x + 1} d x + \frac{1}{2} \int_{- \infty}^{+ \infty} \frac{2 x - 1 - 1}{{(x^{2} - x + 1)}^{2}} d x$ $({\int_{- \infty}^{+ \infty} \frac{1}{{(x - \frac{1}{2})}^{2} + {(\frac{\sqrt{3}}{2})}^{2}} d x} = k_{1}) - ({[\frac{1}{2 (x^{2} - x + 1)}]}_{- \infty}^{\infty} = k_{2}) - \frac{1}{2} {\int_{- \infty}^{+ \infty} \frac{1}{{(x^{2} - x + 1)}^{2}} d x} = k_{3}$ $k_{1} = \frac{2 π}{\sqrt{3}}, k_{2} = 0$ $k_{3} = \int_{- \infty}^{+ \infty} \frac{1}{{(x^{2} - x + 1)}^{2}} d x$ $Λ (b) = \int_{- \infty}^{+ \infty} \frac{1}{x^{2} - x + b} d x = \int_{- \infty}^{+ \infty} \frac{1}{{(x - \frac{1}{2})}^{2} + {(\frac{\sqrt{4 b - 1}}{2})}^{2}}$ $= \frac{2 π}{\sqrt{4 b - 1}}$ $k_{3} = - Λ^{^{'}} (b) ∣_{b = 1} = - 2 π (\frac{- 1}{2}) (4) {(4 b - 1)}^{- \frac{3}{2}} ∣_{b = 1} = (4 π) \frac{1}{3 \sqrt{3}}$ $∴ \int_{- \infty}^{+ \infty} \frac{x^{2}}{{(x^{2} - x + 1)}^{2}} d x = \frac{2 π}{\sqrt{3}} - \frac{2 π}{3 \sqrt{3}} = \frac{4 π}{3 \sqrt{3}}$ $. . . . m . n . j u l y . 1970 . . .$
	Answered by Bird last updated on 10/Oct/20
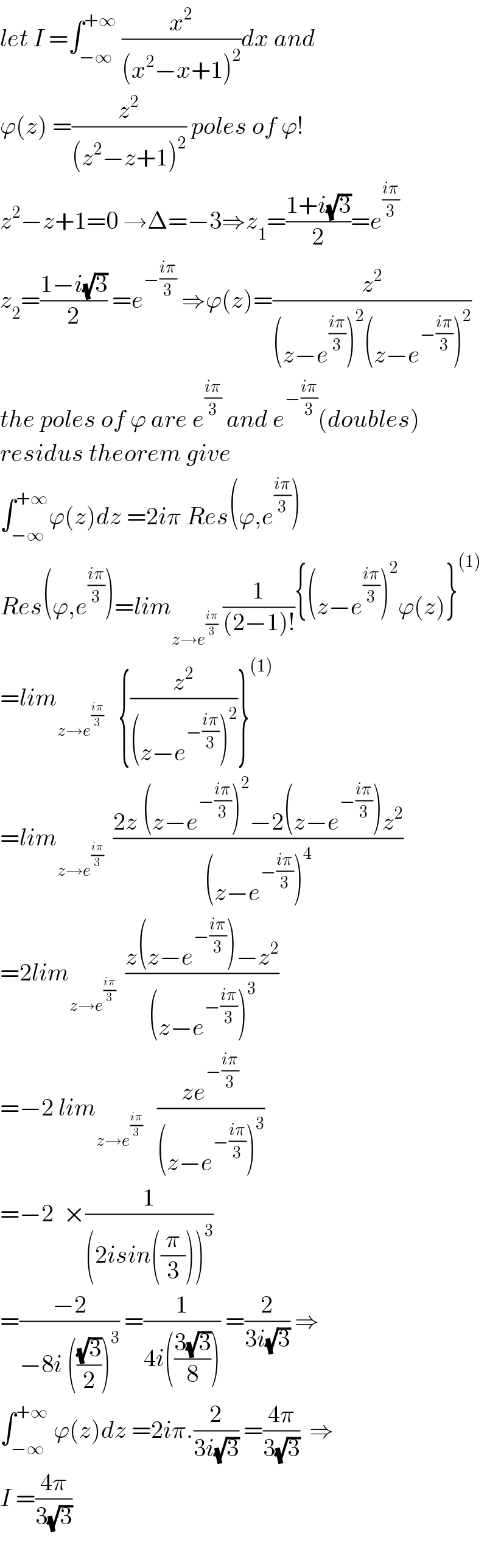
	$let I =∫_(−∞) ^(+∞) (x^2 /((x^2 −x+1)^2 ))dx and ϕ(z) =(z^2 /((z^2 −z+1)^2 )) poles of ϕ! z^2 −z+1=0 →Δ=−3⇒z_1 =((1+i(√3))/2)=e^((iπ)/3) z_2 =((1−i(√3))/2) =e^(−((iπ)/3)) ⇒ϕ(z)=(z^2 /((z−e^((iπ)/3) )^2 (z−e^(−((iπ)/3)) )^2 )) the poles of ϕ are e^((iπ)/3) and e^(−((iπ)/3)) (doubles) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,e^((iπ)/3) ) Res(ϕ,e^((iπ)/3) )=lim_(z→e^((iπ)/3) ) (1/((2−1)!)){(z−e^((iπ)/3) )^2 ϕ(z)}^((1)) =lim_(z→e^((iπ)/3) ) {(z^2 /((z−e^(−((iπ)/3)) )^2 ))}^((1)) =lim_(z→e^((iπ)/3) ) ((2z (z−e^(−((iπ)/3)) )^2 −2(z−e^(−((iπ)/3)) )z^2 )/((z−e^(−((iπ)/3)) )^4 )) =2lim_(z→e^((iπ)/3) ) ((z(z−e^(−((iπ)/3)) )−z^2 )/((z−e^(−((iπ)/3)) )^3 )) =−2 lim_(z→e^((iπ)/3) ) ((ze^(−((iπ)/3)) )/((z−e^(−((iπ)/3)) )^3 )) =−2 ×(1/((2isin((π/3)))^3 )) =((−2)/(−8i (((√3)/2))^3 )) =(1/(4i(((3(√3))/8)))) =(2/(3i(√3))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ.(2/(3i(√3))) =((4π)/(3(√3))) ⇒ I =((4π)/(3(√3)))$
	$l e t I = \int_{- \infty}^{+ \infty} \frac{x^{2}}{{(x^{2} - x + 1)}^{2}} d x a n d$ $φ (z) = \frac{z^{2}}{{(z^{2} - z + 1)}^{2}} p o l e s o f φ!$ $z^{2} - z + 1 = 0 \to Δ = - 3 \Rightarrow z_{1} = \frac{1 + i \sqrt{3}}{2} = e^{\frac{i π}{3}}$ $z_{2} = \frac{1 - i \sqrt{3}}{2} = e^{- \frac{i π}{3}} \Rightarrow φ (z) = \frac{z^{2}}{{(z - e^{\frac{i π}{3}})}^{2} {(z - e^{- \frac{i π}{3}})}^{2}}$ $t h e p o l e s o f φ a r e e^{\frac{i π}{3}} a n d e^{- \frac{i π}{3}} (d o u b l e s)$ $r e s i d u s t h e o r e m g i v e$ $\int_{- \infty}^{+ \infty} φ (z) d z = 2 i π R e s (φ, e^{\frac{i π}{3}})$ $R e s (φ, e^{\frac{i π}{3}}) = {l i m}_{z \to e^{\frac{i π}{3}}} \frac{1}{(2 - 1)!} {{(z - e^{\frac{i π}{3}})}^{2} φ (z)}^{(1)}$ $= {l i m}_{z \to e^{\frac{i π}{3}}} {\frac{z^{2}}{{(z - e^{- \frac{i π}{3}})}^{2}}}^{(1)}$ $= {l i m}_{z \to e^{\frac{i π}{3}}} \frac{2 z {(z - e^{- \frac{i π}{3}})}^{2} - 2 (z - e^{- \frac{i π}{3}}) z^{2}}{{(z - e^{- \frac{i π}{3}})}^{4}}$ $= 2 {l i m}_{z \to e^{\frac{i π}{3}}} \frac{z (z - e^{- \frac{i π}{3}}) - z^{2}}{{(z - e^{- \frac{i π}{3}})}^{3}}$ $= - 2 {l i m}_{z \to e^{\frac{i π}{3}}} \frac{{z e}^{- \frac{i π}{3}}}{{(z - e^{- \frac{i π}{3}})}^{3}}$ $= - 2 \times \frac{1}{{(2 i s i n (\frac{π}{3}))}^{3}}$ $= \frac{- 2}{- 8 i {(\frac{\sqrt{3}}{2})}^{3}} = \frac{1}{4 i (\frac{3 \sqrt{3}}{8})} = \frac{2}{3 i \sqrt{3}} \Rightarrow$ $\int_{- \infty}^{+ \infty} φ (z) d z = 2 i π . \frac{2}{3 i \sqrt{3}} = \frac{4 π}{3 \sqrt{3}} \Rightarrow$ $I = \frac{4 π}{3 \sqrt{3}}$
	Answered by 1549442205PVT last updated on 11/Oct/20
	$(x^2 /((x^2 −x +1)^2 ))≡ ((ax+b)/((x^2 −x +1)))+ ((cx^2 +dx+e)/(x^4 −2x^3 +3x^2 −2x+1)) ⇔x^2 ≡ax^5 +(c−2a)x^4 +(3a−2b−c+d)x^3 +(3b−2a+c−d+e)x^2 + +(a−2b+d−e)x+b+e ⇔ { ((a=0)),((c−2a=0)),((3a−2b−c+d=0)),((−2a+3b+c−d+e=1)),((a−2b+d−e=0)),((b+e=0)) :} ⇔ { ((a=0)),((b=2/3=d)),((e=−2/3)),((c=1/3)) :} Hence,∫_(−∞) ^∞ (x^2 /((x^2 −x +1)^2 ))dx =(2/3)∫_(−∞) ^(+∞) (dx/(x^2 −x+1))+(1/3)∫_(−∞) ^(+∞) ((x^2 +2x−2)/((x^2 −x+1)^2 ))dx Put F=∫((x^2 +2x−2)/((x^2 −x+1)^2 ))dx.We will find F in form:F(x)=((ax^2 +bx+c)/(x^2 −x+1))+C ⇔ ((x^2 +2x−2)/(2(x^2 −x +1)^2 ))≡F′(x)=(((ax^2 +bx+c)/(x^2 −x+1)))′ =(((2ax+b)(x^2 −x+1)−(ax^2 +bx+c)(2x−1))/((x^2 −x+1)^2 )) ={2ax^3 +(b−2a)x^2 +(2a−b)x+b −[2ax^3 +(2b−a)x^2 +(2c−b)x−c]}/(x^2 −x+1)^2 =(((−a−b)x^2 +(2a−2c)x+b+c)/((x^2 −x+1)^2 )) ⇔ { ((−a−b=1)),((2a−2c=2)),((b+c=−2)) :}⇔ { ((−2b−2c=4)),((b+c=−2)) :} ⇒b=−2−c a=−b−1=1+c ⇒F(x)=(((1+c)x^2 −(2+c)x+c)/(x^2 −x+1)) =((−x−1)/(x^2 −x+1))+c+1(1).We have (2/3)∫(dx/(x^2 −x+1))=(2/3)∫(dx/((x−(1/2))^2 +(((√3)/2))^2 )) =(2/3)×(2/( (√3)))tan^(−1) (((2x−1)/( (√3))))(2)(since ∫(dx/(x^2 +a^2 ))=tan^(−1) ((x/a))) From (1)(2) and (c+1) as a constant We get: I= ∫_(−∞) ^∞ (x^2 /((x^2 −x +1)^2 ))dx =[(4/(3(√3)))tan^(−1) (((2x−1)/( (√3))))−(1/3).((x+1)/(x^2 −x+1))]_(−∞) ^(+∞) =((4(√3))/9)×(π/2)×2=((4π(√3))/9)$
	$\frac{x^{2}}{{(x^{2} - x + 1)}^{2}} \equiv \frac{ax + b}{(x^{2} - x + 1)} + \frac{{cx}^{2} + dx + e}{x^{4} - {2 x}^{3} + {3 x}^{2} - 2 x + 1}$ $\Leftrightarrow x^{2} \equiv {ax}^{5} + (c - 2 a) x^{4} + (3 a - 2 b - c + d) x^{3}$ $+ (3 b - 2 a + c - d + e) x^{2} +$ $+ (a - 2 b + d - e) x + b + e$ $\Leftrightarrow {\begin{cases} a = 0 \\ c - 2 a = 0 \\ 3 a - 2 b - c + d = 0 \\ - 2 a + 3 b + c - d + e = 1 \\ a - 2 b + d - e = 0 \\ b + e = 0 \end{cases}$ $\Leftrightarrow {\begin{cases} a = 0 \\ b = 2 / 3 = d \\ e = - 2 / 3 \\ c = 1 / 3 \end{cases}$ $Hence, \int_{- \infty}^{\infty} \frac{x^{2}}{{(x^{2} - x + 1)}^{2}} dx$ $= \frac{2}{3} \int_{- \infty}^{+ \infty} \frac{dx}{x^{2} - x + 1} + \frac{1}{3} \int_{- \infty}^{+ \infty} \frac{x^{2} + 2 x - 2}{{(x^{2} - x + 1)}^{2}} dx$ $Put F = \int \frac{x^{2} + 2 x - 2}{{(x^{2} - x + 1)}^{2}} dx . We will find F$ $in form : F (x) = \frac{{ax}^{2} + bx + c}{x^{2} - x + 1} + C$ $\Leftrightarrow \frac{x^{2} + 2 x - 2}{2 {(x^{2} - x + 1)}^{2}} \equiv F^{'} (x) = {(\frac{{ax}^{2} + bx + c}{x^{2} - x + 1})}^{'}$ $= \frac{(2 ax + b) (x^{2} - x + 1) - ({ax}^{2} + bx + c) (2 x - 1)}{{(x^{2} - x + 1)}^{2}}$ $= {{2 ax}^{3} + (b - 2 a) x^{2} + (2 a - b) x + b$ $- [{2 ax}^{3} + (2 b - a) x^{2} + (2 c - b) x - c]} / {(x^{2} - x + 1)}^{2}$ $= \frac{(- a - b) x^{2} + (2 a - 2 c) x + b + c}{{(x^{2} - x + 1)}^{2}}$ $\Leftrightarrow {\begin{cases} - a - b = 1 \\ 2 a - 2 c = 2 \\ b + c = - 2 \end{cases} \Leftrightarrow {\begin{cases} - 2 b - 2 c = 4 \\ b + c = - 2 \end{cases}$ $\Rightarrow b = - 2 - c$ $a = - b - 1 = 1 + c$ $\Rightarrow F (x) = \frac{(1 + c) x^{2} - (2 + c) x + c}{x^{2} - x + 1}$ $= \frac{- x - 1}{x^{2} - x + 1} + c + 1 (1) . We have$ $\frac{2}{3} \int \frac{dx}{x^{2} - x + 1} = \frac{2}{3} \int \frac{dx}{{(x - \frac{1}{2})}^{2} + {(\frac{\sqrt{3}}{2})}^{2}}$ $= \frac{2}{3} \times \frac{2}{\sqrt{3}} \tan^{- 1} (\frac{2 x - 1}{\sqrt{3}}) (2) (since \int \frac{dx}{x^{2} + a^{2}} = \tan^{- 1} (\frac{x}{a}))$ $From (1) (2) and (c + 1) as a constant$ $We get : I = \int_{- \infty}^{\infty} \frac{x^{2}}{{(x^{2} - x + 1)}^{2}} dx$ $= {[\frac{4}{3 \sqrt{3}} \tan^{- 1} (\frac{2 x - 1}{\sqrt{3}}) - \frac{1}{3} . \frac{x + 1}{x^{2} - x + 1}]}_{- \infty}^{+ \infty}$ $= \frac{4 \sqrt{3}}{9} \times \frac{π}{2} \times 2 = \frac{4 π \sqrt{3}}{9}$
	Commented by 1549442205PVT last updated on 11/Oct/20

	$Thank Prof . You are welcome .$
	Commented by mathmax by abdo last updated on 11/Oct/20

	$thank you sir .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum