Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 117311 by eric last updated on 10/Oct/20

Answered by Dwaipayan Shikari last updated on 10/Oct/20

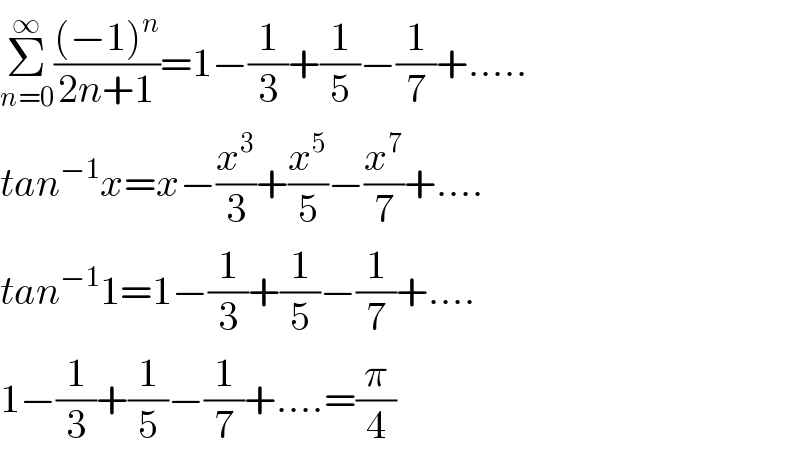
Σ_(n=0) ^∞ (((−1)^n )/(2n+1))=1−(1/3)+(1/5)−(1/7)+..... tan^(−1) x=x−(x^3 /3)+(x^5 /5)−(x^7 /7)+.... tan^(−1) 1=1−(1/3)+(1/5)−(1/7)+.... 1−(1/3)+(1/5)−(1/7)+....=(π/4)

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+..... \\ $$$${tan}^{−\mathrm{1}} {x}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−\frac{{x}^{\mathrm{7}} }{\mathrm{7}}+.... \\ $$$${tan}^{−\mathrm{1}} \mathrm{1}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+.... \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+....=\frac{\pi}{\mathrm{4}} \\ $$

Commented by TANMAY PANACEA last updated on 10/Oct/20

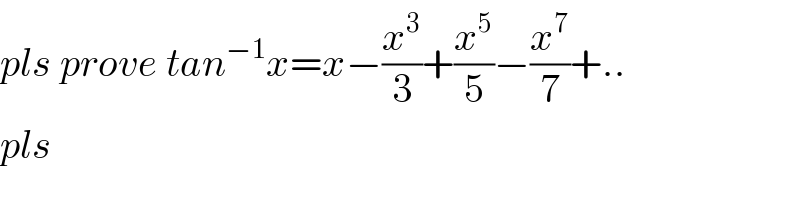
pls prove tan^(−1) x=x−(x^3 /3)+(x^5 /5)−(x^7 /7)+.. pls

$${pls}\:{prove}\:{tan}^{−\mathrm{1}} {x}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−\frac{{x}^{\mathrm{7}} }{\mathrm{7}}+.. \\ $$$${pls} \\ $$

Commented by Dwaipayan Shikari last updated on 10/Oct/20

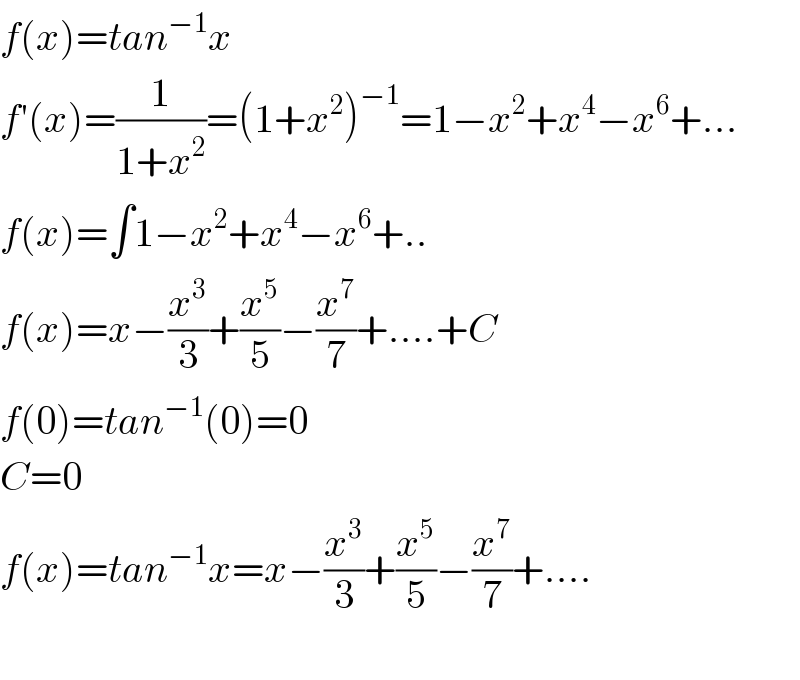
f(x)=tan^(−1) x f′(x)=(1/(1+x^2 ))=(1+x^2 )^(−1) =1−x^2 +x^4 −x^6 +... f(x)=∫1−x^2 +x^4 −x^6 +.. f(x)=x−(x^3 /3)+(x^5 /5)−(x^7 /7)+....+C f(0)=tan^(−1) (0)=0 C=0 f(x)=tan^(−1) x=x−(x^3 /3)+(x^5 /5)−(x^7 /7)+....

$${f}\left({x}\right)={tan}^{−\mathrm{1}} {x} \\ $$$${f}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\mathrm{1}} =\mathrm{1}−{x}^{\mathrm{2}} +{x}^{\mathrm{4}} −{x}^{\mathrm{6}} +... \\ $$$${f}\left({x}\right)=\int\mathrm{1}−{x}^{\mathrm{2}} +{x}^{\mathrm{4}} −{x}^{\mathrm{6}} +.. \\ $$$${f}\left({x}\right)={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−\frac{{x}^{\mathrm{7}} }{\mathrm{7}}+....+{C} \\ $$$${f}\left(\mathrm{0}\right)={tan}^{−\mathrm{1}} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$${C}=\mathrm{0} \\ $$$${f}\left({x}\right)={tan}^{−\mathrm{1}} {x}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−\frac{{x}^{\mathrm{7}} }{\mathrm{7}}+.... \\ $$$$ \\ $$

Commented by TANMAY PANACEA last updated on 10/Oct/20

excellent

$${excellent} \\ $$

Answered by mathmax by abdo last updated on 10/Oct/20

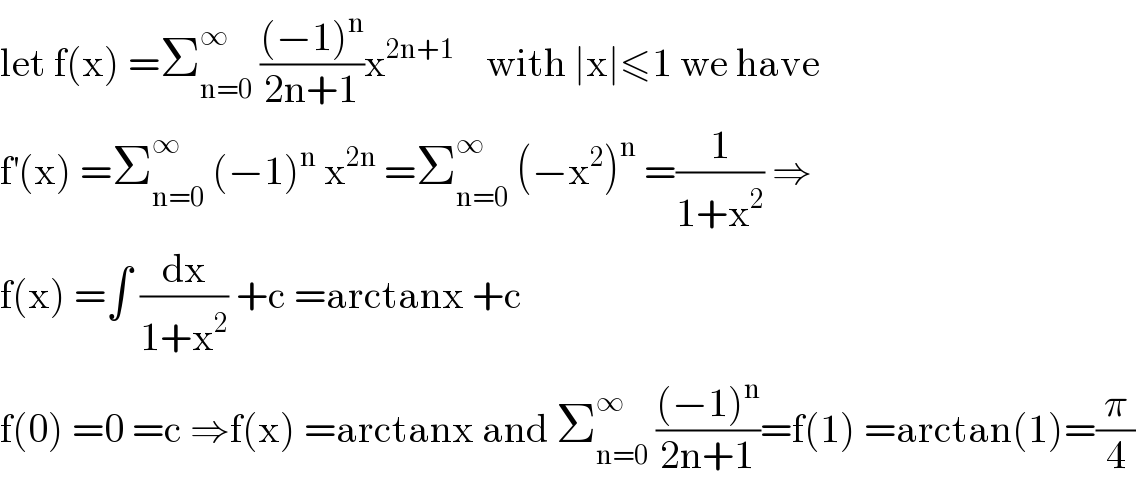
let f(x) =Σ_(n=0) ^∞ (((−1)^n )/(2n+1))x^(2n+1) with ∣x∣≤1 we have f^′ (x) =Σ_(n=0) ^∞ (−1)^n x^(2n) =Σ_(n=0) ^∞ (−x^2 )^n =(1/(1+x^2 )) ⇒ f(x) =∫ (dx/(1+x^2 )) +c =arctanx +c f(0) =0 =c ⇒f(x) =arctanx and Σ_(n=0) ^∞ (((−1)^n )/(2n+1))=f(1) =arctan(1)=(π/4)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \:\:\:\:\mathrm{with}\:\mid\mathrm{x}\mid\leqslant\mathrm{1}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} \:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\int\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:+\mathrm{c}\:=\mathrm{arctanx}\:+\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)\:=\mathrm{0}\:=\mathrm{c}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{arctanx}\:\mathrm{and}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}=\mathrm{f}\left(\mathrm{1}\right)\:=\mathrm{arctan}\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com