
Question Number 117329 by mnjuly1970 last updated on 12/Oct/20

$$\:\:\:\:\:\:\:\:\:{nice}\:\:{math} \\ $$$$\:\:{evaluate}:: \\ $$$$ \\ $$$$\:\:\:\: \\ $$$$\:\: \\ $$$$ \\ $$$$\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{arctan}\left({x}\right).{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}??? \\ $$$$\:\:\:\:\:\:\:\:\:{m}.{n}.\mathrm{1970} \\ $$$$ \\ $$
Answered by mindispower last updated on 11/Oct/20
![∫_0 ^1 ((arctan(t)ln(1−t))/(1+t^2 ))dt t=tg(x)⇔∫_0 ^(π/4) xln(1−tg(x))dx 1−tg(x)=(((√2)cos((π/4)+x))/(cos(x))) ⇔∫_0 ^(π/4) xln((√2))dx+∫_0 ^(π/4) xln(cos(x+(π/4)))dx−∫xln(cos(x))dx =(π^2 /(64))ln(2)+∫_0 ^(π/4) ((π/4)−x)ln(sin(x))dx−∫_0 ^(π/4) xln(cos(x))dx ∫_0 ^(π/4) ((π/4)−x)ln(sin(x))dx−∫_0 ^(π/4) xln(cos(x))dx =∫_0 ^(π/4) (π/4)ln(sin(x))dx−∫_0 ^(π/4) xln(((sin(2x))/2))dx fourier serie ln(sin(x))=−ln(2)−Σ_(n≥1) ((cos(2nx))/n);∀x∈[0,π] ∫ln(sin(x))dx=∫_0 ^(π/4) (−ln(2)−Σ_(n≥1) ((cos(2nx))/n)dx) =−((πln(2))/4)−Σ_(n≥1) [((sin(2nx))/(2n^2 ))]_0 ^(π/4) =−(π/4)ln(2)−(1/2)Σ_(n≥0) (((−1)^n )/((2n+1)^2 )) =−(π/4)(ln(2)+2G) ∫_0 ^(π/4) xln(((sin(2x))/2))dx=(1/4)∫_0 ^(π/2) yln(sin(y))dy−∫_0 ^(π/4) xln(2)dx =∫_0 ^(π/2) y(−ln(2)−Σ_(n≥1) ((cos(2ny))/n))dy−((π^2 ln(2))/(32)) =−(π^2 /(32))ln(2)−Σ_(n≥1) (1/(4n))∫_0 ^(π/2) ycos(2ny)dy−((π^2 ln(2))/(32)) =−((2π^2 ln(2))/(32))−Σ_(n≥1) (1/(8n^2 ))([[ysin(2ny)]_0 ^(π/2) −∫sin(2ny))dy) =−((4π^2 ln(2))/(64))−Σ_(n≥1) (1/(8n^3 ))[(−1)^n −1) =−((4π^2 ln(2))/(64))+Σ_(n≥1) (2/(4(2k+1)^3 ))=−((5π^2 ln(2))/(32))+(7/(64))ζ(3) (1/(64))(−4π^2 ln(2)+7ζ(3)) we get ((π^2 ln(2))/(64))+(π/4)(−(π/4)(ln(2)+2G))−(1/(64))(−4π^2 ln(2)+7ζ(3)) ((π^2 ln(2))/(64))+((Gπ)/2)−((7ζ(3))/(64))](Q117429.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arctan}\left({t}\right){ln}\left(\mathrm{1}−{t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${t}={tg}\left({x}\right)\Leftrightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {xln}\left(\mathrm{1}−{tg}\left({x}\right)\right){dx} \\ $$$$\mathrm{1}−{tg}\left({x}\right)=\frac{\sqrt{\mathrm{2}}{cos}\left(\frac{\pi}{\mathrm{4}}+{x}\right)}{{cos}\left({x}\right)} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {xln}\left(\sqrt{\mathrm{2}}\right){dx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {xln}\left({cos}\left({x}+\frac{\pi}{\mathrm{4}}\right)\right){dx}−\int{xln}\left({cos}\left({x}\right)\right){dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{64}}{ln}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\frac{\pi}{\mathrm{4}}−{x}\right){ln}\left({sin}\left({x}\right)\right){dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {xln}\left({cos}\left({x}\right)\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\frac{\pi}{\mathrm{4}}−{x}\right){ln}\left({sin}\left({x}\right)\right){dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {xln}\left({cos}\left({x}\right)\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\pi}{\mathrm{4}}{ln}\left({sin}\left({x}\right)\right){dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {xln}\left(\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right){dx} \\ $$$${fourier}\:{serie} \\ $$$${ln}\left({sin}\left({x}\right)\right)=−{ln}\left(\mathrm{2}\right)−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\mathrm{2}{nx}\right)}{{n}};\forall{x}\in\left[\mathrm{0},\pi\right] \\ $$$$\int{ln}\left({sin}\left({x}\right)\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(−{ln}\left(\mathrm{2}\right)−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\mathrm{2}{nx}\right)}{{n}}{dx}\right) \\ $$$$=−\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{4}}−\underset{{n}\geqslant\mathrm{1}} {\sum}\left[\frac{{sin}\left(\mathrm{2}{nx}\right)}{\mathrm{2}{n}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\frac{\pi}{\mathrm{4}}\left({ln}\left(\mathrm{2}\right)+\mathrm{2}{G}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {xln}\left(\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right){dx}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {yln}\left({sin}\left({y}\right)\right){dy}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {xln}\left(\mathrm{2}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {y}\left(−{ln}\left(\mathrm{2}\right)−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\mathrm{2}{ny}\right)}{{n}}\right){dy}−\frac{\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{32}} \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{32}}{ln}\left(\mathrm{2}\right)−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{4}{n}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ycos}\left(\mathrm{2}{ny}\right){dy}−\frac{\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{32}} \\ $$$$=−\frac{\mathrm{2}\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{32}}−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{8}{n}^{\mathrm{2}} }\left(\left[\left[{ysin}\left(\mathrm{2}{ny}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\int{sin}\left(\mathrm{2}{ny}\right)\right){dy}\right) \\ $$$$=−\frac{\mathrm{4}\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{64}}−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{8}{n}^{\mathrm{3}} }\left[\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}\right) \\ $$$$=−\frac{\mathrm{4}\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{64}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{2}}{\mathrm{4}\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{3}} }=−\frac{\mathrm{5}\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{32}}+\frac{\mathrm{7}}{\mathrm{64}}\zeta\left(\mathrm{3}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{64}}\left(−\mathrm{4}\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)+\mathrm{7}\zeta\left(\mathrm{3}\right)\right) \\ $$$${we}\:{get}\:\frac{\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{64}}+\frac{\pi}{\mathrm{4}}\left(−\frac{\pi}{\mathrm{4}}\left({ln}\left(\mathrm{2}\right)+\mathrm{2}{G}\right)\right)−\frac{\mathrm{1}}{\mathrm{64}}\left(−\mathrm{4}\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)+\mathrm{7}\zeta\left(\mathrm{3}\right)\right) \\ $$$$\frac{\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{64}}+\frac{{G}\pi}{\mathrm{2}}−\frac{\mathrm{7}\zeta\left(\mathrm{3}\right)}{\mathrm{64}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 11/Oct/20
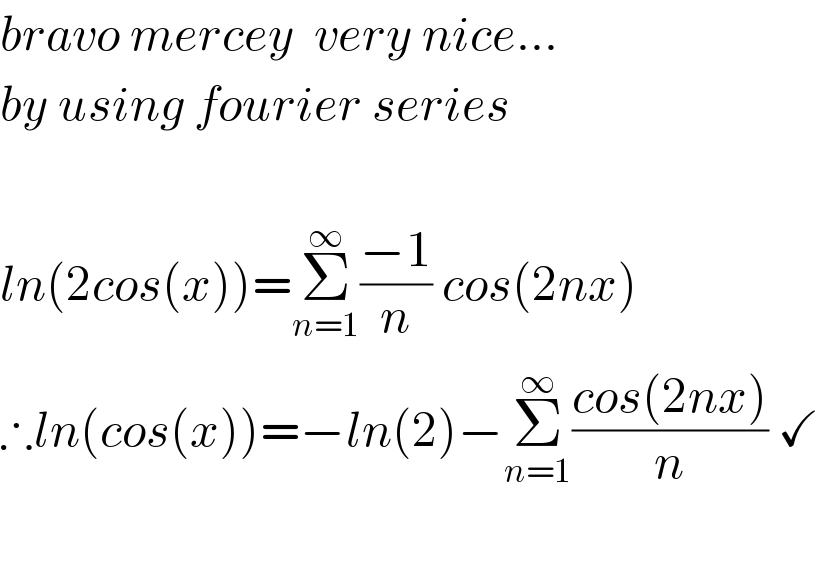
$${bravo}\:{mercey}\:\:{very}\:{nice}... \\ $$$${by}\:{using}\:{fourier}\:{series} \\ $$$$ \\ $$$${ln}\left(\mathrm{2}{cos}\left({x}\right)\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{−\mathrm{1}}{{n}}\:{cos}\left(\mathrm{2}{nx}\right)\: \\ $$$$\therefore{ln}\left({cos}\left({x}\right)\right)=−{ln}\left(\mathrm{2}\right)−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cos}\left(\mathrm{2}{nx}\right)}{{n}}\:\checkmark \\ $$$$ \\ $$
Commented by mindispower last updated on 11/Oct/20

$${withe}\:{pleasur} \\ $$
