
Question and Answers Forum
Question Number 117380 by mnjuly1970 last updated on 11/Oct/20
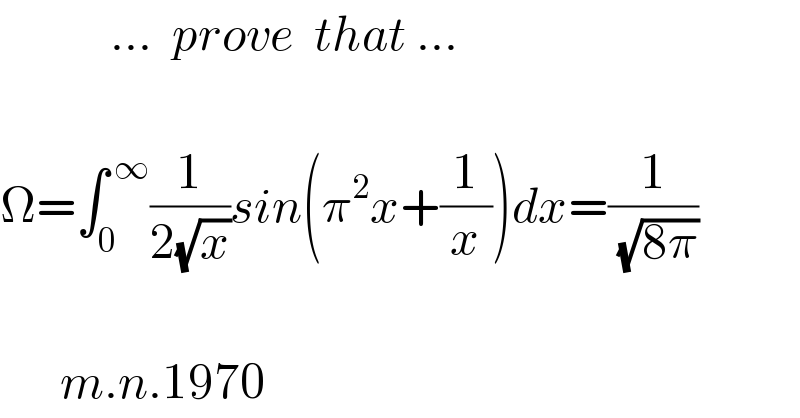
Commented by mindispower last updated on 11/Oct/20

Answered by mnjuly1970 last updated on 13/Oct/20
![solution:: Recall ::∫_0 ^( ∞) sin(z^2 )dz =^(..fresnel integral..) (√(π/8)) Ω =^(t=(√x)) ∫_0 ^( ∞) sin(π^2 t^2 +(1/t^2 ))dt πΩ=∫_0 ^( ∞) πsin(π^2 t^2 +(1/t^2 ))dt (i) πΩ =^(t=(1/(πu))) (1/π) ∫_(0 ) ^( ∞) πsin((1/u^2 )+π^2 u^2 )(du/u^2 ) πΩ=∫_0 ^( ∞) sin(π^2 u^2 +(1/u^2 ))(du/u^2 ) (ii) (i)+(ii) :: 2πΩ =∫_0 ^( ∞) (π+(1/x^2 ))sin[(πx−(1/x))^2 +2π]du 2πΩ=^(πx−(1/x)=y) ∫_(−∞) ^( ∞) sin(y^2 )dy 2πΩ =^(Recall ) 2 (√(π/8)) ⇒ Ω =(√(1/(8π))) ✓ ...♣M.N.july.1970♣... ♠peace be upon you♠](Q117725.png)
| ||
Question and Answers Forum | ||
Question Number 117380 by mnjuly1970 last updated on 11/Oct/20 | ||
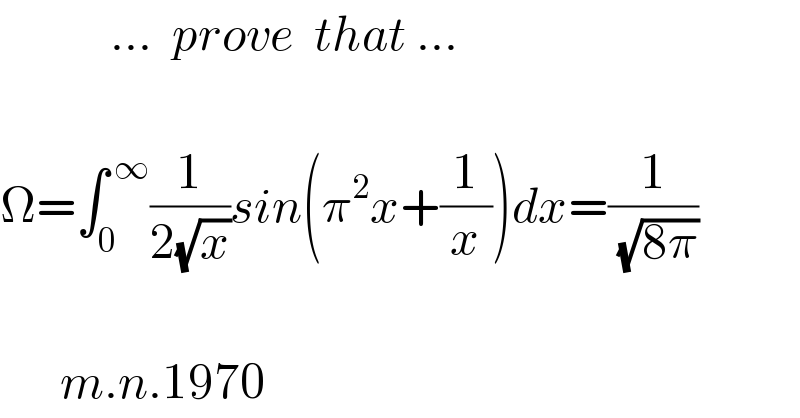 | ||
Commented by mindispower last updated on 11/Oct/20 | ||
 | ||
Answered by mnjuly1970 last updated on 13/Oct/20 | ||
![solution:: Recall ::∫_0 ^( ∞) sin(z^2 )dz =^(..fresnel integral..) (√(π/8)) Ω =^(t=(√x)) ∫_0 ^( ∞) sin(π^2 t^2 +(1/t^2 ))dt πΩ=∫_0 ^( ∞) πsin(π^2 t^2 +(1/t^2 ))dt (i) πΩ =^(t=(1/(πu))) (1/π) ∫_(0 ) ^( ∞) πsin((1/u^2 )+π^2 u^2 )(du/u^2 ) πΩ=∫_0 ^( ∞) sin(π^2 u^2 +(1/u^2 ))(du/u^2 ) (ii) (i)+(ii) :: 2πΩ =∫_0 ^( ∞) (π+(1/x^2 ))sin[(πx−(1/x))^2 +2π]du 2πΩ=^(πx−(1/x)=y) ∫_(−∞) ^( ∞) sin(y^2 )dy 2πΩ =^(Recall ) 2 (√(π/8)) ⇒ Ω =(√(1/(8π))) ✓ ...♣M.N.july.1970♣... ♠peace be upon you♠](Q117725.png) | ||
| ||