
Question and Answers Forum
Question Number 117403 by bemath last updated on 11/Oct/20
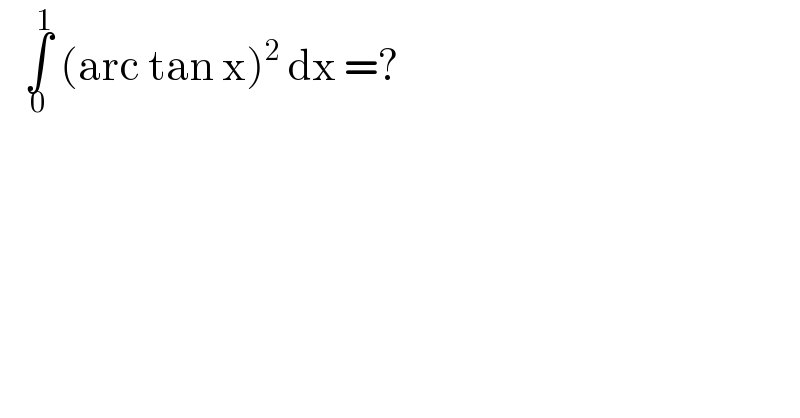
Commented by MJS_new last updated on 11/Oct/20
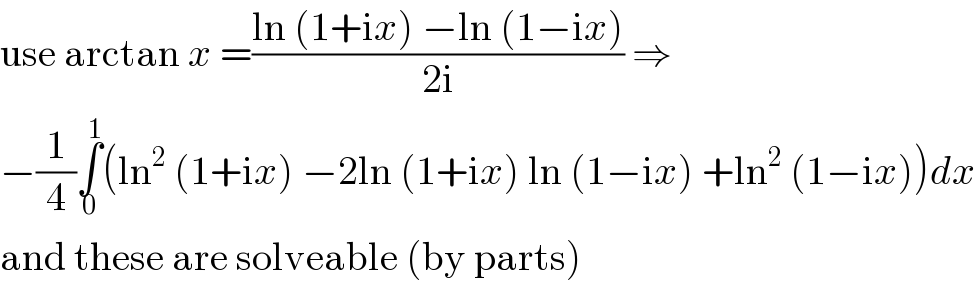
Answered by mindispower last updated on 11/Oct/20
![=[xarctan^2 (x)]_0 ^1 −∫_0 ^1 ((2x)/(1+x^2 ))arctan(x)dx =(π^2 /(16))−I let arctan(x)=t I=−∫_0 ^(π/4) ((2tg(t)t)/(1+tg^2 (t))).(1+tg^2 (t))dt =−2∫_0 ^(π/4) tg(t)tdt by part=−2([−tln(cost)]_0 ^(π/4) +∫_0 ^(π/4) ln(cos(t))dt =−(π/4)ln(2)−2∫_0 ^(π/4) ln(cos(t))dt one way too find it let a=∫_0 ^(π/4) ln(cos(t))dt =∫_0 ^(π/4) (1/2)ln(sin(t)cos(t).(1/(tg(t))))dt =∫_0 ^(π/4) ((ln(((sin(2t))/2)))/2)dt−(1/2)∫_0 ^(π/4) ln(tg(t))dt_(tg(t)=s) 2t=u⇒(1/4)∫_0 ^(π/2) ln(u)du−∫_0 ^(π/4) ln(2)du in first ∫_0 ^(π/4) ln(tg(t))dt=∫_0 ^1 ((ln(s))/(1+s^2 ))ds=Σ∫_0 ^1 (−1)^k s^(2k+1) ln(s)ds =−Σ(−1)^k .(1/((2k+1)^2 ))=−β(2) =−G ,G catalan constante knowing∫_0 ^(π/2) ln(sin(t))dt give us close forme 2nd use fourier serie of ln(cos(t))=−ln(2)−Σ_(n≥1) ((cos(2(2n−1)t))/(2n−1)) give use resulte imediatly withe Σ_(n≥1) (((−1)^(n−1) )/((2n−1)^2 )) =β(2)](Q117462.png)
| ||
Question and Answers Forum | ||
Question Number 117403 by bemath last updated on 11/Oct/20 | ||
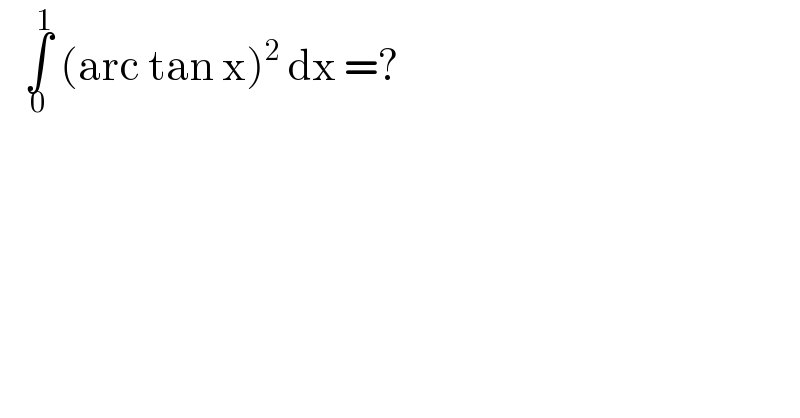 | ||
Commented by MJS_new last updated on 11/Oct/20 | ||
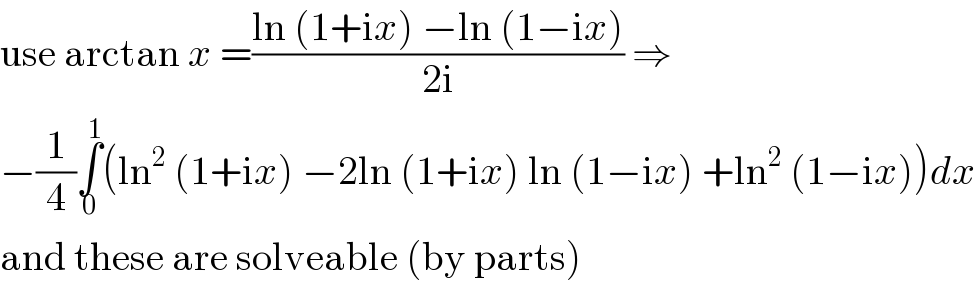 | ||
Answered by mindispower last updated on 11/Oct/20 | ||
![=[xarctan^2 (x)]_0 ^1 −∫_0 ^1 ((2x)/(1+x^2 ))arctan(x)dx =(π^2 /(16))−I let arctan(x)=t I=−∫_0 ^(π/4) ((2tg(t)t)/(1+tg^2 (t))).(1+tg^2 (t))dt =−2∫_0 ^(π/4) tg(t)tdt by part=−2([−tln(cost)]_0 ^(π/4) +∫_0 ^(π/4) ln(cos(t))dt =−(π/4)ln(2)−2∫_0 ^(π/4) ln(cos(t))dt one way too find it let a=∫_0 ^(π/4) ln(cos(t))dt =∫_0 ^(π/4) (1/2)ln(sin(t)cos(t).(1/(tg(t))))dt =∫_0 ^(π/4) ((ln(((sin(2t))/2)))/2)dt−(1/2)∫_0 ^(π/4) ln(tg(t))dt_(tg(t)=s) 2t=u⇒(1/4)∫_0 ^(π/2) ln(u)du−∫_0 ^(π/4) ln(2)du in first ∫_0 ^(π/4) ln(tg(t))dt=∫_0 ^1 ((ln(s))/(1+s^2 ))ds=Σ∫_0 ^1 (−1)^k s^(2k+1) ln(s)ds =−Σ(−1)^k .(1/((2k+1)^2 ))=−β(2) =−G ,G catalan constante knowing∫_0 ^(π/2) ln(sin(t))dt give us close forme 2nd use fourier serie of ln(cos(t))=−ln(2)−Σ_(n≥1) ((cos(2(2n−1)t))/(2n−1)) give use resulte imediatly withe Σ_(n≥1) (((−1)^(n−1) )/((2n−1)^2 )) =β(2)](Q117462.png) | ||
| ||