Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 11781 by tawa last updated on 31/Mar/17

sin(2θ) + 7cos(2θ) = 6 find θ

$$\mathrm{sin}\left(\mathrm{2}\theta\right)\:+\:\mathrm{7cos}\left(\mathrm{2}\theta\right)\:=\:\mathrm{6} \\ $$$$\mathrm{find}\:\theta \\ $$

Answered by sma3l2996 last updated on 31/Mar/17

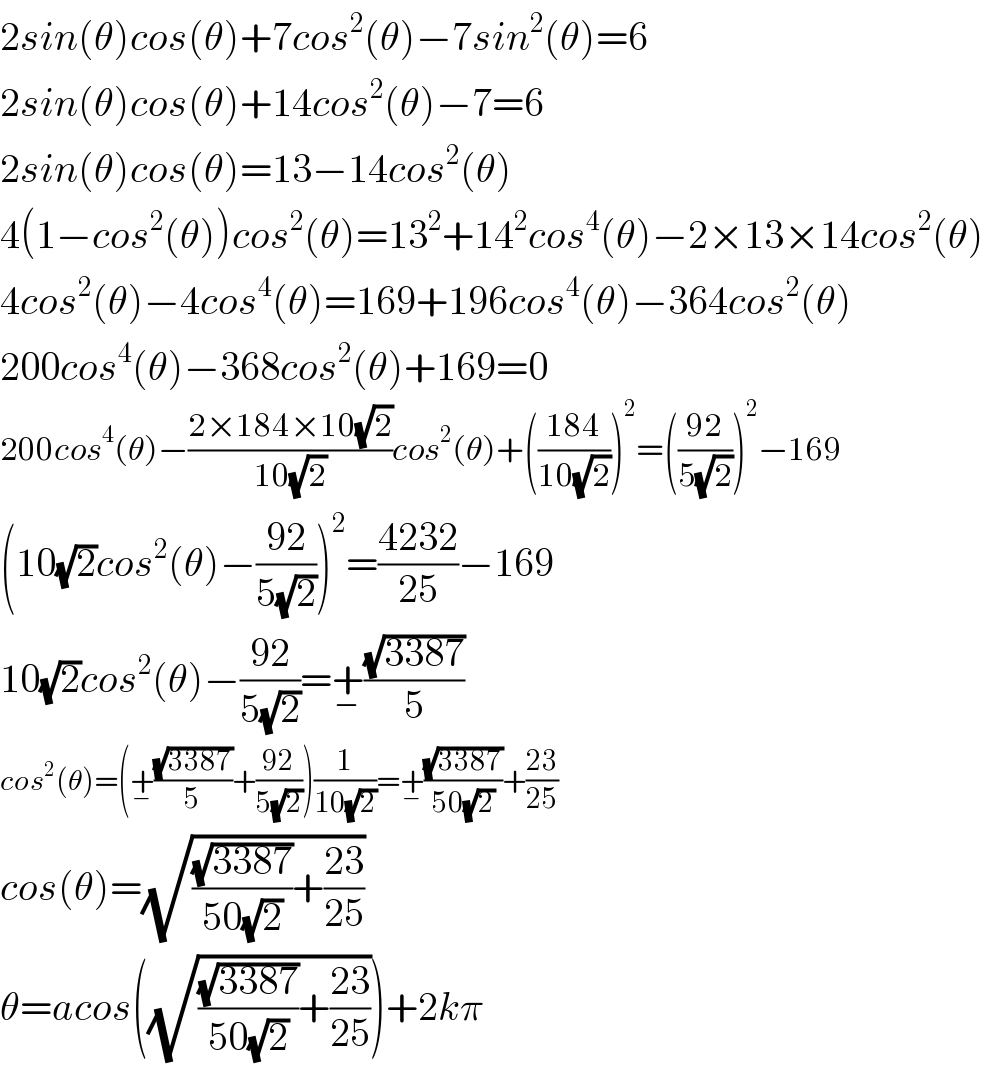
2sin(θ)cos(θ)+7cos^2 (θ)−7sin^2 (θ)=6 2sin(θ)cos(θ)+14cos^2 (θ)−7=6 2sin(θ)cos(θ)=13−14cos^2 (θ) 4(1−cos^2 (θ))cos^2 (θ)=13^2 +14^2 cos^4 (θ)−2×13×14cos^2 (θ) 4cos^2 (θ)−4cos^4 (θ)=169+196cos^4 (θ)−364cos^2 (θ) 200cos^4 (θ)−368cos^2 (θ)+169=0 200cos^4 (θ)−((2×184×10(√2))/(10(√2)))cos^2 (θ)+(((184)/(10(√2))))^2 =(((92)/(5(√2))))^2 −169 (10(√2)cos^2 (θ)−((92)/(5(√2))))^2 =((4232)/(25))−169 10(√2)cos^2 (θ)−((92)/(5(√2)))=+_− ((√(3387))/5) cos^2 (θ)=(+_− ((√(3387))/5)+((92)/(5(√2))))(1/(10(√2)))=+_− ((√(3387))/(50(√2)))+((23)/(25)) cos(θ)=(√(((√(3387))/(50(√2)))+((23)/(25)))) θ=acos((√(((√(3387))/(50(√2)))+((23)/(25)))))+2kπ

$$\mathrm{2}{sin}\left(\theta\right){cos}\left(\theta\right)+\mathrm{7}{cos}^{\mathrm{2}} \left(\theta\right)−\mathrm{7}{sin}^{\mathrm{2}} \left(\theta\right)=\mathrm{6} \\ $$$$\mathrm{2}{sin}\left(\theta\right){cos}\left(\theta\right)+\mathrm{14}{cos}^{\mathrm{2}} \left(\theta\right)−\mathrm{7}=\mathrm{6} \\ $$$$\mathrm{2}{sin}\left(\theta\right){cos}\left(\theta\right)=\mathrm{13}−\mathrm{14}{cos}^{\mathrm{2}} \left(\theta\right) \\ $$$$\mathrm{4}\left(\mathrm{1}−{cos}^{\mathrm{2}} \left(\theta\right)\right){cos}^{\mathrm{2}} \left(\theta\right)=\mathrm{13}^{\mathrm{2}} +\mathrm{14}^{\mathrm{2}} {cos}^{\mathrm{4}} \left(\theta\right)−\mathrm{2}×\mathrm{13}×\mathrm{14}{cos}^{\mathrm{2}} \left(\theta\right) \\ $$$$\mathrm{4}{cos}^{\mathrm{2}} \left(\theta\right)−\mathrm{4}{cos}^{\mathrm{4}} \left(\theta\right)=\mathrm{169}+\mathrm{196}{cos}^{\mathrm{4}} \left(\theta\right)−\mathrm{364}{cos}^{\mathrm{2}} \left(\theta\right) \\ $$$$\mathrm{200}{cos}^{\mathrm{4}} \left(\theta\right)−\mathrm{368}{cos}^{\mathrm{2}} \left(\theta\right)+\mathrm{169}=\mathrm{0} \\ $$$$\mathrm{200}{cos}^{\mathrm{4}} \left(\theta\right)−\frac{\mathrm{2}×\mathrm{184}×\mathrm{10}\sqrt{\mathrm{2}}}{\mathrm{10}\sqrt{\mathrm{2}}}{cos}^{\mathrm{2}} \left(\theta\right)+\left(\frac{\mathrm{184}}{\mathrm{10}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{92}}{\mathrm{5}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\mathrm{169} \\ $$$$\left(\mathrm{10}\sqrt{\mathrm{2}}{cos}^{\mathrm{2}} \left(\theta\right)−\frac{\mathrm{92}}{\mathrm{5}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} =\frac{\mathrm{4232}}{\mathrm{25}}−\mathrm{169} \\ $$$$\mathrm{10}\sqrt{\mathrm{2}}{cos}^{\mathrm{2}} \left(\theta\right)−\frac{\mathrm{92}}{\mathrm{5}\sqrt{\mathrm{2}}}=\underset{−} {+}\frac{\sqrt{\mathrm{3387}}}{\mathrm{5}}\: \\ $$$${cos}^{\mathrm{2}} \left(\theta\right)=\left(\underset{−} {+}\frac{\sqrt{\mathrm{3387}}}{\mathrm{5}}+\frac{\mathrm{92}}{\mathrm{5}\sqrt{\mathrm{2}}}\right)\frac{\mathrm{1}}{\mathrm{10}\sqrt{\mathrm{2}}}=\underset{−} {+}\frac{\sqrt{\mathrm{3387}}}{\mathrm{50}\sqrt{\mathrm{2}}}+\frac{\mathrm{23}}{\mathrm{25}} \\ $$$${cos}\left(\theta\right)=\sqrt{\frac{\sqrt{\mathrm{3387}}}{\mathrm{50}\sqrt{\mathrm{2}}}+\frac{\mathrm{23}}{\mathrm{25}}} \\ $$$$\theta={acos}\left(\sqrt{\frac{\sqrt{\mathrm{3387}}}{\mathrm{50}\sqrt{\mathrm{2}}}+\frac{\mathrm{23}}{\mathrm{25}}}\right)+\mathrm{2}{k}\pi \\ $$

Commented by tawa last updated on 31/Mar/17

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by sandy_suhendra last updated on 31/Mar/17

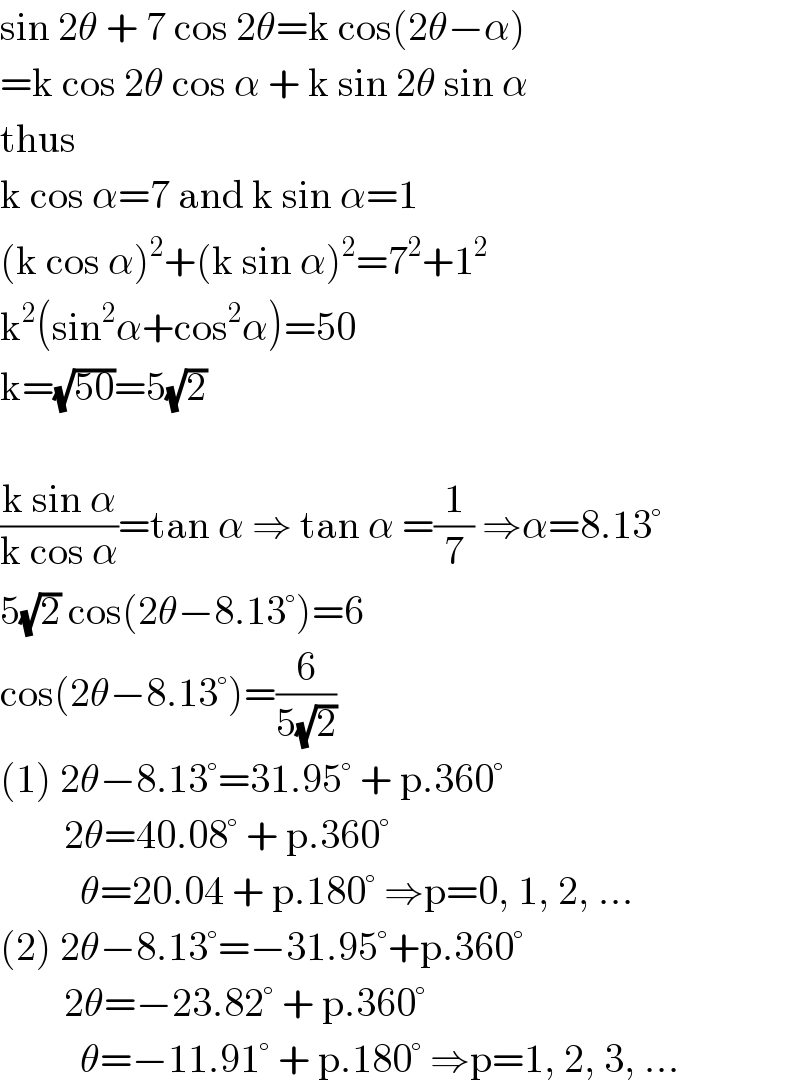
sin 2θ + 7 cos 2θ=k cos(2θ−α) =k cos 2θ cos α + k sin 2θ sin α thus k cos α=7 and k sin α=1 (k cos α)^2 +(k sin α)^2 =7^2 +1^2 k^2 (sin^2 α+cos^2 α)=50 k=(√(50))=5(√2) ((k sin α)/(k cos α))=tan α ⇒ tan α =(1/7) ⇒α=8.13° 5(√2) cos(2θ−8.13°)=6 cos(2θ−8.13°)=(6/(5(√2))) (1) 2θ−8.13°=31.95° + p.360° 2θ=40.08° + p.360° θ=20.04 + p.180° ⇒p=0, 1, 2, ... (2) 2θ−8.13°=−31.95°+p.360° 2θ=−23.82° + p.360° θ=−11.91° + p.180° ⇒p=1, 2, 3, ...

$$\mathrm{sin}\:\mathrm{2}\theta\:+\:\mathrm{7}\:\mathrm{cos}\:\mathrm{2}\theta=\mathrm{k}\:\mathrm{cos}\left(\mathrm{2}\theta−\alpha\right) \\ $$$$=\mathrm{k}\:\mathrm{cos}\:\mathrm{2}\theta\:\mathrm{cos}\:\alpha\:+\:\mathrm{k}\:\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{sin}\:\alpha \\ $$$$\mathrm{thus} \\ $$$$\mathrm{k}\:\mathrm{cos}\:\alpha=\mathrm{7}\:\mathrm{and}\:\mathrm{k}\:\mathrm{sin}\:\alpha=\mathrm{1} \\ $$$$\left(\mathrm{k}\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +\left(\mathrm{k}\:\mathrm{sin}\:\alpha\right)^{\mathrm{2}} =\mathrm{7}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} \\ $$$$\mathrm{k}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \alpha+\mathrm{cos}^{\mathrm{2}} \alpha\right)=\mathrm{50} \\ $$$$\mathrm{k}=\sqrt{\mathrm{50}}=\mathrm{5}\sqrt{\mathrm{2}} \\ $$$$ \\ $$$$\frac{\mathrm{k}\:\mathrm{sin}\:\alpha}{\mathrm{k}\:\mathrm{cos}\:\alpha}=\mathrm{tan}\:\alpha\:\Rightarrow\:\mathrm{tan}\:\alpha\:=\frac{\mathrm{1}}{\mathrm{7}}\:\Rightarrow\alpha=\mathrm{8}.\mathrm{13}°\:\:\:\:\: \\ $$$$\mathrm{5}\sqrt{\mathrm{2}}\:\mathrm{cos}\left(\mathrm{2}\theta−\mathrm{8}.\mathrm{13}°\right)=\mathrm{6} \\ $$$$\mathrm{cos}\left(\mathrm{2}\theta−\mathrm{8}.\mathrm{13}°\right)=\frac{\mathrm{6}}{\mathrm{5}\sqrt{\mathrm{2}}} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}\theta−\mathrm{8}.\mathrm{13}°=\mathrm{31}.\mathrm{95}°\:+\:\mathrm{p}.\mathrm{360}° \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}\theta=\mathrm{40}.\mathrm{08}°\:+\:\mathrm{p}.\mathrm{360}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\theta=\mathrm{20}.\mathrm{04}\:+\:\mathrm{p}.\mathrm{180}°\:\Rightarrow\mathrm{p}=\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:...\:\:\:\:\: \\ $$$$\left(\mathrm{2}\right)\:\mathrm{2}\theta−\mathrm{8}.\mathrm{13}°=−\mathrm{31}.\mathrm{95}°+\mathrm{p}.\mathrm{360}° \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}\theta=−\mathrm{23}.\mathrm{82}°\:+\:\mathrm{p}.\mathrm{360}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\theta=−\mathrm{11}.\mathrm{91}°\:+\:\mathrm{p}.\mathrm{180}°\:\Rightarrow\mathrm{p}=\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:...\:\:\:\:\: \\ $$

Commented by tawa last updated on 31/Mar/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Answered by ajfour last updated on 31/Mar/17

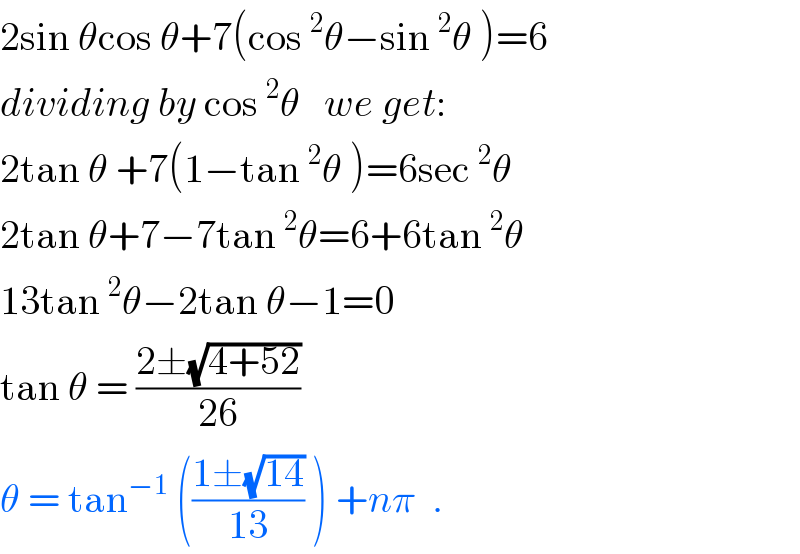
2sin θcos θ+7(cos^2 θ−sin^2 θ )=6 dividing by cos^2 θ we get: 2tan θ +7(1−tan^2 θ )=6sec^2 θ 2tan θ+7−7tan^2 θ=6+6tan^2 θ 13tan^2 θ−2tan θ−1=0 tan θ = ((2±(√(4+52)))/(26)) θ = tan^(−1) (((1±(√(14)))/(13)) ) +nπ .

$$\mathrm{2sin}\:\theta\mathrm{cos}\:\theta+\mathrm{7}\left(\mathrm{cos}\:^{\mathrm{2}} \theta−\mathrm{sin}\:^{\mathrm{2}} \theta\:\right)=\mathrm{6} \\ $$$${dividing}\:{by}\:\mathrm{cos}\:^{\mathrm{2}} \theta\:\:\:{we}\:{get}: \\ $$$$\mathrm{2tan}\:\theta\:+\mathrm{7}\left(\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \theta\:\right)=\mathrm{6sec}\:^{\mathrm{2}} \theta \\ $$$$\mathrm{2tan}\:\theta+\mathrm{7}−\mathrm{7tan}\:^{\mathrm{2}} \theta=\mathrm{6}+\mathrm{6tan}\:^{\mathrm{2}} \theta \\ $$$$\mathrm{13tan}\:^{\mathrm{2}} \theta−\mathrm{2tan}\:\theta−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{tan}\:\theta\:=\:\frac{\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{52}}}{\mathrm{26}} \\ $$$$\theta\:=\:\mathrm{tan}^{−\mathrm{1}} \:\left(\frac{\mathrm{1}\pm\sqrt{\mathrm{14}}}{\mathrm{13}}\:\right)\:+{n}\pi\:\:. \\ $$

Commented by tawa last updated on 31/Mar/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com