
Question and Answers Forum
Question Number 117944 by bemath last updated on 14/Oct/20
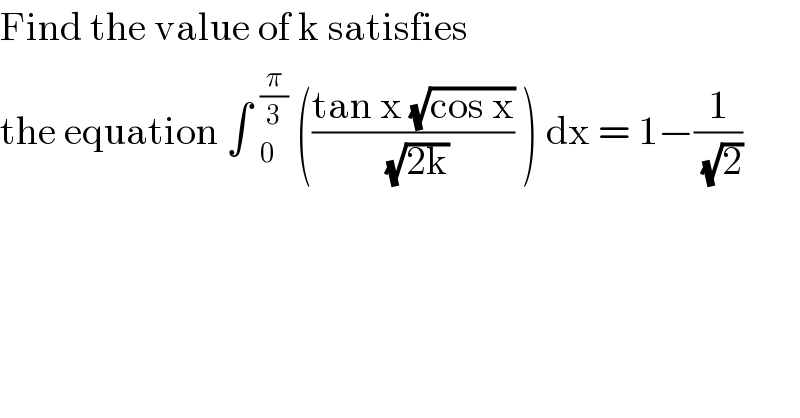
Answered by john santu last updated on 14/Oct/20
![∫ _0^(π/3) (((sin x (√(cos x)))/( (√(2k)) cos x)) ) dx = (((√2)−1)/( (√2))) ⇒(1/( (√k))) ∫_0 ^(π/3) ((sin x)/( (√(cos x)))) dx = (√2)−1 ⇒(1/( (√k) )) ∫_0 ^(π/3) ((d(cos x))/( (√(cos x)))) = 1−(√2) ⇒[ ((2 (√(cos x)))/( (√k))) ]_0 ^(π/3) = 1−(√2) ⇒(((2/( (√2)))−2)/( (√k))) = 1−(√2) ; k = ((((√2)−2)/(1−(√2))))^2 ⇒k = ((((√2)(1−(√2)))/(1−(√2))))^2 = 2](Q117950.png)
Answered by Dwaipayan Shikari last updated on 14/Oct/20
![(1/( (√(2k))))∫_0 ^(π/3) ((sinx)/( (√(cosx))))dx=−(1/( (√(2k))))∫_1 ^(1/2) (dt/( (√t)))=(√(2/k)) [(√t)]_(1/2) ^1 (√(2/k))(1−(1/( (√2))))=1−(1/( (√2))) (2/k)=1 k=2](Q117951.png)
Answered by 1549442205PVT last updated on 14/Oct/20
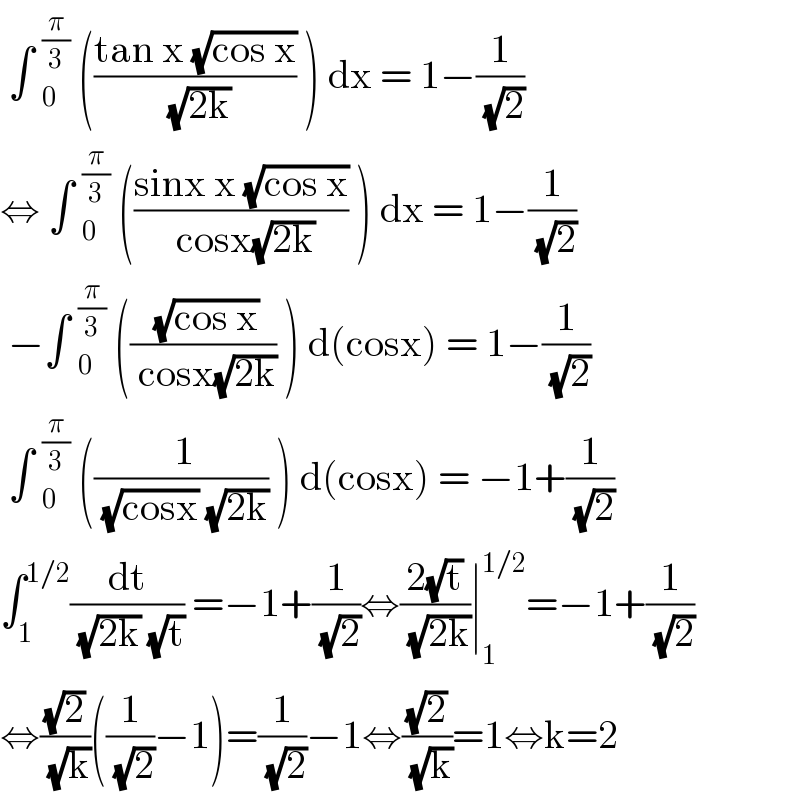
| ||
Question and Answers Forum | ||
Question Number 117944 by bemath last updated on 14/Oct/20 | ||
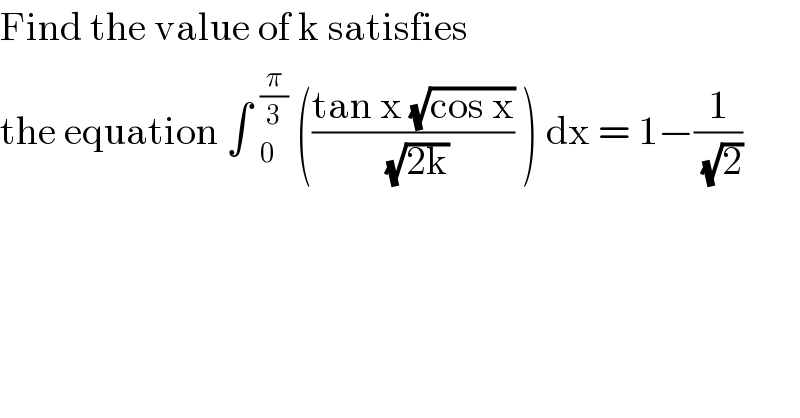 | ||
Answered by john santu last updated on 14/Oct/20 | ||
![∫ _0^(π/3) (((sin x (√(cos x)))/( (√(2k)) cos x)) ) dx = (((√2)−1)/( (√2))) ⇒(1/( (√k))) ∫_0 ^(π/3) ((sin x)/( (√(cos x)))) dx = (√2)−1 ⇒(1/( (√k) )) ∫_0 ^(π/3) ((d(cos x))/( (√(cos x)))) = 1−(√2) ⇒[ ((2 (√(cos x)))/( (√k))) ]_0 ^(π/3) = 1−(√2) ⇒(((2/( (√2)))−2)/( (√k))) = 1−(√2) ; k = ((((√2)−2)/(1−(√2))))^2 ⇒k = ((((√2)(1−(√2)))/(1−(√2))))^2 = 2](Q117950.png) | ||
| ||
Answered by Dwaipayan Shikari last updated on 14/Oct/20 | ||
![(1/( (√(2k))))∫_0 ^(π/3) ((sinx)/( (√(cosx))))dx=−(1/( (√(2k))))∫_1 ^(1/2) (dt/( (√t)))=(√(2/k)) [(√t)]_(1/2) ^1 (√(2/k))(1−(1/( (√2))))=1−(1/( (√2))) (2/k)=1 k=2](Q117951.png) | ||
| ||
Answered by 1549442205PVT last updated on 14/Oct/20 | ||
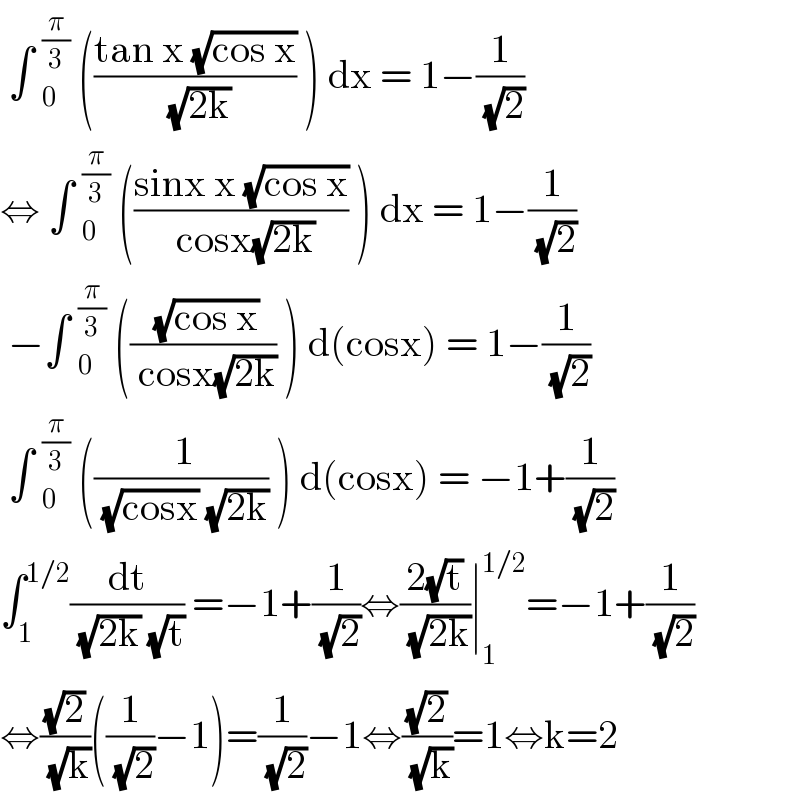 | ||
| ||