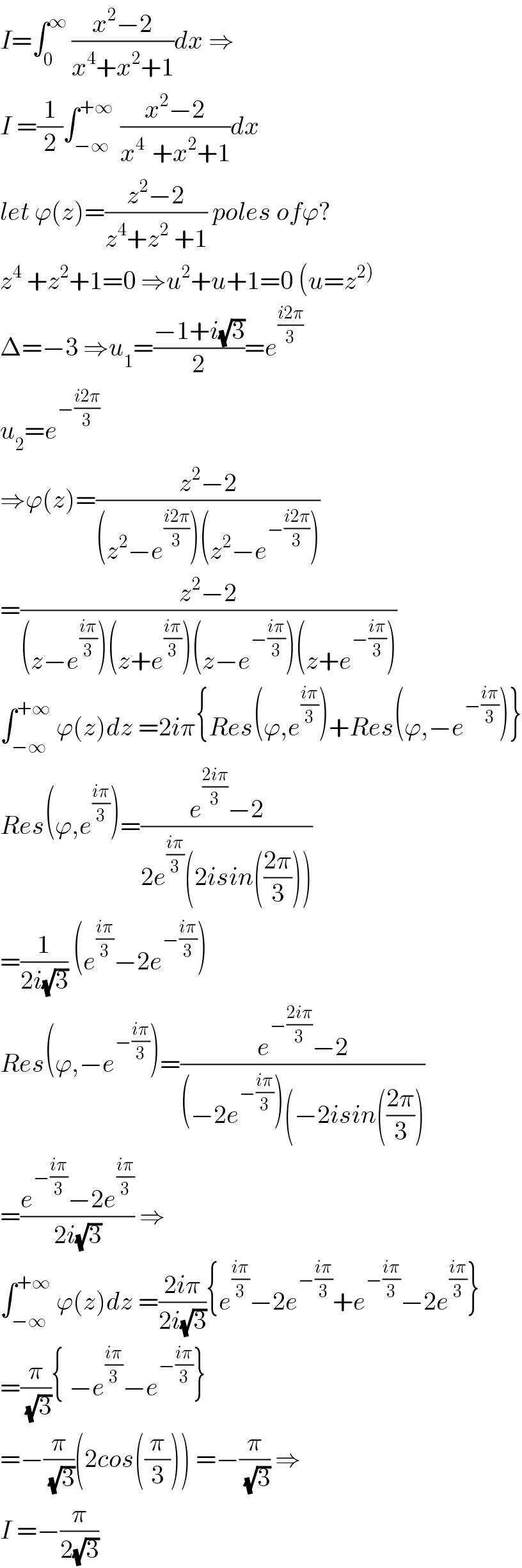Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 118030 by mathmax by abdo last updated on 14/Oct/20

$$\mathrm{find}{\int }_0^{\mathrm{\infty }}\frac{{\mathrm{x}}^2-2}{{\mathrm{x}}^4+{\mathrm{x}}^2+1}\mathrm{dx}$$

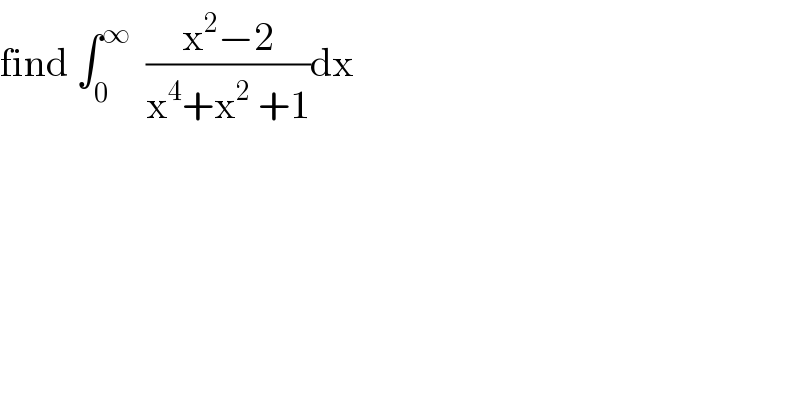
Commented by Ar Brandon last updated on 14/Oct/20

$$\mathrm{My}\mathrm{idea}\mathrm{is}\mathrm{often}\mathrm{to}\mathrm{express}\mathrm{the}\mathrm{terms}\mathrm{in}\mathrm{the}$$$$\mathrm{numerator}\mathrm{like}\mathrm{those}\mathrm{of}\mathrm{the}\mathrm{square}-\mathrm{roots}\mathrm{of}\mathrm{the}\mathrm{first}$$$$\mathrm{and}\mathrm{last}\mathrm{terms}\mathrm{in}\mathrm{the}\mathrm{denominator}.\mathrm{Just}\mathrm{like}\mathrm{in}\mathrm{Q}117446$$$${\mathrm{x}}^2-2=({\mathrm{x}}^2-1)-1$$$$=({\mathrm{x}}^2-1)-\frac{({\mathrm{x}}^2+1)-({\mathrm{x}}^2-1)}{2}$$$$=\frac{3}{2}({\mathrm{x}}^2-1)-\frac{1}{2}({\mathrm{x}}^2+1)$$

Answered by Ar Brandon last updated on 14/Oct/20

$$\mathcal{I}={\int }_0^{\mathrm{\infty }}\frac{{\mathrm{x}}^2-2}{{\mathrm{x}}^4+{\mathrm{x}}^2+1}\mathrm{dx}=\frac{3}{2}{\int }_0^{\mathrm{\infty }}\frac{({\mathrm{x}}^2-1)}{{\mathrm{x}}^4+{\mathrm{x}}^2+1}\mathrm{dx}-\frac{1}{2}{\int }_0^{\mathrm{\infty }}\frac{({\mathrm{x}}^2+1)}{{\mathrm{x}}^4+{\mathrm{x}}^2+1}\mathrm{dx}$$$$=\frac{3}{2}{\int }_0^{\mathrm{\infty }}\frac{1-\frac{1}{{\mathrm{x}}^2}}{{\mathrm{x}}^2+1+\frac{1}{{\mathrm{x}}^2}}\mathrm{dx}-\frac{1}{2}{\int }_0^{\mathrm{\infty }}\frac{1+\frac{1}{{\mathrm{x}}^2}}{{\mathrm{x}}^2+1+\frac{1}{{\mathrm{x}}^2}}\mathrm{dx}$$$$=\frac{3}{2}{\int }_0^{\mathrm{\infty }}\frac{1-\frac{1}{{\mathrm{x}}^2}}{{(\mathrm{x}+\frac{1}{\mathrm{x}})}^2-1}\mathrm{dx}-\frac{1}{2}{\int }_0^{\mathrm{\infty }}\frac{1+\frac{1}{{\mathrm{x}}^2}}{{(\mathrm{x}-\frac{1}{\mathrm{x}})}^2+3}\mathrm{dx}$$$$=\frac{3}{2}{\int }_{+\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{du}}{{\mathrm{u}}^2-1}-\frac{1}{2}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{dv}}{{\mathrm{v}}^2+3}=-\frac{1}{2}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{dv}}{{\mathrm{v}}^2+3}$$$$=-{\left[\frac{1}{2\sqrt{3}}\mathrm{Arctan}\left(\frac{\mathrm{v}}{\sqrt{3}}\right)\right]}_{-\mathrm{\infty }}^{+\mathrm{\infty }}=-\frac{1}{2\sqrt{3}}(\frac{\pi }{2}+\frac{\pi }{2})=-\frac{\pi }{2\sqrt{3}}$$

Commented by Lordose last updated on 14/Oct/20

$$\mathrm{Excellente}$$

Commented by Ar Brandon last updated on 14/Oct/20

Merci. J'suis ravi !

Commented by Ar Brandon last updated on 14/Oct/20

S'il vous plaît, pouvez-vous jeter un oeil sur la Question 117972 ? Il semble avoir un problème avec votre réponse.

Commented by Lordose last updated on 15/Oct/20

Je pense que la meilleure façon de résoudre la question 117927 est de dessiner les cartes.��

Commented by Ar Brandon last updated on 15/Oct/20

Je n'arrive pas à le faire malheureusement

Commented by Lordose last updated on 15/Oct/20

D'accord. Je suis un peu occupé maintenant. quand je serai libre, je résoudrai.

Commented by Ar Brandon last updated on 15/Oct/20

D'accord, merci

Answered by Bird last updated on 15/Oct/20

$$I={\int }_0^{\mathrm{\infty }}\frac{x^2-2}{x^4+x^2+1}dx\Rightarrow$$$$I=\frac{1}{2}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{x^2-2}{x^4+x^2+1}dx$$$$let\phi \left(z\right)=\frac{z^2-2}{z^4+z^2+1}polesof\phi ?$$$$z^4+z^2+1=0\Rightarrow u^2+u+1=0(u=z^{2)}$$$$\mathrm{\Delta }=-3\Rightarrow u_1=\frac{-1+i\sqrt{3}}{2}=e^{\frac{i2\pi }{3}}$$$$u_2=e^{-\frac{i2\pi }{3}}$$$$\Rightarrow \phi \left(z\right)=\frac{z^2-2}{(z^2-e^{\frac{i2\pi }{3}})(z^2-e^{-\frac{i2\pi }{3}})}$$$$=\frac{z^2-2}{(z-e^{\frac{i\pi }{3}})(z+e^{\frac{i\pi }{3}})(z-e^{-\frac{i\pi }{3}})(z+e^{-\frac{i\pi }{3}})}$$$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\phi \left(z\right)dz=2i\pi \{Res(\phi ,e^{\frac{i\pi }{3}})+Res(\phi ,-e^{-\frac{i\pi }{3}})\}$$$$Res(\phi ,e^{\frac{i\pi }{3}})=\frac{e^{\frac{2i\pi }{3}}-2}{2e^{\frac{i\pi }{3}}\left(2isin\left(\frac{2\pi }{3}\right)\right)}$$$$=\frac{1}{2i\sqrt{3}}(e^{\frac{i\pi }{3}}-2e^{-\frac{i\pi }{3}})$$$$Res(\phi ,-e^{-\frac{i\pi }{3}})=\frac{e^{-\frac{2i\pi }{3}}-2}{(-2e^{-\frac{i\pi }{3}})(-2isin\left(\frac{2\pi }{3}\right)}$$$$=\frac{e^{-\frac{i\pi }{3}}-2e^{\frac{i\pi }{3}}}{2i\sqrt{3}}\Rightarrow$$$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\phi \left(z\right)dz=\frac{2i\pi }{2i\sqrt{3}}\{e^{\frac{i\pi }{3}}-2e^{-\frac{i\pi }{3}}+e^{-\frac{i\pi }{3}}-2e^{\frac{i\pi }{3}}\}$$$$=\frac{\pi }{\sqrt{3}}\{-e^{\frac{i\pi }{3}}-e^{-\frac{i\pi }{3}}\}$$$$=-\frac{\pi }{\sqrt{3}}\left(2cos\left(\frac{\pi }{3}\right)\right)=-\frac{\pi }{\sqrt{3}}\Rightarrow$$$$I=-\frac{\pi }{2\sqrt{3}}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com