Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 118073 by bemath last updated on 15/Oct/20

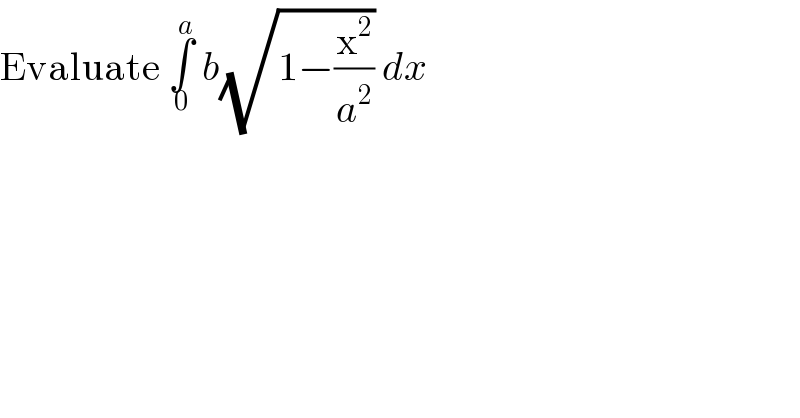
Evaluate ∫_0 ^a b(√(1−(x^2 /a^2 ))) dx

$$\mathrm{Evaluate}\:\underset{\mathrm{0}} {\overset{{a}} {\int}}\:{b}\sqrt{\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\:{dx}\: \\ $$

Answered by john santu last updated on 15/Oct/20

I=∫_0 ^a (b/a) (√(a^2 −x^2 )) dx ; the integral represents the area of a quarter circle having radius a I= (b/a)×(1/4)πa^2 = ((πab)/4)

$${I}=\underset{\mathrm{0}} {\overset{{a}} {\int}}\:\frac{{b}}{{a}}\:\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:{dx}\:;\:{the}\:{integral}\:{represents}\:{the}\:{area} \\ $$$${of}\:{a}\:{quarter}\:{circle}\:{having}\:{radius}\:{a} \\ $$$${I}=\:\frac{{b}}{{a}}×\frac{\mathrm{1}}{\mathrm{4}}\pi{a}^{\mathrm{2}} \:=\:\frac{\pi{ab}}{\mathrm{4}} \\ $$

Commented by bemath last updated on 15/Oct/20

gave kudos

$$\mathrm{gave}\:\mathrm{kudos} \\ $$

Commented by MJS_new last updated on 15/Oct/20

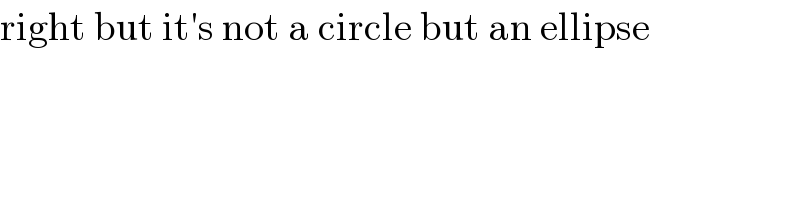
right but it′s not a circle but an ellipse

$$\mathrm{right}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{but}\:\mathrm{an}\:\mathrm{ellipse} \\ $$

Commented by john santu last updated on 16/Oct/20

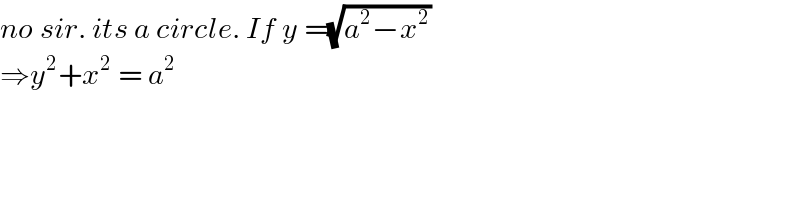
no sir. its a circle. If y =(√(a^2 −x^2 )) ⇒y^2 +x^2 = a^2

$${no}\:{sir}.\:{its}\:{a}\:{circle}.\:{If}\:{y}\:=\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\: \\ $$$$\Rightarrow{y}^{\mathrm{2}} +{x}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} \: \\ $$

Commented by MJS_new last updated on 16/Oct/20

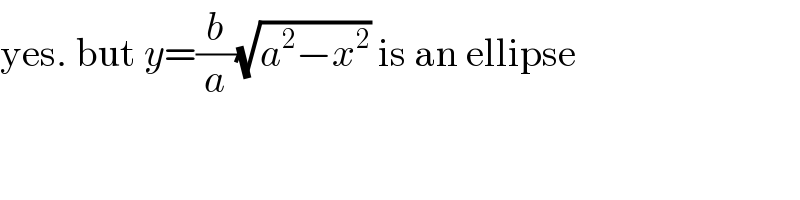
yes. but y=(b/a)(√(a^2 −x^2 )) is an ellipse

$$\mathrm{yes}.\:\mathrm{but}\:{y}=\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{an}\:\mathrm{ellipse} \\ $$

Answered by 1549442205PVT last updated on 15/Oct/20

Evaluate ∫_0 ^a b(√(1−(x^2 /a^2 ))) dx Put x=acosϕ(ϕ∈[0,π])⇒dx=−asinϕdϕ I=−∫_(π/2) ^( 0) absin^2 ϕdϕ=∫_0 ^( π/2) ab((1−cos2ϕ)/2)dϕ =(((abϕ)/2)−((ab)/4)sin2ϕ)∣_0 ^(π/2) =((abπ)/( 4))

$$\mathrm{Evaluate}\:\underset{\mathrm{0}} {\overset{{a}} {\int}}\:{b}\sqrt{\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\:{dx}\: \\ $$$$\mathrm{Put}\:\mathrm{x}=\mathrm{acos}\varphi\left(\varphi\in\left[\mathrm{0},\pi\right]\right)\Rightarrow\mathrm{dx}=−\mathrm{asin}\varphi\mathrm{d}\varphi \\ $$$$\mathrm{I}=−\int_{\pi/\mathrm{2}} ^{\:\mathrm{0}} \mathrm{absin}^{\mathrm{2}} \varphi\mathrm{d}\varphi=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{ab}\frac{\mathrm{1}−\mathrm{cos2}\varphi}{\mathrm{2}}\mathrm{d}\varphi \\ $$$$=\left(\frac{\mathrm{ab}\varphi}{\mathrm{2}}−\frac{\mathrm{ab}}{\mathrm{4}}\mathrm{sin2}\varphi\right)\mid_{\mathrm{0}} ^{\pi/\mathrm{2}} =\frac{\mathrm{ab}\pi}{\:\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com