
Question and Answers Forum
Question Number 118078 by bemath last updated on 15/Oct/20
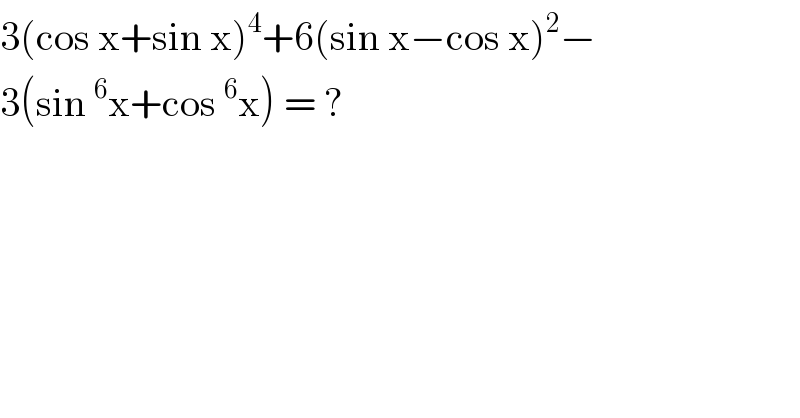
Answered by bobhans last updated on 15/Oct/20
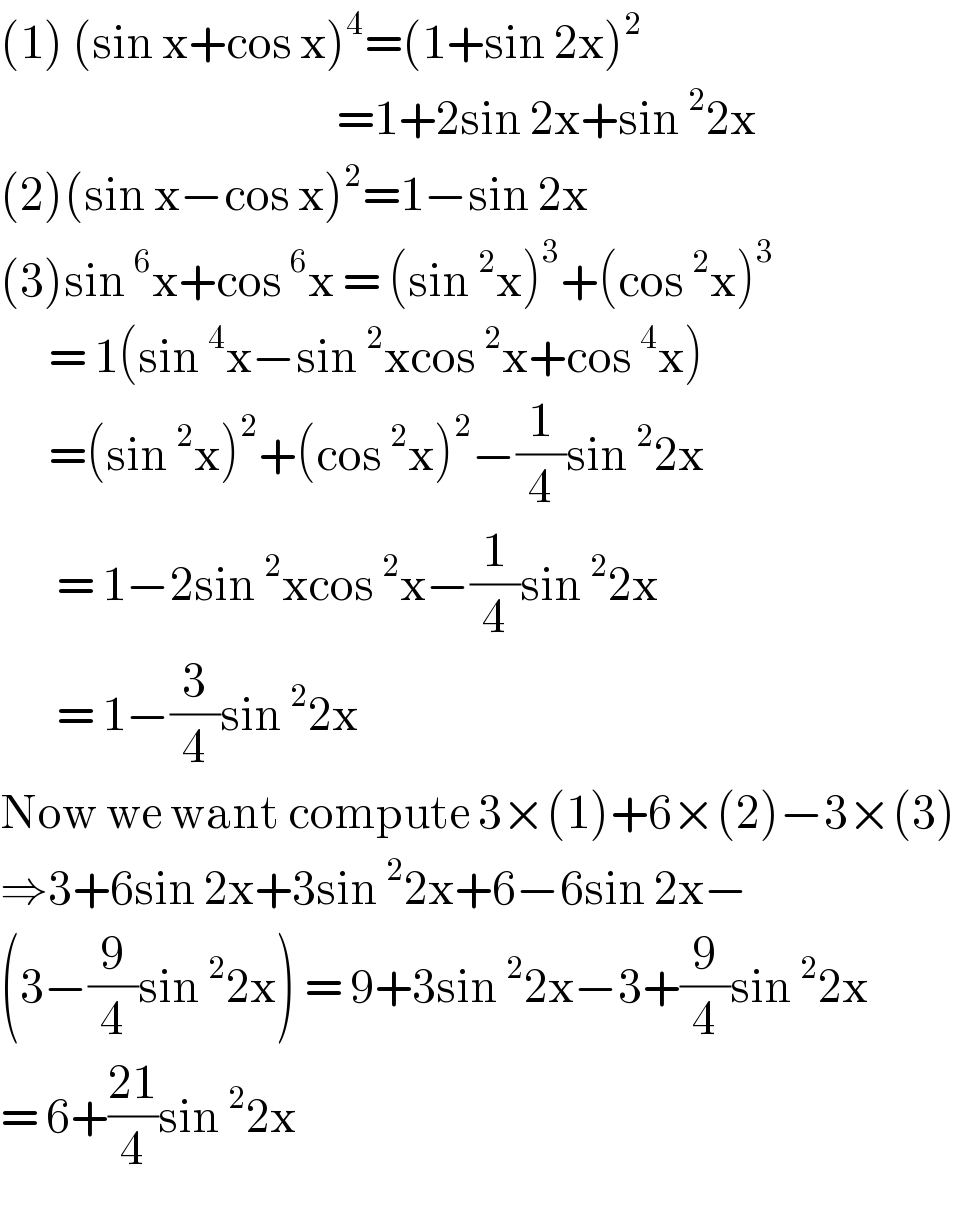
Answered by MJS_new last updated on 15/Oct/20
![3(c+s)^4 +6(s−c)^2 −3(s^6 +c^6 )= =−3(c^6 +s^6 −c^4 −s^4 −4c^3 s−4cs^3 −6c^2 s^2 −2c^2 −2s^2 +4cs)= [c=(√(1−s^2 ))] =−3(7(s^4 −s^2 )−2)= =3(7s^2 (1−s^2 )+2)= =3(7s^2 c^2 +2)= =6+21sin^2 x cos^2 x = =6+((21)/4)sin^2 2x = =((69)/8)−((21)/8)cos 4x](Q118096.png)
Commented by bemath last updated on 15/Oct/20

| ||
Question and Answers Forum | ||
Question Number 118078 by bemath last updated on 15/Oct/20 | ||
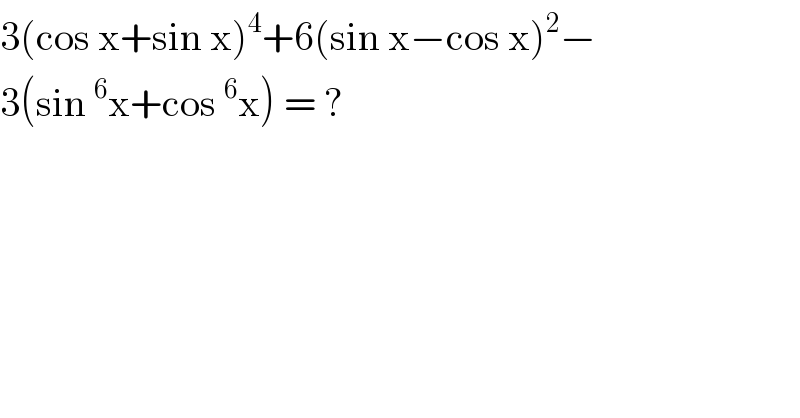 | ||
Answered by bobhans last updated on 15/Oct/20 | ||
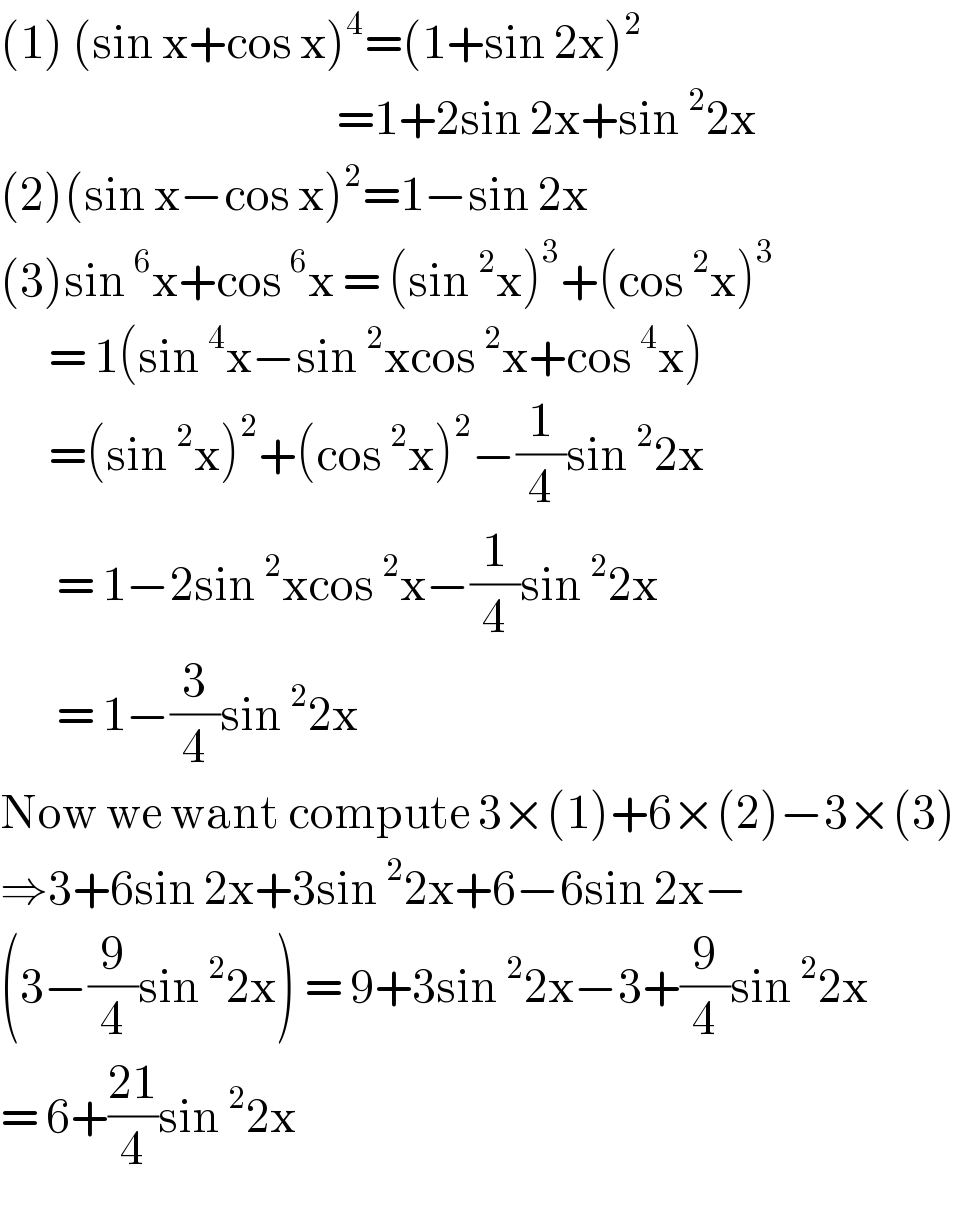 | ||
| ||
Answered by MJS_new last updated on 15/Oct/20 | ||
![3(c+s)^4 +6(s−c)^2 −3(s^6 +c^6 )= =−3(c^6 +s^6 −c^4 −s^4 −4c^3 s−4cs^3 −6c^2 s^2 −2c^2 −2s^2 +4cs)= [c=(√(1−s^2 ))] =−3(7(s^4 −s^2 )−2)= =3(7s^2 (1−s^2 )+2)= =3(7s^2 c^2 +2)= =6+21sin^2 x cos^2 x = =6+((21)/4)sin^2 2x = =((69)/8)−((21)/8)cos 4x](Q118096.png) | ||
| ||
Commented by bemath last updated on 15/Oct/20 | ||
 | ||